knight's tour hamiltonian cycle

• Mission and Vision
• Annual Reports
• Complaints Procedures
• Delegates Information
• Executive Board
• Staff/Contact Us
• Requests for Proposals (RFP)
• Job Postings
• Guide to a Successful Chess Club
• The Ratings System
• New to National Events Guide
• Safe Play Policy
• How to Send an Email Blast
• Guide to Scholastic Chess
• Accessibility Guidelines
• Our Initiative
• Top 100 Lists
• Olympiad Campaign
• At-Risk Youth
• Correspondence Chess
• 2023-24 Scholastic Regulations
• Scholastic Council Members
• Chess Life Kids Online
• Faces of US Chess
• Our Heritage: Yearbook
• Upcoming Events
• Grants/Awards
• Spectator Policy at Scholastics
• Current Scholastic Regulations
• Event Bidding
• Official Rules
• Plan Ahead Calendar
• Grand Prix Information
• Pan American Youth Championships
• Pan Am Youth Champ
• Irwin: Seniors (50+)
• Denker: HS (9-12)
• Haring: Girls (K-12)
• Barber: MS (6-8)
• Rockefeller: ES (K-5)
• Weeramantry: Blitz
• Player/Ratings Look-Up
• Past Event Crosstables
• Events Rated List
• TD/Affiliate Support
• Club/Affiliate Search
• Rating System Algorithm
• MSA/Ratings FAQ
• Become a Member
• Become an Affiliate
• Redeem a Voucher
• Benefactor Members
• Membership Form PDF
• Info for Members/Affiliates
• Donor Bill of Rights
• Giving Tuesday
• Donate Online
• Case for Support
• At-Risk-Youth

Chess and Math: A Closer Look at the Knight's Tour

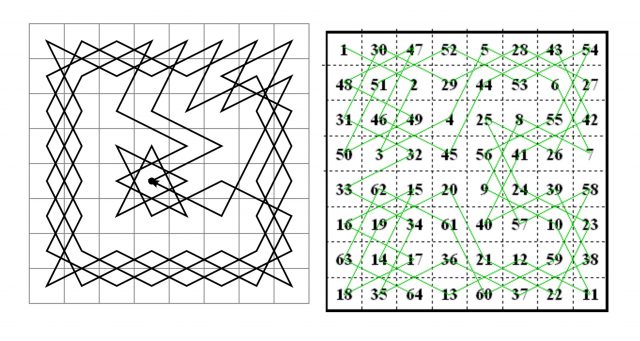
• April 2024 (24)
• March 2024 (34)
• February 2024 (25)
• January 2024 (26)
• December 2023 (29)
• November 2023 (26)
• October 2023 (38)
• September 2023 (27)
• August 2023 (37)
• July 2023 (47)
• June 2023 (33)
• May 2023 (37)
• April 2023 (45)
• March 2023 (37)
• February 2023 (28)
• January 2023 (31)
• December 2022 (23)
• November 2022 (32)
• October 2022 (31)
• September 2022 (19)
• August 2022 (39)
• July 2022 (32)
• June 2022 (35)
• May 2022 (21)
• April 2022 (31)
• March 2022 (33)
• February 2022 (21)
• January 2022 (27)
• December 2021 (36)
• November 2021 (34)
• October 2021 (25)
• September 2021 (25)
• August 2021 (41)
• July 2021 (36)
• June 2021 (29)
• May 2021 (29)
• April 2021 (31)
• March 2021 (33)
• February 2021 (28)
• January 2021 (29)
• December 2020 (38)
• November 2020 (40)
• October 2020 (41)
• September 2020 (35)
• August 2020 (38)
• July 2020 (36)
• June 2020 (46)
• May 2020 (42)
• April 2020 (37)
• March 2020 (60)
• February 2020 (39)
• January 2020 (45)
• December 2019 (36)
• November 2019 (35)
• October 2019 (42)
• September 2019 (45)
• August 2019 (56)
• July 2019 (44)
• June 2019 (35)
• May 2019 (40)
• April 2019 (48)
• March 2019 (61)
• February 2019 (39)
• January 2019 (30)
• December 2018 (29)
• November 2018 (51)
• October 2018 (45)
• September 2018 (29)
• August 2018 (49)
• July 2018 (35)
• June 2018 (31)
• May 2018 (39)
• April 2018 (31)
• March 2018 (26)
• February 2018 (33)
• January 2018 (30)
• December 2017 (26)
• November 2017 (24)
• October 2017 (30)
• September 2017 (30)
• August 2017 (32)
• July 2017 (27)
• June 2017 (32)
• May 2017 (26)
• April 2017 (37)
• March 2017 (28)
• February 2017 (30)
• January 2017 (27)
• December 2016 (29)
• November 2016 (24)
• October 2016 (32)
• September 2016 (31)
• August 2016 (27)
• July 2016 (24)
• June 2016 (26)
• May 2016 (19)
• April 2016 (30)
• March 2016 (37)
• February 2016 (27)
• January 2016 (33)
• December 2015 (25)
• November 2015 (23)
• October 2015 (16)
• September 2015 (28)
• August 2015 (28)
• July 2015 (6)
• June 2015 (1)
• May 2015 (2)
• April 2015 (1)
• February 2015 (3)
• January 2015 (1)
• December 2014 (1)
• July 2010 (1)
• October 1991 (1)
• August 1989 (1)
• January 1988 (1)
• December 1983 (1)

Announcements

• The Herbert B. Jacklyn Program is Open For 2024-25 Submissions »
• 2024 Scholar-Chessplayer Awards Announced: Six Players Honored at the 2024 National High School Championship »
• US Chess Safe Play Guide for Tournament Directors, Organizers, and Participants Now Available »
• 2024 North American Junior Championships Announced »

US CHESS PRESS

Knight Graph

Knight graphs are bipartite and therefore are perfect .

The following table summarizes some named graph complements of knight graphs.

(E. Weisstein, Nov. 16, 2014).

The following table extends and corrects some additional results given by Kraitchik (1942, pp. 264-265). Here, DHP means geometrically distinct Hamiltonian paths, DSHP means geometrically distinct symmetric paths, HP means total (directed) Hamiltonian paths, DHC means geometrically distinct Hamiltonian cycles, and HC means total (directed) Hamiltonian cycles.

with corresponding closed-form generating function

This result was obtained independently by D. E. Knuth and N. D. Elkies in April 1994, both using the so-called transfer-matrix method (Stanley 1999, Ch. 4.7; Elkies and Stanley 2003).

Explore with Wolfram|Alpha

More things to try:

• Archimedean solids
• Fresnel S(x) integral rep
• int e^t sin(5t) dt

Cite this as:

Weisstein, Eric W. "Knight Graph." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/KnightGraph.html

Subject classifications

• Contract bridge
• Connection games
• Cards classifier
• List of dice games
• Rummy games
• Chess World Cup
• FIDE Grand Prix
• World Championship
• List of strong tournaments
• List of world championships
• Checkmate patterns
• Chess openings
• Chess strategy
• Chess tactics
• Chess theory
• Pawn structure
• Problems/Compositions
• Computer chess
• Chess engines
• Chess software
• Cheating in chess
• Chess prodigy
• List of Grandmasters
• Grandmasters by country
• Top player comparison
• World rankings
• Chess titles
• Rating systems
• Correspondence chess
• List of chess variants
• Rules of chess
• Chess notation
• Outline of chess
• Timeline of chess

Knight's tour

A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed , otherwise it is open .

The knight's tour problem is the mathematical problem of finding a knight's tour. Creating a program to find a knight's tour is a common problem given to computer science students. Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 x 8, as well as irregular (non-rectangular) boards.

The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight's tour problem can be solved in linear time.

The earliest known reference to the knight's tour problem dates back to the 9th century AD. In Rudraṭa's Kavyalankara (5.15), a Sanskrit work on Poetics, the pattern of a knight's tour on a half-board has been presented as an elaborate poetic figure ("citra-alaṅkāra") called the "turagapadabandha" or 'arrangement in the steps of a horse.' The same verse in four lines of eight syllables each can be read from left to right or by following the path of the knight on tour. Since the Indic writing systems used for Sanskrit are syllabic, each syllable can be thought of as representing a square on a chess board. Rudrata's example is as follows:

से ना ली ली ली ना ना ना ली

ली ना ना ना ना ली ली ली ली

न ली ना ली ली ले ना ली ना

ली ली ली ना ना ना ना ना ली

se nā lī lī lī nā nā lī

lī nā nā nā nā lī lī lī

na lī nā lī le nā lī nā

lī lī lī nā nā nā nā lī

For example, the first line can be read from left to right or by moving from the first square to second line, third syllable (2.3) and then to 1.5 to 2.7 to 4.8 to 3.6 to 4.4 to 3.2.

One of the first mathematicians to investigate the knight's tour was Leonhard Euler. The first procedure for completing the Knight's Tour was Warnsdorf's rule, first described in 1823 by H. C. von Warnsdorf.

In the 20th century, the Oulipo group of writers used it among many others. The most notable example is the 10 x 10 Knight's Tour which sets the order of the chapters in Georges Perec's novel Life: A User's Manual . The sixth game of the 2010 World Chess Championship between Viswanathan Anand and Veselin Topalov saw Anand making 13 consecutive knight moves (albeit using both knights); online commentors jested that Anand was trying to solve the Knight's Tour problem during the game.

Schwenk proved that for any m x n board with m ≤ n , a closed knight's tour is always possible unless one or more of these three conditions are met:

• m and n are both odd
• m = 1, 2, or 4
• m = 3 and n = 4, 6, or 8.

Cull et al. and Conrad et al. proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight's tour.

Number of tours

On an 8 x 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately, as are rotations and reflections). The number of undirected closed tours is half this number, since every tour can be traced in reverse. There are 9,862 undirected closed tours on a 6 x 6 board.

Finding tours with computers

There are quite a number of ways to find a knight's tour on a given board with a computer. Some of these methods are algorithms while others are heuristics.

Brute force algorithms

A brute-force search for a knight's tour is impractical on all but the smallest boards; for example, on an 8x8 board there are approximately 4x10 51 possible move sequences, and it is well beyond the capacity of modern computers (or networks of computers) to perform operations on such a large set. However the size of this number gives a misleading impression of the difficulty of the problem, which can be solved "by using human insight and ingenuity ... without much difficulty."

Divide and conquer algorithms

By dividing the board into smaller pieces, constructing tours on each piece, and patching the pieces together, one can construct tours on most rectangular boards in polynomial time.

Neural network solutions

The Knight's Tour problem also lends itself to being solved by a neural network implementation. The network is set up such that every legal knight's move is represented by a neuron, and each neuron is initialized randomly to be either "active" or "inactive" (output of 1 or 0), with 1 implying that the neuron is part of the final solution. Each neuron also has a state function (described below) which is initialized to 0.

When the network is allowed to run, each neuron can change its state and output based on the states and outputs of its neighbors (those exactly one knight's move away) according to the following transition rules:

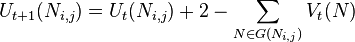
Warnsdorff's rule

Warnsdorff's rule is a heuristic for finding a knight's tour. We move the knight so that we always proceed to the square from which the knight will have the fewest onward moves. When calculating the number of onward moves for each candidate square, we do not count moves that revisit any square already visited. It is, of course, possible to have two or more choices for which the number of onward moves is equal; there are various methods for breaking such ties, including one devised by Pohl and another by Squirrel and Cull.

This rule may also more generally be applied to any graph. In graph-theoretic terms, each move is made to the adjacent vertex with the least degree. Although the Hamiltonian path problem is NP-hard in general, on many graphs that occur in practice this heuristic is able to successfully locate a solution in linear time. The knight's tour is a special case.

The heuristic was first described in "Des Rösselsprungs einfachste und allgemeinste Lösung" by H. C. von Warnsdorff in 1823. A computer program that finds a Knight's Tour for any starting position using Warnsdorff's rule can be found in the book 'Century/Acorn User Book of Computer Puzzles' edited by Simon Dally (ISBN 071260541X).

• Abu-Bakr Muhammad ben Yahya as-Suli
• George Koltanowski
• Longest uncrossed knight's path
• Eight queens puzzle

What is the Knight’s Tour problem?

Answered by Michael Weatherspoon

The Knight’s Tour problem is a fascinating puzzle that has intrigued chess enthusiasts and mathematicians for centuries. As a chess grandmaster, I have encountered this problem numerous times and have marveled at its complexity. Allow me to explain in detail what the Knight’s Tour problem entails and why it has captured the imagination of many.

At its core, the Knight’s Tour problem is a variation of the general Hamiltonian path problem in graph theory. In simpler terms, it involves finding a sequence of moves for a knight on a chessboard such that the knight visits every square exactly once. The knight follows the standard moves of a knight in chess, which means it can move in an L-shape, either two squares horizontally and one square vertically or two squares vertically and one square horizontally.

The objective of the Knight’s Tour problem can be twofold. Firstly, one can aim to find an open tour, where the knight starts on one square and ends on another, without revisiting any square in between. Secondly, one can strive to find a closed tour, where the knight starts and ends on the same square, forming a closed loop on the chessboard. While finding an open tour is challenging enough, finding a closed tour is even more difficult and is equivalent to solving the Hamiltonian cycle problem.

The allure of the Knight’s Tour problem lies in its seemingly simple premise but its intricate nature. It appears as a straightforward task to navigate the knight across the chessboard, but as the board size increases, the complexity grows exponentially. The number of possible knight’s tours on an n x n chessboard is immense, making it a true test of problem-solving skills and mathematical insight.

To better understand the intricacies of the Knight’s Tour problem, let’s delve into its connection with the Hamiltonian path problem. The Hamiltonian path problem involves finding a path that visits every vertex of a graph exactly once. In the context of the chessboard, each square represents a vertex, and the knight’s moves correspond to the edges of the graph. Thus, finding a Knight’s Tour is essentially finding a Hamiltonian path on a modified chessboard graph.

Interestingly, unlike the general Hamiltonian path problem, the Knight’s Tour problem can be solved in linear time. This means that as the chessboard size increases, the time required to find a solution does not grow exponentially. However, this does not imply that finding a Knight’s Tour is easy or trivial. The efficient algorithms developed for solving the Knight’s Tour problem utilize various heuristics and optimizations to minimize the computational complexity.

In my personal experience as a chess grandmaster, I have encountered the Knight’s Tour problem in various contexts. It has been a topic of discussion among fellow chess players, a challenge in puzzle books and magazines, and even a source of inspiration for artistic interpretations. Solving the Knight’s Tour not only requires logical thinking and strategic planning but also a deep understanding of the knight’s movement patterns.

The Knight’s Tour problem is a captivating puzzle that involves finding a sequence of moves for a knight on a chessboard such that it visits every square exactly once. It is a variation of the Hamiltonian path problem and can be approached with the objective of finding an open or closed tour. While the problem can be solved in linear time, its complexity grows exponentially with the chessboard size. As a chess grandmaster, I have come to appreciate the intricate nature of the Knight’s Tour problem and its ability to challenge and captivate the minds of chess enthusiasts and mathematicians alike.

Related posts:

12.7 Hamilton Cycles

Learning objectives.

After completing this section, you should be able to:

• Describe and identify Hamilton cycles.
• Compute the number of Hamilton cycles in a complete graph.
• Apply and evaluate weighted graphs.

In Euler Circuits and Euler Trails , we looked for circuits and paths that visited each edge of a graph exactly once. In this section, we will look for circuits that visit each vertex exactly once. Like many concepts in graph theory, the idea of a circuit that visits each vertex once was inspired by games and puzzles. As early as the 9th century, Indian and Islamic intellectuals wondered whether it was possible for a knight to visit every space on a chess board of a given size, which is equivalent to visiting every vertex of a graph that represents the chess board.

In 1857, a mathematician named William Rowan Hamilton invented a puzzle in which players were asked to find a route along the edges of a dodecahedron (see Figure 12.156 ), which visited every vertex exactly once. Let’s explore how graph theory provides insight into these games as well as practical applications such as the Traveling Salesperson Problem.

Hamilton’s Puzzle

Before we look at the solution to Hamilton's puzzle, let’s review some vocabulary we used in Figure 12.157 . It will be helpful to remember that directed cycle is a type of circuit that doesn’t repeat any edges or vertices.

The goal of Hamilton's puzzle was to find a route along the edges of the dodecahedron, which visits each vertex exactly once. A dodecahedron is a three-dimensional space figure with faces that are all pentagons as we saw in Figure 12.156 .

Since it is easier to visualize two dimensions rather than three, we will flatten out the dodecahedron and look at the edges and vertices on a flat surface. Graph A in Figure 12.158 shows a two-dimensional graph of the edges and vertices, and Graph B shows an untangled version of Graph A in which no edges are crossing. Graph B in Figure 12.158 is very similar to the design of the game board that Hamilton invented for his puzzle.

We can see that this is a planar graph because it can be “untangled.” In order to solve Hamilton’s puzzle, we need to find a circuit that visits every vertex once. A solution is shown in Figure 12.159 .

A circuit that doesn’t repeat any vertices, like the one in Figure 12.159 , is called a directed cycle. So, we can most accurately say that Hamilton’s puzzle asks us to find a directed cycle that visits every vertex in a graph exactly once. Because Hamilton created and solved this puzzle, these special circuits were named Hamilton cycles , or Hamilton circuits .

Icosian Game

When Hamilton invented his puzzle in the 19th century, it was originally called the Icosian game. This was a reference to an icosahedron, not a dodecahedron. Why? Hamilton was actually interested in the symmetries of icosahedrons. It turns out that these two space figures are related to each other. The dodecahedron has 30 edges, 20 faces, and 12 vertices, while the icosahedron has 30 edges, 12 faces, and 20 vertices. By relating the vertices of the dodecahedron to the faces of the icosahedron, Hamilton was able to make the mathematical connections necessary to use graph theory and dodecahedrons to make discoveries about the symmetries of icosahedrons.

Hamilton Cycles vs. Euler Circuits

Let’s practice naming and identifying Hamilton cycles, as well as distinguishing them from Euler circuits. It is important to remember that Euler circuits visit all edges without repetition, while Hamilton cycles visit all vertices without repetition. Hamilton cycles are named by their vertices just like all circuits. An example is given in Figure 12.160 .

Notice that the Hamilton cycle a → b → c → d for Graph Z in Figure 12.160 is NOT an Euler circuit, because it does not visit edge ac ac . Some Hamilton cycles are also Euler circuits while some are not, and some Euler circuits are Hamilton cycles while some are not.

TIP! Sometimes students confuse Euler circuits with Hamilton cycles. To help you remember, think of the E in Euler as standing for Edge.

Example 12.33

Differentiating between hamilton cycles or euler circuits.

Use Figure 12.161 to determine whether the given circuit is a Hamilton cycle, an Euler circuit, both, or neither.

• a → b → c → e → h → g → f → d → a
• g → e → h → g → f → d → a → b → d → g
• a → b → c → e → h → g → f → d → b → e → g → d → a
• This circuit is a Hamilton cycle only. It visits each vertex exactly once, so, it is a Hamilton cycle. It is not an Euler circuit because it doesn’t visit all of the edges.
• This circuit is neither Hamilton cycle nor an Euler circuit. It doesn’t visit vertex c c , so, it is not a Hamilton cycle. It also doesn’t visit edges be be and ce ce , so, it is not an Euler circuit.
• This circuit is an Euler circuit only. It visits several vertices more than once; so, it is not a Hamilton cycle. It visits every edge exactly once, so, it is an Euler circuit.

TIP! Euler circuits never skip a vertex, so, they only fail to be Hamilton cycles when they visit a vertex more than once. Hamilton cycles never visit any edges twice, so, they only fail to be Euler circuits when they skip edges.

Your Turn 12.33

Notice that the graph is a cycle. A cycle will always be Eulerian because all vertices are degree 2. Moreover, any circuit in the graph will always be both an Euler circuit and a Hamilton cycle. It is not always as easy to determine if a graph has a Hamilton cycle as it is to see that it has an Euler circuit, but there is a large group of graphs that we know will always have Hamilton cycles, the complete graphs. Since all vertices in a complete graph are adjacent, we can always find a directed cycle that visits all the vertices. For example, look at the directed six-cycle, n → o → p → q → r → s , in the complete graph with six vertices in Figure 12.162 .

That is not the only directed six-cycle in the graph though. We could find another just be reversing the direction, and we could find even more by using different edges. So, how many Hamilton cycles are in a complete graph with n n vertices? Before we tackle this problem, let’s look at a shorthand notation that we use in mathematics which will be helpful to us.

In many areas of mathematics, we must calculate products like 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 or 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 , products that involve multiplying all the counting numbers from a particular number down to 1. Imagine that the product happened to be all the numbers from 100 down to 1. That’s a lot of writing! Instead of writing all of that out, mathematicians came up with a shorthand notation. For example, instead of 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 , we write 7 ! 7 ! , which is read “7 factorial .” In other words, the product of all the counting numbers from n n down to 1 is called n n factorial and it is written n ! n !

Example 12.34

Evaluating factorials.

Evaluate n ! n ! and ( n − 1 ) ! ( n − 1 ) ! for n = 4 n = 4 .

n ! = 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 n ! = 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 and ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ! = 3 ⋅ 2 ⋅ 1 = 6 ( n − 1 ) ! = ( 4 − 1 ) ! = 3 ! = 3 ⋅ 2 ⋅ 1 = 6

Your Turn 12.34

A common use for factorials is counting the number of ways to arrange objects. Suppose that there were three students, Aryana, Byron, and Carlos, who wanted to line up in a row. How many arrangements are possible? There are six possibilities: ABC, ACB, BAC, BCA, CAB, or CBA. Notice that there were three students being arranged, and the number of possible arrangements is three.

The number of ways to arrange n n distinct objects is n ! n ! .

Example 12.35

Counting arrangements of letters.

Find the number of ways to arrange the letters a, b, c, and d.

4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

Your Turn 12.35

Counting hamilton cycles in complete graphs.

Now, let’s get back to answering the question of how many Hamilton cycles are in a complete graph. In Table 12.8 , we have drawn all the four cycles in a complete graph with four vertices. Remember, cycles can be named starting with any vertex in the cycle, but we will name them starting with vertex a a .

Table 12.8 shows that there are three unique four-cycles in a complete graph with four vertices. Notice that there were two ways to name each cycle, one reading the vertices in a clockwise direction and one reading the vertices in a counterclockwise direction. This is important to us because we are interested in Hamilton cycles, which are directed cycles. Although the cycles (a, b, c, d) and (a, d, c, b) are the same cycle, the directed cycles, a → b → c → d → a and a → d → c → b → a , which travel the same route in reverse order are considered different directed cycles, as shown in Table 12.9 .

The six directed four-cycles in Table 12.9 are the only distinct Hamilton cycles in a complete graph with four vertices. Six is also the number of ways to arrange the three letters b, c, and d. (Do you see why?) The number of ways to arrange three letters is 3 ! = 3 ⋅ 2 ⋅ 1 = 6 3 ! = 3 ⋅ 2 ⋅ 1 = 6 . Similarly, the number of Hamilton cycles in a graph with five vertices is the number of ways to arrange four letters, which is 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 . In general, to find the number of Hamilton cycles in a graph, we take one less than the number of vertices and find its factorial.

The number of distinct Hamilton cycles in a complete graph with n n vertices is ( n − 1 ) ! ( n − 1 ) !

Example 12.36

Counting hamilton cycles in a complete graph.

How many Hamilton cycles are in the complete graph in Figure 12.163 ?

There are five vertices in the graph. Using n = 5 n = 5 , we have ( n − 1 ) ! = ( 5 − 1 ) ! = 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 ( n − 1 ) ! = ( 5 − 1 ) ! = 4 ! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 Hamilton cycles.

Your Turn 12.36

Weighted graphs.

Suppose that an officer in the U.S. Air Force who is stationed at Vandenberg Air Force base must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needs to visit each base once. The vertices in the graph in Figure 12.164 represent the four U.S. Air Force bases, Vandenberg, Edwards, Los Angeles, and Beale. The edges are labeled to with the driving distance between each pair of cities.

The graph in Figure 12.164 is called a weighted graph , because each edge has been assigned a value or weight. The weights can represent quantities such as time, distance, money, or any quantity associated with the adjacent vertices joined by the edges. The total weight of any walk, trail, or path is the sum of the weights of the edges it visits.

Notice that the officer’s trip can be represented as a Hamilton cycle, because each of the four vertices in the graph is visited exactly once.

Example 12.37

Finding hamilton cycles of lowest weight.

Use Figure 12.164 and the given Hamilton cycles to answer the following questions.

V → L → E → B → V

V → L → B → E → V

V → E → L → B → V

V → B → E → L → V

• Which of the Hamilton cycles (directed cycles) lie on the same cycle (undirected cycle) in the graph?
• Find the total weight of each cycle.
• Of the four, which of the Hamilton cycles describes the shortest trip for the officer? Describe the route.
• V → L → E → B → V and V → B → E → L → V follow the same edges in reverse order.

V → L → E → B → V and V → B → E → L → V each have total weight 159 + 106 + 410 + 396 = 1071 159 + 106 + 410 + 396 = 1071 .

V → L → B → E → V has a total weight 159 + 439 + 410 + 207 = 1215 159 + 439 + 410 + 207 = 1215 .

V → E → L → B → V has a total weight 396 + 439 + 106 + 207 = 1148 396 + 439 + 106 + 207 = 1148 .

• Hamilton cycles V → L → E → B → V and V → B → E → L → V each have the lowest total weight. The officer would take the route from Vandenberg, to Los Angeles, to Edwards, to Beale, and back to Vandenberg, or reverse that route.

Your Turn 12.37

Check your understanding, section 12.7 exercises.

• b → a → c → d → b
• b → a → d → c → b
• b → c → a → d → b
• b → c → d → a → b
• b → d → a → c → b
• b → d → c → a → b
• i → f → g → h → e → i
• i → f → g → e → h → i
• i → f → h → g → e → i
• i → f → h → e → g → i
• i → f → e → g → h → i
• i → f → e → h → g → i
• i → g → f → h → e → i
• i → g → f → e → h → i
• i → g → h → f → e → i
• i → g → h → e → f → i
• i → g → e → f → h → i
• i → g → e → h → f → i
• i → h → g → f → e → i
• i → h → g → e → f → i
• i → h → f → g → e → i
• i → h → f → e → g → i
• i → h → e → g → f → i
• i → h → e → f → g → i
• i → e → g → h → f → i
• i → e → g → f → h → i
• i → e → h → g → f → i
• i → e → h → f → g → i
• i → e → f → g → h → i
• i → e → f → h → g → i

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/12-7-hamilton-cycles

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Practice Backtracking
• Interview Problems on Backtracking
• MCQs on Backtracking
• Tutorial on Backtracking
• Backtracking vs Recursion
• Backtracking vs Branch & Bound
• Print Permutations
• Subset Sum Problem
• N-Queen Problem
• Knight's Tour
• Sudoku Solver
• Rat in Maze
• Hamiltonian Cycle
• Graph Coloring
• Backtracking Algorithm
• Introduction to Backtracking - Data Structure and Algorithm Tutorials
• Difference between Backtracking and Branch-N-Bound technique
• What is the difference between Backtracking and Recursion?

Standard problems on backtracking

• The Knight's tour problem
• Rat in a Maze
• N Queen Problem
• Subset Sum Problem using Backtracking
• M-Coloring Problem
• Algorithm to Solve Sudoku | Sudoku Solver
• Magnet Puzzle
• Remove Invalid Parentheses
• A backtracking approach to generate n bit Gray Codes
• Permutations of given String

Easy Problems on Backtracking

• Print all subsets of a given Set or Array
• Check if a given string is sum-string
• Count all possible Paths between two Vertices
• Find all distinct subsets of a given set using BitMasking Approach
• Find if there is a path of more than k length from a source
• Print all paths from a given source to a destination
• Print all possible strings that can be made by placing spaces

Medium prblems on Backtracking

• 8 queen problem
• Combinational Sum
• Warnsdorff's algorithm for Knight’s tour problem
• Find paths from corner cell to middle cell in maze
• Find Maximum number possible by doing at-most K swaps
• Rat in a Maze with multiple steps or jump allowed
• N Queen in O(n) space

Hard problems on Backtracking

• Power Set in Lexicographic order
• Word Break Problem using Backtracking
• Partition of a set into K subsets with equal sum
• Longest Possible Route in a Matrix with Hurdles
• Find shortest safe route in a path with landmines
• Printing all solutions in N-Queen Problem
• Print all longest common sub-sequences in lexicographical order
• Top 20 Backtracking Algorithm Interview Questions

Warnsdorff’s algorithm for Knight’s tour problem

Problem : A knight is placed on the first block of an empty board and, moving according to the rules of chess, must visit each square exactly once. 

Following is an example path followed by Knight to cover all the cells. The below grid represents a chessboard with 8 x 8 cells. Numbers in cells indicate move number of Knight.   

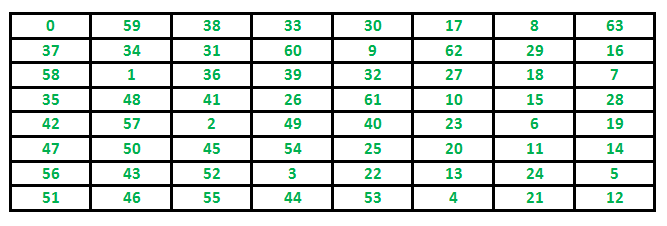
We have discussed Backtracking Algorithm for solution of Knight’s tour . In this post Warnsdorff’s heuristic is discussed.  Warnsdorff’s Rule:  

• We can start from any initial position of the knight on the board.
• We always move to an adjacent, unvisited square with minimal degree (minimum number of unvisited adjacent).

This algorithm may also more generally be applied to any graph. 

Some definitions:   

• A position Q is accessible from a position P if P can move to Q by a single Knight’s move, and Q has not yet been visited.
• The accessibility of a position P is the number of positions accessible from P.

Algorithm:   

• Set P to be a random initial position on the board
• Mark the board at P with the move number “1”
• let S be the set of positions accessible from P.
• Set P to be the position in S with minimum accessibility
• Mark the board at P with the current move number
• Return the marked board — each square will be marked with the move number on which it is visited.

Below is implementation of above algorithm.  

Output:  

Time complexity: O(N^3) Space complexity: O(N^2)

The Hamiltonian path problem is NP-hard in general. In practice, Warnsdorff’s heuristic successfully finds a solution in linear time.

Do you know?   “On an 8 × 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately, as are rotations and reflections). The number of undirected closed tours is half this number, since every tour can be traced in reverse!”

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to [email protected]. See your article appearing on the GeeksforGeeks main page and help other Geeks.  

Please Login to comment...

Similar reads.

• chessboard-problems
• Backtracking
• 10 Best Slack Integrations to Enhance Your Team's Productivity
• 10 Best Zendesk Alternatives and Competitors
• 10 Best Trello Power-Ups for Maximizing Project Management
• Google Rolls Out Gemini In Android Studio For Coding Assistance
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?