eulerian tour

Forgot password? New user? Sign up

Existing user? Log in

Eulerian Path

Already have an account? Log in here.

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once, and the study of these paths came up in their relation to problems studied by Euler in the 18th century like the one below:

Is there a walking path that stays inside the picture and crosses each of the bridges exactly once?

After trying and failing to draw such a path, it might seem plausible that the task is impossible. But how can this be proven? What if the configuration of bridges is slightly different? (For instance, it is not hard to cross all but one of the bridges, and adding another bridge to the existing seven would also allow a complete crossing.) Is there a way to characterize the configurations that allow for these paths? What if the path is required to start and end at the same place?

The answers to these questions were first supplied in 1736, by Leonhard Euler , in a paper that proved the first result in what is now known as graph theory . Paths traversing all the bridges (or, in more generality, paths traversing all the edges of the underlying graph) are known as Eulerian paths , and Eulerian paths which start and end at the same place are called Eulerian circuits .

The problem above is known as the Bridges of Konigsberg problem, named after a city in Prussia on the Pregel River with bridges configured as in the picture.

An informal proof

Graphs, eulerian paths, and eulerian circuits, fleury's algorithm, proof of the theorem, bridges of konigsberg revisited, five-room puzzle.

There are four landmasses in the picture. Every path that crosses the bridges will go back and forth between these four landmasses. Suppose there is a person standing on each landmass and watching someone walking the path, counting every time the walker either enters or exits the landmass (including the beginning and end of the path in their count). If there is a path that crosses each bridge exactly once, what will the counters' numbers be when the walker finishes?

The counter on the top will have \( 3 \), since each of the three bridges that hits his landmass will have been crossed exactly once, and each crossing will be counted as either an entry or an exit. Similarly, the counter on the middle island will show \( 5 \), the counter on the right will show \( 3\), and the counter at the bottom will show \( 3 \).

But the walker enters and exits each landmass every time he passes through, which contributes \( 2 \) to the count, so each counter's final count should be an even number--except for the two counters who count the beginning and the end of the path (the first exit doesn't have a corresponding entry, and the last entry doesn't have a corresponding exit). Still, it's impossible for all four counters to end with odd numbers, so there is no such path.

This problem can be rephrased in terms of graph theory , as follows. Consider the graph with vertices corresponding to the four landmasses, and edges between the vertices corresponding to the bridges. The path in question is a traversal of the graph that passes through each edge exactly once. Or, in other words, it is a drawing of the graph on a piece of paper without picking up our pencil or drawing any edge more than once.

In what follows, graphs will be assumed to be finite (with finitely many vertices and edges). Recall that the degree of a vertex in a graph is the number of edges that touch the vertex.

Here is the graph that corresponds to the bridge problem.

The degree of a vertex corresponding to one of the four landmasses in the original problem is the number that each counter will have in the above proof: the top, right, and bottom vertices have degree \( 3 \) and the left vertex has degree \( 5 \).

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once. It is an Eulerian circuit if it starts and ends at the same vertex. \(_\square\)

The informal proof in the previous section, translated into the language of graph theory, shows immediately that:

If a graph admits an Eulerian path, then there are either \( 0 \) or \( 2 \) vertices with odd degree. If a graph admits an Eulerian circuit, then there are \( 0 \) vertices with odd degree.

The more interesting and difficult statement is the converse. What conditions guarantee the existence of an Eulerian path or Eulerian circuit? It turns out that aside from the necessary conditions on degrees, the only other requirement is the obvious one that any two vertices of degree \(\ge 1\) have a path between them.

A graph is connected if there is a path between any two vertices. \(_\square\)

Every (finite) graph can be uniquely decomposed into connected components : each component is a connected subgraph, and there are no edges between any two components. A vertex of degree zero is its own connected component.

A graph has an Eulerian path if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) there are 0 or 2 vertices of odd degree. A graph has an Eulerian circuit if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) every vertex has even degree. \(_\square\)

Euler stated this theorem without proof when he solved the Bridges of Konigsberg problem in 1736, but the proof was not given until the late \(19^\text{th}\) century.

Can we color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once?

Define the cube graph \( C_n \) as follows:

There are \( 2^n \) vertices, labelled \( v_0, v_1, \ldots, v_{2^n-1} \). Draw an edge between \( v_a \) and \( v_b\) if and only if the binary representations of \( a \) and \( b\) differ in exactly one digit.

We would like to find a path along the cube graph \( C_n \) that crosses each edge exactly once, and begins and ends at the same vertex. For \( C_2 \) this is possible: start at 0, move to 2, move to 3, move to 1, move back to 0.

What about for \( n = 3 \) or \( n = 4 ? \)

To prove the theorem, the "only if" statements have been established by the above discussion. One way to prove the "if" statements is via the following algorithm due to Fleury which constructs an Eulerian path or circuit.

If there are two vertices of odd degree, start with one of them. Otherwise, start with any vertex. At every step of the algorithm, pick an edge that will not disconnect the graph if it is removed, unless there is no such edge. (Edges that will disconnect the graph if they are removed are--somewhat confusingly in this context--called bridges .) Move along this edge and delete it from the graph once done. Continue.

Every graph has an even number of vertices with odd degree.

Proof: Every edge hits two vertices, so the sum of the degrees of the vertices equals twice the number of edges. So it is even. The lemma follows immediately.

Rather than giving the details of this proof, here is an alternative algorithm due to Hierholzer that also works. The algorithm produces Eulerian circuits, but it can be modified to produce Eulerian paths if there are two vertices of odd degree.

Suppose every vertex has even degree. Start with a vertex \( v \) and follow a path around the graph until it returns to \( v\). This will always be possible because there will always be an odd number of unused edges emanating from a vertex that the path has landed on. This produces a circuit that may not be Eulerian; but if it is not, we can start from a vertex \(w\) with some unused edges coming from it and follow a path of unused edges around the graph until it returns to \( w \). The old circuit plus the new one can be traversed as one large circuit (start at \( v\), go to \( w\), do the \( w\) circuit, continue the rest of the \( v\) circuit). Repeat until there are no more unused edges. \( \square\)

A graph in which all vertices have even degree. [1] Consider the above graph. Starting at vertex 1, draw a circuit 1-2-3-7-1. There are unused edges emanating from vertex 1, so draw another circuit 1-3-4-7-8-1. Put them together to get 1-2-3-7-1-3-4-7-8-1. Now vertex 1 no longer has unused edges, but vertex 4 does: draw 4-5-9-4. Stick this into the previous circuit to get \[ 1-2-3-7-1-3-{\bf 4-5-9-4}-7-8-1. \] Finally, vertex 9 has some unused edges left, so draw the circuit 9-6-7-9 and notice that all the edges have been used. Stick it into the previous circuit to get \[ 1-2-3-7-1-3-4-5-{\bf 9-6-7-9}-4-7-8-1. \]

The Konigsberg bridges have the interesting property that adding or deleting a bridge between any two landmasses will allow an Eulerian path. Indeed, adding or deleting a bridge will change the parity of the degrees of two of the four vertices of the associated graph, which will make them both even. Then there will be two vertices of odd degree, which will imply the existence of an Eulerian path.

This illustrates the power of the theorem; without having to draw the paths in all of the various cases that might arise, nevertheless an affirmative answer can be given to the question of the existence of Eulerian paths.

Another application of the theorem is to the following puzzle:

Suppose five rooms in a house are laid out as follows: Imagine a door cut into each wall of each room (including the outside). Is there a path that goes through each door exactly once? The answer is no, as the associated graph has four vertices of odd degree. Here are the graphs for the Konigsberg and five-room problems, respectively, with degrees pictured on each vertex. Note that it is possible in the five-room problem to construct a path that passes through all but one door, but in this case only certain doors can be omitted; the door has to correspond to an edge connecting two odd-degree vertices. \(_\square\)

• Tin Tin, C. Hierholzer's algorithm . Retrieved August 8, 2008, from https://commons.wikimedia.org/wiki/File:Hierholzer_(3).png

Problem Loading...

Note Loading...

Set Loading...

Discrete Mathematics An Open Introduction

Oscar Levin

Section 4.4 Euler Paths and Circuits

Investigate 35.

An Euler path , in a graph or multigraph, is a walk through the graph which uses every edge exactly once. An Euler circuit is an Euler path which starts and stops at the same vertex. Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or circuit.

Which of the graphs below have Euler paths? Which have Euler circuits?

List the degrees of each vertex of the graphs above. Is there a connection between degrees and the existence of Euler paths and circuits?

Is it possible for a graph with a degree 1 vertex to have an Euler circuit? If so, draw one. If not, explain why not. What about an Euler path?

What if every vertex of the graph has degree 2. Is there an Euler path? An Euler circuit? Draw some graphs.

Below is part of a graph. Even though you can only see some of the vertices, can you deduce whether the graph will have an Euler path or circuit?

If we start at a vertex and trace along edges to get to other vertices, we create a walk through the graph. More precisely, a walk in a graph is a sequence of vertices such that every vertex in the sequence is adjacent to the vertices before and after it in the sequence. If the walk travels along every edge exactly once, then the walk is called an Euler path (or Euler walk ). If, in addition, the starting and ending vertices are the same (so you trace along every edge exactly once and end up where you started), then the walk is called an Euler circuit (or Euler tour ). Of course if a graph is not connected, there is no hope of finding such a path or circuit. For the rest of this section, assume all the graphs discussed are connected.

The bridges of Königsberg problem is really a question about the existence of Euler paths. There will be a route that crosses every bridge exactly once if and only if the graph below has an Euler path:

This graph is small enough that we could actually check every possible walk that does not reuse edges, and in doing so convince ourselves that there is no Euler path (let alone an Euler circuit). On small graphs which do have an Euler path, it is usually not difficult to find one. Our goal is to find a quick way to check whether a graph has an Euler path or circuit, even if the graph is quite large.

One way to guarantee that a graph does not have an Euler circuit is to include a “spike,” a vertex of degree 1.

The vertex \(a\) has degree 1, and if you try to make an Euler circuit, you see that you will get stuck at the vertex. It is a dead end. That is, unless you start there. But then there is no way to return, so there is no hope of finding an Euler circuit. There is however an Euler path. It starts at the vertex \(a\text{,}\) then loops around the triangle. You will end at the vertex of degree 3.

You run into a similar problem whenever you have a vertex of any odd degree. If you start at such a vertex, you will not be able to end there (after traversing every edge exactly once). After using one edge to leave the starting vertex, you will be left with an even number of edges emanating from the vertex. Half of these could be used for returning to the vertex, the other half for leaving. So you return, then leave. Return, then leave. The only way to use up all the edges is to use the last one by leaving the vertex. On the other hand, if you have a vertex with odd degree that you do not start a path at, then you will eventually get stuck at that vertex. The path will use pairs of edges incident to the vertex to arrive and leave again. Eventually all but one of these edges will be used up, leaving only an edge to arrive by, and none to leave again.

What all this says is that if a graph has an Euler path and two vertices with odd degree, then the Euler path must start at one of the odd degree vertices and end at the other. In such a situation, every other vertex must have an even degree since we need an equal number of edges to get to those vertices as to leave them. How could we have an Euler circuit? The graph could not have any odd degree vertex as an Euler path would have to start there or end there, but not both. Thus for a graph to have an Euler circuit, all vertices must have even degree.

The converse is also true: if all the vertices of a graph have even degree, then the graph has an Euler circuit, and if there are exactly two vertices with odd degree, the graph has an Euler path. To prove this is a little tricky, but the basic idea is that you will never get stuck because there is an “outbound” edge for every “inbound” edge at every vertex. If you try to make an Euler path and miss some edges, you will always be able to “splice in” a circuit using the edges you previously missed.

Euler Paths and Circuits

A graph has an Euler circuit if and only if the degree of every vertex is even.

A graph has an Euler path if and only if there are at most two vertices with odd degree.

Since the bridges of Königsberg graph has all four vertices with odd degree, there is no Euler path through the graph. Thus there is no way for the townspeople to cross every bridge exactly once.

Subsection Hamilton Paths

Suppose you wanted to tour Königsberg in such a way where you visit each land mass (the two islands and both banks) exactly once. This can be done. In graph theory terms, we are asking whether there is a path which visits every vertex exactly once. Such a path is called a Hamilton path (or Hamiltonian path ). We could also consider Hamilton cycles , which are Hamliton paths which start and stop at the same vertex.

Example 4.4.1

Determine whether the graphs below have a Hamilton path.

The graph on the left has a Hamilton path (many different ones, actually), as shown here:

The graph on the right does not have a Hamilton path. You would need to visit each of the “outside” vertices, but as soon as you visit one, you get stuck. Note that this graph does not have an Euler path, although there are graphs with Euler paths but no Hamilton paths.

It appears that finding Hamilton paths would be easier because graphs often have more edges than vertices, so there are fewer requirements to be met. However, nobody knows whether this is true. There is no known simple test for whether a graph has a Hamilton path. For small graphs this is not a problem, but as the size of the graph grows, it gets harder and harder to check wither there is a Hamilton path. In fact, this is an example of a question which as far as we know is too difficult for computers to solve; it is an example of a problem which is NP-complete.

Subsection Exercises

You and your friends want to tour the southwest by car. You will visit the nine states below, with the following rather odd rule: you must cross each border between neighboring states exactly once (so, for example, you must cross the Colorado-Utah border exactly once). Can you do it? If so, does it matter where you start your road trip? What fact about graph theory solves this problem?

This is a question about finding Euler paths. Draw a graph with a vertex in each state, and connect vertices if their states share a border. Exactly two vertices will have odd degree: the vertices for Nevada and Utah. Thus you must start your road trip at in one of those states and end it in the other.

Which of the following graphs contain an Euler path? Which contain an Euler circuit?

• \(K_5\text{.}\)
• \(K_{5,7}\)
• \(K_{2,7}\)
• \(K_4\) does not have an Euler path or circuit.
• \(K_5\) has an Euler circuit (so also an Euler path).
• \(K_{5,7}\) does not have an Euler path or circuit.
• \(K_{2,7}\) has an Euler path but not an Euler circuit.
• \(C_7\) has an Euler circuit (it is a circuit graph!)
• \(P_7\) has an Euler path but no Euler circuit.

Edward A. Mouse has just finished his brand new house. The floor plan is shown below:

Edward wants to give a tour of his new pad to a lady-mouse-friend. Is it possible for them to walk through every doorway exactly once? If so, in which rooms must they begin and end the tour? Explain.

Is it possible to tour the house visiting each room exactly once (not necessarily using every doorway)? Explain.

After a few mouse-years, Edward decides to remodel. He would like to add some new doors between the rooms he has. Of course, he cannot add any doors to the exterior of the house. Is it possible for each room to have an odd number of doors? Explain.

For which \(n\) does the graph \(K_n\) contain an Euler circuit? Explain.

When \(n\) is odd, \(K_n\) contains an Euler circuit. This is because every vertex has degree \(n-1\text{,}\) so an odd \(n\) results in all degrees being even.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain an Euler path? An Euler circuit? Explain.

If both \(m\) and \(n\) are even, then \(K_{m,n}\) has an Euler circuit. When both are odd, there is no Euler path or circuit. If one is 2 and the other is odd, then there is an Euler path but not an Euler circuit.

For which \(n\) does \(K_n\) contain a Hamilton path? A Hamilton cycle? Explain.

All values of \(n\text{.}\) In particular, \(K_n\) contains \(C_n\) as a subgroup, which is a cycle that includes every vertex.

For which \(m\) and \(n\) does the graph \(K_{m,n}\) contain a Hamilton path? A Hamilton cycle? Explain.

As long as \(|m-n| \le 1\text{,}\) the graph \(K_{m,n}\) will have a Hamilton path. To have a Hamilton cycle, we must have \(m=n\text{.}\)

A bridge builder has come to Königsberg and would like to add bridges so that it is possible to travel over every bridge exactly once. How many bridges must be built?

If we build one bridge, we can have an Euler path. Two bridges must be built for an Euler circuit.

Below is a graph representing friendships between a group of students (each vertex is a student and each edge is a friendship). Is it possible for the students to sit around a round table in such a way that every student sits between two friends? What does this question have to do with paths?

We are looking for a Hamiltonian cycle, and this graph does have one:

Suppose a graph has a Hamilton path. What is the maximum number of vertices of degree one the graph can have? Explain why your answer is correct.

Find a graph which does not have a Hamilton path even though no vertex has degree one. Explain why your example works.

Consider the following graph:

• Find a Hamilton path. Can your path be extended to a Hamilton cycle?
• Is the graph bipartite? If so, how many vertices are in each “part”?
• Use your answer to part (b) to prove that the graph has no Hamilton cycle.
• Suppose you have a bipartite graph \(G\) in which one part has at least two more vertices than the other. Prove that \(G\) does not have a Hamilton path.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.4: Traversals- Eulerian and Hamiltonian Graphs

• Last updated
• Save as PDF
• Page ID 80537

• Al Doerr & Ken Levasseur
• University of Massachusetts Lowell

The subject of graph traversals has a long history. In fact, the solution by Leonhard Euler (Switzerland, 1707-83) of the Koenigsberg Bridge Problem is considered by many to represent the birth of graph theory.

Eulerian Graphs

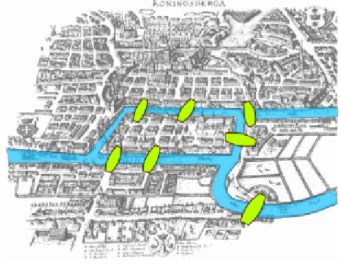
A map of the Prussian city of Koenigsberg (circa 1735) in Figure \(\PageIndex{1}\) shows that there were seven bridges connecting the four land masses that made up the city. The legend of this problem states that the citizens of Koenigsberg searched in vain for a walking tour that passed over each bridge exactly once. No one could design such a tour and the search was abruptly abandoned with the publication of Euler's Theorem.

Theorem \(\PageIndex{1}\): Euler's Theorem: Koenigsberg Case

No walking tour of Koenigsberg can be designed so that each bridge is used exactly once.

The map of Koenigsberg can be represented as an undirected multigraph, as in Figure \(\PageIndex{2}\). The four land masses are the vertices and each edge represents a bridge.

The desired tour is then a path that uses each edge once and only once. Since the path can start and end at two different vertices, there are two remaining vertices that must be intermediate vertices in the path. If \(x\) is an intermediate vertex, then every time that you visit \(x\text{,}\) you must use two of its incident edges, one to enter and one to exit. Therefore, there must be an even number of edges connecting \(x\) to the other vertices. Since every vertex in the Koenigsberg graph has an odd number of edges, no tour of the type that is desired is possible.

As is typical of most mathematicians, Euler wasn't satisfied with solving only the Koenigsberg problem. His original theorem, which is paraphrased below, concerned the existence of paths and circuits like those sought in Koenigsberg. These paths and circuits have become associated with Euler's name.

Definition \(\PageIndex{1}\): Eulerian Paths, Circuits, Graphs

An Eulerian path through a graph is a path whose edge list contains each edge of the graph exactly once. If the path is a circuit, then it is called an Eulerian circuit. An Eulerian graph is a graph that possesses an Eulerian circuit.

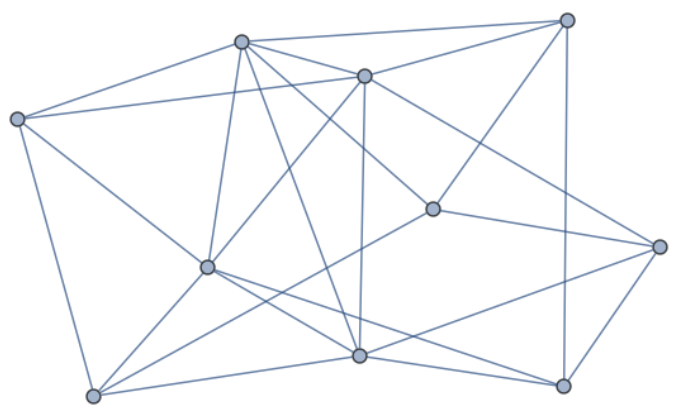
Example \(\PageIndex{1}\): An Eulerian Graph

Without tracing any paths, we can be sure that the graph below has an Eulerian circuit because all vertices have an even degree. This follows from the following theorem.

Theorem \(\PageIndex{2}\): Euler's Theorem: General Case

An undirected graph has an Eulerian path if and only if it is connected and has either zero or two vertices with an odd degree. If no vertex has an odd degree, then the graph is Eulerian.

It can be proven by induction that the number of vertices in an undirected graph that have an odd degree must be even. We will leave the proof of this fact to the reader as an exercise. The necessity of having either zero or two vertices of odd degree is clear from the proof of the Koenigsberg case of this theorem. Therefore, we will concentrate on proving that this condition is sufficient to ensure that a graph has an Eulerian path. Let \(k\) be the number of vertices with odd degree.

Phase 1. If \(k = 0\text{,}\) start at any vertex, \(v_0\text{,}\) and travel along any path, not using any edge twice. Since each vertex has an even degree, this path can always be continued past each vertex that you reach except \(v_0\text{.}\) The result is a circuit that includes \(v_0\text{.}\) If \(k =2\text{,}\) let \(v_0\) be either one of the vertices of odd degree. Trace any path starting at \(v_0\) using up edges until you can go no further, as in the \(k = 0\) case. This time, the path that you obtain must end at the other vertex of odd degree that we will call \(v_1\text{.}\) At the end of Phase 1, we have an initial path that may or may not be Eulerian. If it is not Eulerian, Phase 2 can be repeated until all of the edges have been used. Since the number of unused edges is decreased in any use of Phase 2, an Eulerian path must be obtained in a finite number of steps.

Phase 2. As we enter this phase, we have constructed a path that uses a proper subset of the edges in our graph. We will refer to this path as the current path. Let \(V\) be the vertices of our graph, \(E\) the edges, and \(E_u\) the edges that have been used in the current path. Consider the graph \(G' = \left(V, E - E_u\right)\text{.}\) Note that every vertex in \(G'\) has an even degree. Select any edge, \(e\text{,}\) from \(G'.\) Let \(v_a\) and \(v_b\) be the vertices that \(e\) connects. Trace a new path starting at \(v_a\) whose first edge is \(e\text{.}\) We can be sure that at least one vertex of the new path is also in the current path since \((V, E)\) is connected. Starting at \(v_a\text{,}\) there exists a path in \((V, E)\) to any vertex in the current path. At some point along this path, which we can consider the start of the new path, we will have intersected the current path. Since the degree of each vertex in \(G'\) is even, any path that we start at \(v_a\) can be continued until it is a circuit. Now, we simply augment the current path with this circuit. As we travel along the current path, the first time that we intersect the new path, we travel along it (see Figure \(\PageIndex{4}\)). Once we complete the circuit that is the new path, we resume the traversal of the current path.

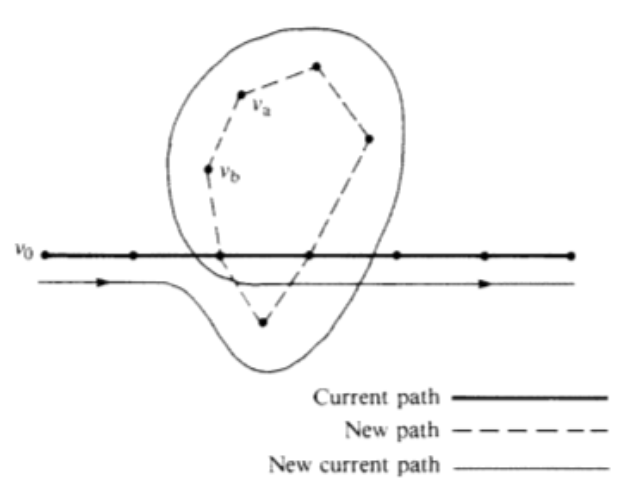
If the result of this phase is an Eulerian path, then we are finished; otherwise, repeat this phase.

Example \(\PageIndex{2}\): Complete Eulerian Graphs

The complete undirected graphs \(K_{2n+1}\text{,}\) \(n = 1, 2, 3, \ldots\text{.}\) .., are Eulerian. If \(n \geq 1\text{,}\) then \(K_{2n}\) is not Eulerian.

Hamiltonian Graphs

To search for a path that uses every vertex of a graph exactly once seems to be a natural next problem after you have considered Eulerian graphs.The Irish mathematician Sir William Rowan Hamilton (1805-65) is given credit for first defining such paths. He is also credited with discovering the quaternions, for which he was honored by the Irish government with a postage stamp in 2005.

Definition \(\PageIndex{2}\): Hamiltonian Path, Circuit, and Graphs

A Hamiltonian path through a graph is a path whose vertex list contains each vertex of the graph exactly once, except if the path is a circuit, in which case the initial vertex appears a second time as the terminal vertex. If the path is a circuit, then it is called a Hamiltonian circuit. A Hamiltonian graph is a graph that possesses a Hamiltonian circuit.

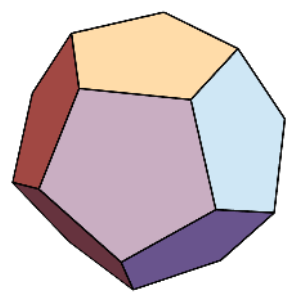
Example \(\PageIndex{3}\): The Original Hamiltonian Graph

Figure \(\PageIndex{7}\) shows a graph that is Hamiltonian. In fact, it is the graph that Hamilton used as an example to pose the question of existence of Hamiltonian paths in 1859. In its original form, the puzzle that was posed to readers was called “Around the World.” The vertices were labeled with names of major cities of the world and the object was to complete a tour of these cities. The graph is also referred to as the dodecahedron graph, where vertices correspond with the corners of a dodecahedron and the edges are the edges of the solid that connect the corners.

Problem \(\PageIndex{1}\)

Unfortunately, a simple condition doesn't exist that characterizes a Hamiltonian graph. An obvious necessary condition is that the graph be connected; however, there is a connected undirected graph with four vertices that is not Hamiltonian. Can you draw such a graph?

Note \(\PageIndex{1}\): What is Possible and What is Impossible?

The search for a Hamiltonian path in a graph is typical of many simple-sounding problems in graph theory that have proven to be very difficult to solve. Although there are simple algorithms for conducting the search, they are impractical for large problems because they take such a long time to complete as graph size increases. Currently, every algorithm to search for a Hamiltonian path in a graph takes a time that grows at a rate that is greater than any polynomial as a function of the number of vertices. Rates of this type are called “ super-polynomial .” That is, if \(T(n)\) is the time it takes to search a graph of \(n\) vertices, and \(p(n)\) is any polynomial, then \(T(n) > p(n)\) for all but possibly a finite number of positive values for \(n\text{.}\)

It is an unproven but widely held belief that no faster algorithm exists to search for Hamiltonian paths in general graphs. To sum up, the problem of determining whether a graph is Hamiltonian is theoretically possible; however, for large graphs we consider it a practical impossibility. Many of the problems we will discuss in the next section, particularly the Traveling Salesman Problem, are thought to be impossible in the same sense.

Definition \(\PageIndex{3}\): The \(n\)-cube

Let \(n \geq 1\text{,}\) and let \(B^n\) be the set of strings of 0's and 1's with length \(n\text{.}\) The \(n\)-cube is the undirected graph with a vertex for each string in \(B^n\) and an edge connecting each pair of strings that differ in exactly one position. The \(n\)-cube is normally denoted \(Q_n\text{.}\)

The \(n\)-cube is among the graphs that are defined within the graphs package of SageMath and is created with the expression graphs.CubeGraph(n) .

Example \(\PageIndex{4}\): Analog-to-Digital Conversion and the Gray Code

A common problem encountered in engineering is that of analog-to-digital (a-d) conversion, where the reading on a dial, for example, must be converted to a numerical value. In order for this conversion to be done reliably and quickly, one must solve an interesting problem in graph theory. Before this problem is posed, we will make the connection between a-d conversion and the graph problem using a simple example. Suppose a dial can be turned in any direction, and that the positions will be converted to one of the numbers zero through seven as depicted in Figure \(\PageIndex{8}\). The angles from 0 to 360 are divided into eight equal parts, and each part is assigned a number starting with 0 and increasing clockwise. If the dial points in any of these sectors the conversion is to the number of that sector. If the dial is on the boundary, then we will be satisfied with the conversion to either of the numbers in the bordering sectors. This conversion can be thought of as giving an approximate angle of the dial, for if the dial is in sector \(k\text{,}\) then the angle that the dial makes with east is approximately \({45k}^{\circ}\text{.}\)

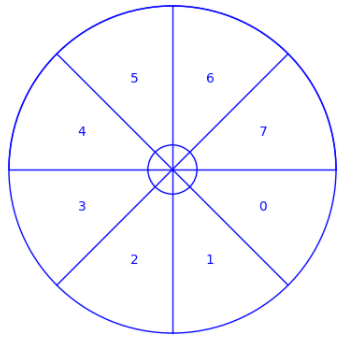
Now that the desired conversion has been identified, we will describe a “solution” that has one major error in it, and then identify how this problem can be rectified. All digital computers represent numbers in binary form, as a sequence of 0's and 1's called bits, short for binary digits. The binary representations of numbers 0 through 7 are:

\begin{equation*} \begin{array}{c} 0= {000}_{two} = 0 \cdot 4 + 0 \cdot 2 + 0 \cdot 1\\ 1= {001}_{two} = 0 \cdot 4 + 0 \cdot 2 + 1 \cdot 1\\ 2= {010}_{two} = 0 \cdot 4 + 1 \cdot 2 + 0 \cdot 1\\ 3= {011}_{two} = 0 \cdot 4 + 1 \cdot 2 + 1 \cdot 1\\ 4= {100}_{two} = 1 \cdot 4 + 0 \cdot 2 + 0 \cdot 1\\ 5= {101}_{two} = 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1\\ 6= {110}_{two} = 1 \cdot 4 + 1 \cdot 2 + 0 \cdot 1\\ 7= {111}_{two} = 1 \cdot 4 + 1 \cdot 2 + 1 \cdot 1\\ \end{array} \end{equation*}

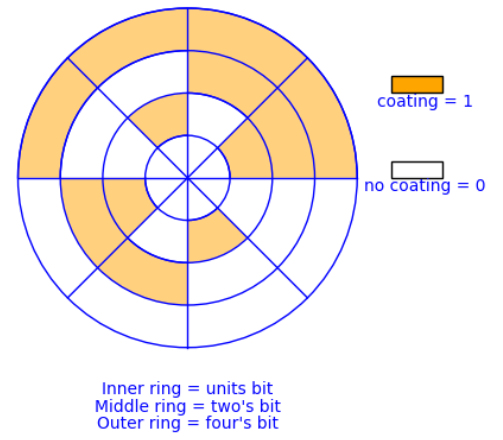
The way that we could send those bits to a computer is by coating parts of the back of the dial with a metallic substance, as in Figure \(\PageIndex{9}\). For each of the three concentric circles on the dial there is a small magnet. If a magnet lies under a part of the dial that has been coated with metal, then it will turn a switch ON, whereas the switch stays OFF when no metal is detected above a magnet. Notice how every ON/OFF combination of the three switches is possible given the way the back of the dial is coated.

If the dial is placed so that the magnets are in the middle of a sector, we expect this method to work well. There is a problem on certain boundaries, however. If the dial is turned so that the magnets are between sectors three and four, for example, then it is unclear what the result will be. This is due to the fact that each magnet will have only a fraction of the required metal above it to turn its switch ON. Due to expected irregularities in the coating of the dial, we can be safe in saying that for each switch either ON or OFF could be the result, and so if the dial is between sectors three and four, any number could be indicated. This problem does not occur between every sector. For example, between sectors 0 and 1, there is only one switch that cannot be predicted. No matter what the outcome is for the units switch in this case, the indicated sector must be either 0 or 1. This consistent with the original objective that a positioning of the dial on a boundary of two sectors should produce the number of either sector.

Is there a way to coat the sectors on the back of the dial so that each of the eight patterns corresponding to the numbers 0 to 7 appears once, and so that between any two adjacent sectors there is only one switch that will have a questionable setting? What we are describing here is a Hamiltonian circuit of the (Figure \(\PageIndex{10}\)). If one can draw a path along the edges in the 3-cube that starts at any vertex, passes through every other vertex once, and returns to the start, then that sequence of bit patterns can be used to coat the back of the dial so that between every sector there is only one questionable switch. Such a path is not difficult to find, as we will see below.

Many A-D conversion problems require many more sectors and switches than this example, and the same kinds of problems can occur. The solution would be to find a path within a much larger yet similar graph. For example, there might be 1,024 sectors with 10 switches, resulting in a graph with 1,024 vertices. Fortunately, our solution will apply to the \(n\)-cube for any positive value of \(n\text{.}\)

A Hamiltonian circuit of the \(n\)-cube can be described recursively. The circuit itself, called the Gray Code, is not the only Hamiltonian circuit of the \(n\)-cube, but it is the easiest to describe. The standard way to write the Gray Code is as a column of strings, where the last string is followed by the first string to complete the circuit.

Basis for the Gray Code (\(n = 1\)): The Gray Code for the 1-cube is \(G_1=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right)\text{.}\) Note that the edge between 0 and 1 is used twice in this circuit. That doesn't violate any rules for Hamiltonian circuits, but can only happen if a graph has two vertices.

Recursive definition of the Gray Code: Given the Gray Code for the \(n\)-cube, \(n \geq 1\text{,}\) then \(G_{n+1}\) is obtained by (1) listing \(G_n\) with each string prefixed with 0, and then (2) reversing the list of strings in \(G_n\) with each string prefixed with 1. Symbolically, the recursion can be expressed as follows, where \(G_n^r\) is the reverse of list \(G_n\text{.}\)

\begin{equation*} G_{n+1}=\left( \begin{array}{c} 0 G_n \\ 1 G_n^r \\ \end{array} \right) \end{equation*}

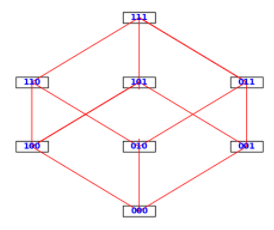
The Gray Codes for the 2-cube and 3-cube are

\begin{equation*} G_2= \left( \begin{array}{c} 00 \\ 01 \\ 11 \\ 10 \\ \end{array} \right) \textrm{ and }G_3=\left( \begin{array}{c} 000 \\ 001 \\ 011 \\ 010 \\ 110 \\ 111 \\ 101 \\ 100 \\ \end{array} \right) \end{equation*}

One question might come to mind at this point. If the coatings of the dial no longer in the sequence from 0 to 7, how would you interpret the patterns that are on the back of the dial as numbers from 0 to 7? In Chapter 14 we will see that if the Gray Code is used, this “decoding” is quite easy.

Example \(\PageIndex{5}\): Applications of the Gray Code

One application of the Gray code was discussed in the Introduction to this book. Another application is in statistics. In a statistical analysis, there is often a variable that depends on several factors, but exactly which factors are significant may not be obvious. For each subset of factors, there would be certain quantities to be calculated. One such quantity is the multiple correlation coefficient for a subset. If the correlation coefficient for a given subset, \(A\text{,}\) is known, then the value for any subset that is obtained by either deleting or adding an element to \(A\) can be obtained quickly. To calculate the correlation coefficient for each set, we simply travel along \(G_n\text{,}\) where \(n\) is the number of factors being studied. The first vertex will always be the string of 0's, which represents the empty set. For each vertex that you visit, the set that it corresponds to contains the \(k^{\text{th}}\) factor if the \(k^{\text{th}}\) character is a 1.

The 3-cube and its generalization, the \(n\)-cube, play a role in the design of a multiprocessor called a hypercube. A multiprocessor is a computer that consists of several independent processors that can operate simultaneously and are connected to one another by a network of connections. In a hypercube with \(M=2^n\) processors, the processors are numbered 0 to \(M-1\text{.}\) Two processors are connected if their binary representations differ in exactly one bit. The hypercube has proven to be the best possible network for certain problems requiring the use of a “supercomputer.”

Exercise \(\PageIndex{1}\)

Locate a map of New York City and draw a graph that represents its land masses, bridges and tunnels. Is there an Eulerian path through New York? You can do the same with any other city that has at least two land masses.

Using a recent road map, it appears that an Eulerian circuit exists in New York City, not including the small islands that belong to the city. Lowell, Massachusetts, is located at the confluence of the Merrimack and Concord rivers and has several canals flowing through it. No Eulerian path exists for Lowell.

Exercise \(\PageIndex{2}\)

Which of the drawings in Figure \(\PageIndex{11}\) can be drawn without removing your pencil from the paper and without drawing any line twice?

Exercise \(\PageIndex{3}\)

Write out the Gray Code for the 4-cube.

Gray Code for the 4-cube:

\begin{equation*} G_4=\left( \begin{array}{c} 0000 \\ 0001 \\ 0011 \\ 0010 \\ 0110 \\ 0111 \\ 0101 \\ 0100 \\ 1100 \\ 1101 \\ 1111 \\ 1110 \\ 1010 \\ 1011 \\ 1001 \\ 1000 \\ \end{array} \right) \end{equation*}

Exercise \(\PageIndex{4}\)

Find a Hamiltonian circuit for the dodecahedron graph in Figure \(\PageIndex{7}\).

Exercise \(\PageIndex{5}\)

The Euler Construction Company has been contracted to construct an extra bridge in Koenigsberg so that an Eulerian path through the town exists. Can this be done, and if so, where should the bridge be built?

Any bridge between two land masses will be sufficient. To get an Eulerian circuit, you must add a second bridge that connects the two land masses that were not connected by the first bridge.

Exercise \(\PageIndex{6}\)

Consider the graphs in Figure \(\PageIndex{12}\). Determine which of the graphs have an Eulerian path, and find an Eulerian path for the graphs that have one.

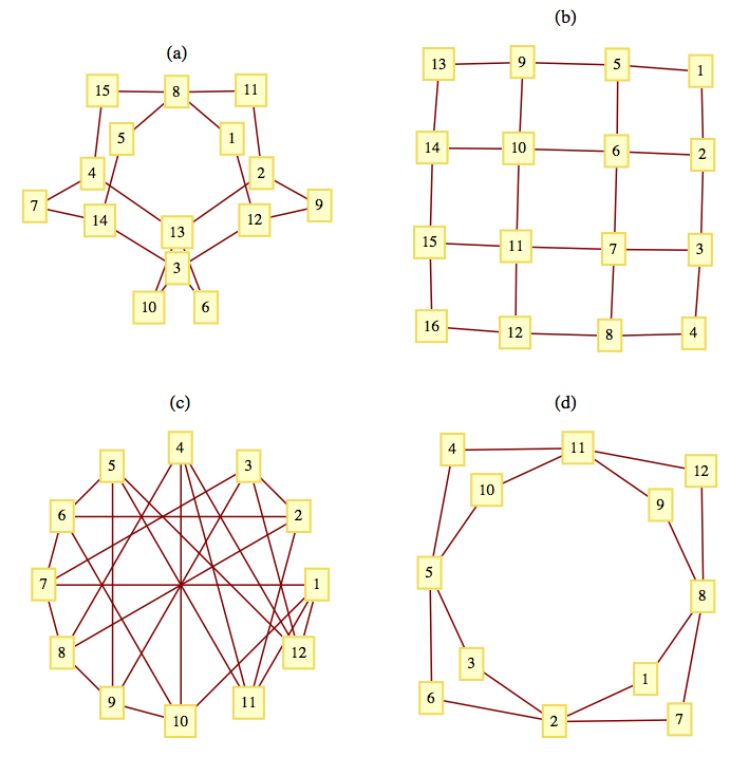
Exercise \(\PageIndex{7}\)

Formulate Euler's theorem for directed graphs.

Let \(G=(V,E)\) be a directed graph. \(G\) has an Eulerian circuit if and only if \(G\) is connected and \(indeg(v)= outdeg(v)\) for all \(v \in V\text{.}\) There exists an Eulerian path from \(v_1 \textrm{ to } v_2\) if and only if \(G\) is connected, \(indeg(v_1)=outdeg(v_1)-1\text{,}\) \(indeg(v_2)= outdeg(v_2)+1\text{,}\) and for all other vertices in \(V\) the indegree and outdegree are equal.

Exercise \(\PageIndex{8}\)

Prove that the number of vertices in an undirected graph with odd degree must be even.

Prove by induction on the number of edges.

Exercise \(\PageIndex{9}\)

• Under what conditions will a round-robin tournament graph be Eulerian?
• Prove that every round-robin tournament graph is Hamiltonian.

A round-robin tournament graph is rarely Eulerian. It will be Eulerian if it has an odd number of vertices and each vertex (team) wins exactly as many times as it loses. Every round-robin tournament graph has a Hamiltonian path. This can be proven by induction on the number of vertices.

Exercise \(\PageIndex{10}\)

For what values of \(n\) is the \(n\)-cube Eulerian?

Exercise \(\PageIndex{11}\)

A particular set of dominoes has 21 tiles: \((1, 1), (1, 2), \dots (1, 6), (2, 2), (2,3), \dots ,(6,6)\text{.}\) Is it possible to lay all 21 tiles in a line so that each adjacent pair of tile ends matches (that is, each 1 abuts a 1, and so on)?

No, such a line does not exist. The dominoes with two different numbers correspond with edges in a \(K_6\). See corresponding dominos and edges in Figure \(\PageIndex{13}\). Dominos with two equal numbers could be held back and inserted into the line created with the other dominoes if such a line exists. For example, if \((2,5),\: (5,4)\) were part of the line, \((5,5)\) could be inserted between those two dominoes. The line we want exists if and only if there exists an Eulerian path in a \(K_6\). Since all six vertices of a \(K_6\) have odd degree no such path exists.

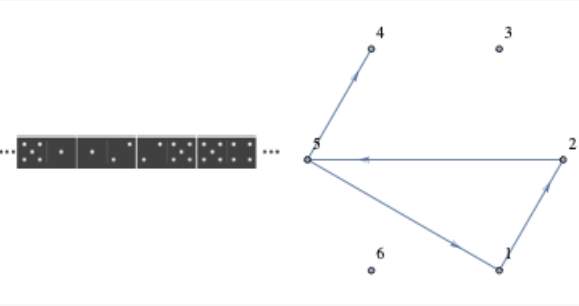
Figure \(\PageIndex{13}\): Correspondence between a line of dominos and a path in \(K_6\)

Eulerian Tour

Eulerian Cycle

FindEulerianCycle

FindEulerianCycle [ g ]

finds an Eulerian cycle in the graph g .

FindEulerianCycle [ g , k ]

finds at most k Eulerian cycles.

FindEulerianCycle [ { v  w , … } , … ]

uses rules v  w to specify the graph g .

• An Eulerian cycle is a cycle that traverses every edge exactly once.
• FindEulerianCycle returns a list of paths consisting of Eulerian cycles.
• FindEulerianCycle returns the list { } if no Eulerian cycles exist.
• FindEulerianCycle [ g ] is equivalent to FindEulerianCycle [ g , 1 ] .
• FindEulerianCycle [ g , All ] finds all Eulerian cycles in the graph g .
• FindEulerianCycle works with undirected graphs, directed graphs, and multigraphs.

Background & Context

• FindEulerianCycle attempts to find one or more distinct Eulerian cycles, also called Eulerian circuits, Eulerian tours, or Euler tours in a graph. The cycles are returned as a list of edge lists or as { } if none exist. An Eulerian cycle (more properly called a circuit when the cycle is identified using a explicit path with particular endpoints) is a consecutive sequence of distinct edges such that the first and last edge coincide at their endpoints and in which each edge appears exactly once. Eulerian cycles may be used to reconstruct genome sequences, construct de Bruijn sequences, and to find optimal conference scheduling.
• FindEulerianCycle [ g , k ] attempts to find k Eulerian cycles, where the count specification k may be omitted (in which case it is taken as 1), may be a positive integer, or may be All . Eulerian cycles need not be simple cycles, i.e. there can be a repeated vertex in a cycle (unlike Hamiltonian cycles, which are always simple).

• EulerianGraphQ can be used to determine if a graph is Eulerian. Functions for finding other sorts of cycles include FindCycle and FindHamiltonianCycle .

Basic Examples     (2)

Find an Eulerian cycle:

Show the cycle:

Find several Eulerian cycles:

Scope     (8)

FindEulerianCycle works with undirected graphs:

Directed graphs:

Multigraphs:

Find all Eulerian cycles:

Use rules to specify the graph:

FindEulerianCycle returns an empty result for non-Eulerian graphs:

FindEulerianCycle works with large graphs:

Applications     (7)

The seven bridges of the city of K ö nigsberg over the river Pregel cannot all be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began:

Trace out the figure of an envelope without lifting the pen and without going over the same line twice:

The graph is not Eulerian:

Since there are two odd-degree vertices, an augmented Eulerian graph is constructed by joining the odd-degree vertices via a new vertex (to avoid multiple edges):

Find an Eulerian cycle in the augmented graph:

Show the Eulerian path:

Find the most optimal scheduling of a conference room for the following meetings:

The graph of participants with edges connecting attendees of the same meeting:

There is no optimal schedule allowing two consecutive meetings to share a participant:

Add virtual meetings between participants with an odd number of meetings:

A possible scheduling:

Graph-based assembly of a circular genome "ATGGCGTGCA" with vertices as ( k -1 ) -mers and edges as k -mers:

Reconstruct the genome:

Construct a k -ary de Bruijn sequence from an Eulerian cycle:

De Bruijn sequence:

Find the order of vertices visited along a directed cycle:

Pick the source vertex of each edge:

Find an Eulerian cycle of the Dutch windmill graph:

Label the edges visited along the Eulerian cycle:

Properties & Relations     (6)

Use GraphData for an extensive collection of Eulerian graphs:

Non-Eulerian graphs:

Test whether a graph has an Eulerian cycle using EulerianGraphQ :

A connected undirected graph with vertices of even degree has an Eulerian cycle:

An undirected graph has an Eulerian cycle if it can be decomposed into edge-disjoint cycles:

The line graph of an undirected Eulerian graph has an Eulerian cycle:

A directed graph with in-degree and out-degree equal for each vertex has an Eulerian cycle:

Neat Examples     (1)

Dynamically highlight a cycle:

EulerianGraphQ   FindPostmanTour   FindHamiltonianCycle

Related Guides

• Paths, Cycles, and Flows

Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2015 (10.3)

Wolfram Research (2010), FindEulerianCycle, Wolfram Language function, https://reference.wolfram.com/language/ref/FindEulerianCycle.html (updated 2015).

Wolfram Language. 2010. "FindEulerianCycle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindEulerianCycle.html.

Wolfram Language. (2010). FindEulerianCycle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindEulerianCycle.html

@misc{reference.wolfram_2024_findeuleriancycle, author="Wolfram Research", title="{FindEulerianCycle}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindEulerianCycle.html}", note=[Accessed: 25-April-2024 ]}

@online{reference.wolfram_2024_findeuleriancycle, organization={Wolfram Research}, title={FindEulerianCycle}, year={2015}, url={https://reference.wolfram.com/language/ref/FindEulerianCycle.html}, note=[Accessed: 25-April-2024 ]}

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Search anything:

What is a Euler or Eulerian tour?

Graph algorithms euler tour eulerian tour.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Observations

• Discussions

Reading time: 10 minutes

An Euler tour or Eulerian tour in an undirected graph is a tour/ path that traverses each edge of the graph exactly once. Graphs that have an Euler tour are called Eulerian graphs.

Necessary and sufficient conditions

An undirected graph has a closed Euler tour if and only if it is connected and each vertex has an even degree.

An undirected graph has an open Euler tour (Euler path) if it is connected, and each vertex, except for exactly two vertices, has an even degree. The two vertices of odd degree have to be the endpoints of the tour.

A directed graph has a closed Euler tour if and only if it is strongly connected and the in-degree of each vertex is equal to its out-degree.

Similarly, a directed graph has an open Euler tour (Euler path) if and only if for each vertex the difference between its in-degree and out-degree is 0, except for two vertices, where one has difference +1 (the start of the tour) and the other has difference -1 (the end of the tour) and, if you add an edge from the end to the start, the graph is strongly connected.

If C is any cycle in a Eulerian graph, then after removing the edges of C, the remaining connected components will also be Eulerian graphs.

Use Depth First Search recursively to find eulerian path in a graph.

In an undirected eulerian graph, each vertex, except for exactly two vertices, has an even degree.

In a directed eulerian graph, the difference between its in-degree and out-degree is 0, except for two vertices, where one has difference +1 (the start of the tour) and the other has difference -1 (the end of the tour).

Adding an edge from end to start of a tour in a direct graph results in a strongly connected graph.

• 1 Definitions
• 2 Necessary and sufficient conditions
• 3 Fleury's algorithm
• 4.1 Pseudocode
• 5 Generalizations
• 6 Python implementation

Definitions [ edit ]

An Euler tour (or Eulerian tour) in an undirected graph is a tour that traverses each edge of the graph exactly once. Graphs that have an Euler tour are called Eulerian .

Some authors use the term "Euler tour" only for closed Euler tours.

Necessary and sufficient conditions [ edit ]

An undirected graph has a closed Euler tour iff it is connected and each vertex has an even degree.

An undirected graph has an open Euler tour (Euler path) if it is connected, and each vertex, except for exactly two vertices, has an even degree. The two vertices of odd degree have to be the endpoints of the tour.

A directed graph has a closed Euler tour iff it is strongly connected and the in-degree of each vertex is equal to its out-degree.

Similarly, a directed graph has an open Euler tour (Euler path) iff for each vertex the difference between its in-degree and out-degree is 0, except for two vertices, where one has difference +1 (the start of the tour) and the other has difference -1 (the end of the tour) and, if you add an edge from the end to the start, the graph is strongly connected.

Fleury's algorithm [ edit ]

Fleury's algorithm is a straightforward algorithm for finding Eulerian paths/tours. It proceeds by repeatedly removing edges from the graph in such way, that the graph remains Eulerian. A version of the algorithm, which finds Euler tour in undirected graphs follows.

Start with any vertex of non-zero degree. Choose any edge leaving this vertex, which is not a bridge (i.e. its removal will not disconnect the graph into two or more disjoint connected components). If there is no such edge, stop. Otherwise, append the edge to the Euler tour, remove it from the graph, and repeat the process starting with the other endpoint of this edge.

Though the algorithm is quite simple, it is not often used, because it needs to identify bridges in the graph (which is not a trivial thing to code.) Slightly more sophisticated, but easily implementable algorithm is presented below.

Cycle finding algorithm [ edit ]

This algorithm is based on the following observation: if C is any cycle in a Eulerian graph, then after removing the edges of C, the remaining connected components will also be Eulerian graphs.

The algorithm consists in finding a cycle in the graph, removing its edges and repeating this steps with each remaining connected component. It has a very compact code with recursion:

Pseudocode [ edit ]

This algorithm can also be used to find Eulerian paths: simply connect the path's endpoints by a dummy edge, and find Euler tour.

Generalizations [ edit ]

In some practical situations, it is desirable to find a cycle, which visits all edges of a graph, when the graph does not have an Euler tour. In this case some of the edges will have to be visited more than once. If the graph is weighted, and a minimum-cost such cycle is sought, then this is what is known as a Chinese Postman Problem .

It's possible to generalize Euler tours to the case of mixed graphs, which contain both directed and undirected edges. See article UVa_10735 for a description of one possible algorithm for such graphs.

Python implementation [ edit ]

This is a short implementation of the Euler tour in python.

• Graph Theory

Navigation menu

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Euler Tour of Tree

• Euler tour of Binary Tree
• Euler Tour | Subtree Sum using Segment Tree
• Number of ways to traverse an N-ary tree
• Combinatorics on ordered trees
• Possible number of Trees having N vertex
• Eulerian path and circuit for undirected graph
• Iterative Boundary Traversal of Complete Binary tree
• Sideways traversal of a Complete Binary Tree
• Conversion of an Undirected Graph to a Directed Euler Circuit
• Print leftmost and rightmost nodes of a Binary Tree
• Root to leaf paths having equal lengths in a Binary Tree
• Level order traversal of Binary Tree using Morris Traversal
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Sum of all the numbers that are formed from root to leaf paths
• Minimum distance to visit all the nodes of an undirected weighted tree
• Microsoft Full Time Interview (On Campus)
• Mathematics | Euler and Hamiltonian Paths
• Euler Graph and Arbitrarily Traceable Graphs in Graph Theory
• Crossword Puzzle Of The Week #18 (for Tree Data Structure)
• Merge Sort - Data Structure and Algorithms Tutorials
• Must Do Coding Questions for Companies like Amazon, Microsoft, Adobe, ...
• QuickSort - Data Structure and Algorithm Tutorials
• Bubble Sort - Data Structure and Algorithm Tutorials
• Tree Traversal Techniques - Data Structure and Algorithm Tutorials
• Binary Search - Data Structure and Algorithm Tutorials
• Insertion Sort - Data Structure and Algorithm Tutorials
• Selection Sort – Data Structure and Algorithm Tutorials
• Understanding the basics of Linked List
• Breadth First Search or BFS for a Graph

A Tree is a generalization of connected graph where it has N nodes that will have exactly N-1 edges, i.e one edge between every pair of vertices. Find the Euler tour of tree represented by adjacency list.

Input :   

Output : 1 2 3 2 4 2 1

Output : 1 5 4 2 4 3 4 5 1

Euler tour is defined as a way of traversing tree such that each vertex is added to the tour when we visit it (either moving down from parent vertex or returning from child vertex). We start from root and reach back to root after visiting all vertices. It requires exactly 2*N-1 vertices to store Euler tour.

Approach : We will run DFS(Depth first search) algorithm on Tree as:   

• Visit root node, i.e 1   vis[1]=1, Euler[0]=1  run dfs() for all unvisited adjacent nodes(2) 
• Visit node 2   vis[2]=1, Euler[1]=2  run dfs() for all unvisited adjacent nodes(3, 4) 
• Visit node 3   vis[3]=1, Euler[2]=3  All adjacent nodes are already visited, return to parent node  and add parent to Euler tour Euler[3]=2 
• Visit node 4   vis[4]=1, Euler[4]=4  All adjacent nodes are already visited, return to parent node  and add parent to Euler tour, Euler[5]=2 
• Visit node 2   All adjacent nodes are already visited, return to parent node  and add parent to Euler tour, Euler[6]=1 
• Visit node 1   All adjacent nodes are already visited, and node 1 is root node  so, we stop our recursion here. 

Similarly, for example 2:   

Implementation:

Complexity Analysis:

• Auxiliary Space: O(N) 
• Time Complexity: O(N)

Please Login to comment...

Similar reads.

Improve your Coding Skills with Practice

What kind of Experience do you want to share?