travel word problems

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

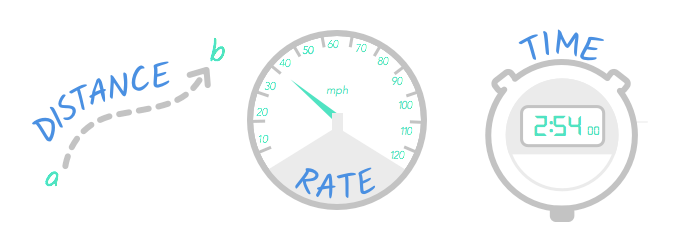
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

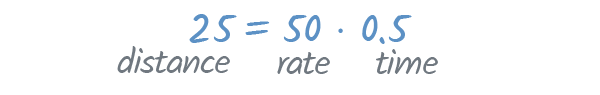
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

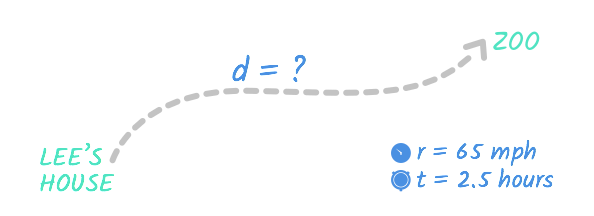
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

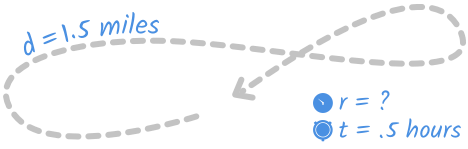
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

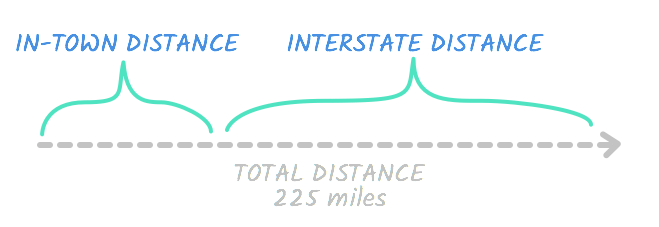
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

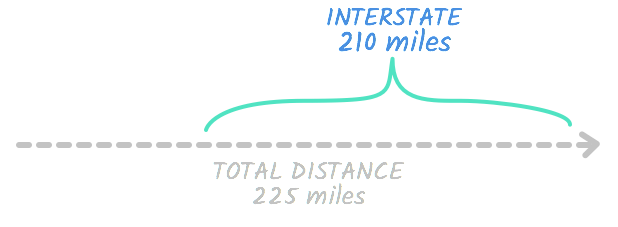
Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

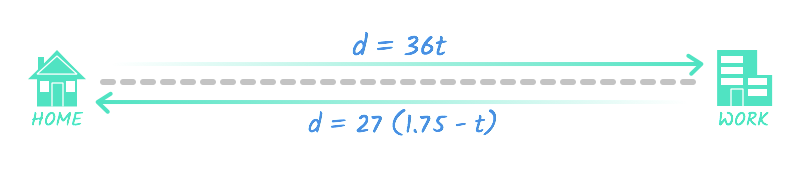
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

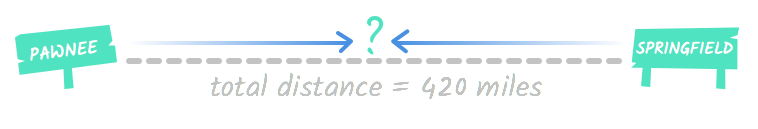
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

"Distance" Word Problems

Explanation More Examples

What is a "distance" word problem?

"Distance" word problems, often also called "uniform rate" problems, involve something travelling at some fixed and steady ("uniform") pace ("rate", "velocity", or "speed"), or else you are told to regard to object as moving at some average speed.

Content Continues Below

MathHelp.com

Distance Word Problems

Whenever you read a problem that involves "how fast", "how far", or "for how long", you should think of the distance equation, d = rt , where d stands for distance, r stands for the (constant or average) rate of speed, and t stands for time.

Make sure that the units for time and distance agree with the units for the rate. For instance, if they give you a rate of feet per second, then your time must be in seconds and your distance must be in feet. Sometimes they try to trick you by using mis-matched units, and you have to catch this and convert to the correct units.

In case you're wondering, this type of exercise requires that the rate be fixed and steady (that is, unchanging) for the d = rt formula to work. The only way you can deal with a speed that might be changing over time is to take the average speed over the time or distance in question. Working directly with changing speeds will be something you'll encounter in calculus, as it requires calculus-based (or more advanced) methods.

What is the difference between a fixed speed and an average speed?

A fixed-speed exercise is one in which the car, say, is always going exactly sixty miles an hour; in three hours, the car, on cruise-control, will have gone 180 miles. An average-speed exercise is one in which the car, say, averaged forty miles an hour, but this average includes the different speeds related to stop lights, highways, and back roads; in three hours the car went 120 miles, though the car's speed was not constant. Most of the exercises you'll see will be fixed-speed exercises, but obviously they're not very "real world". It's a simplification they do in order to make the situation feasible using only algebraic methods.

What is an example of a "distance" word problem?

• A 555 -mile, 5 -hour plane trip was flown at two speeds. For the first part of the trip, the average speed was 105 mph. Then the tailwind picked up, and the remainder of the trip was flown at an average speed of 115 mph. For how long did the plane fly at each speed?

There is a method for setting up and solving these exercises that I first encountered well after I'd actually been doing them while taking a class as an undergraduate. But, as soon as I was introduced to the method, I switched over, because it is *so* way easier.

First I set up a grid, with the columns being labelled with the variables from the "distance" formula, and the rows being labelled with the "parts" involved:

In the first part, the plane covered some distance. I don't know how much, so I'll need a variable to stand for this unknown value. I'll use the variable they give me in the distance equation:

They gave me the speed, or rate, for this part, so I'll add this to my table:

The plane flew for some amount of time during this first part, but I don't know how long that was. So I need a variable to stand for this unknown value; I'll use the variable from the distance equation:

For the second part, the plane travelled the rest of the total distance. I don't know the exact distance that was flown during this second part, but I do know that it was "however much was left of the 555 miles, after the first d miles were flown in the first part. "How much was left after [some amount] was taken out" is expressed with subtraction: I take the amount that has been taken care of already, and subtract this from whatever was the total. Adding this to my table, I get:

They've given me the speed, or rate, for the second part, and I can use the same "How much is left?" construction for whatever was the time for this second part. So now my table looks like this:

For the "total" row, I add down (or take info from the exercise statement):

Advertisement

Why did I not add down in the "rate" column? Because I cannot add rates! In this exercise, adding the rates would have said that the average rate for the entire trip was 105 + 115 = 220 miles per hour. But obviously this makes no sense.

The genius of this table-based method of set-up is that I can now create equations from the rows and columns. In this exercise, there is more than one way to proceed. I'll work with the "distance" equation to create expressions for the distances covered in each part.

Multiplying across, the first row tells me that the distance covered in the first part of the flight was:

1st part distance: 105 t

Again multiplying across, the second row tells me that the distance covered in the second part of the flight was:

2nd part distance: 115(5 − t )

I can add these two partial-distance expressions, and set them equal to the known total distance:

105 t + 115(5 − t ) = 555

This is an equation in one variable, which I can solve:

105 t + 115(5 − t ) = 555 105 t + 575 − 115 t = 555 575 − 10 t = 555 20 = 10 t 2 = t

Looking back at my table, I see the I had defined t to be the time that the plane spent in the air on the first part of its journey. Looking back at the original exercise, I see that they want to know the times that the plane spent at each of the two speeds.

I now have the time for the first part of the flight; the time was two hours. The exercise said that the entire trip was five hours, so the second part must have taken three hours (found by subtracting the first-part time from the total time). They haven't asked for the partial distances, so I now have all the information I need; no further computations are necessary. My answer is:

first part: 2 hours second part: 3 hours

When I was setting up my equation, I mentioned that there was more than one way to proceed. What was the other way? I could have used the table to create an expression for each of the two partial times, added, set the result equal to the given total, and solved for the variable d . Since the distance equation is d  =  rt , then the expressions for the partial times would be created by solving the equation for t  = . My work would have looked like this:

first part: d /105

second part: (555 − d )/115

adding: d /105 + (555 − d )/115 = 5 23 d + 11,655 − 21 d = 12,075 2 d = 420 d = 210

Looking back at my table, I would have seen that this gives me the distance covered in the first half of the flight. Looking back at the exercise, I would have seeing that they are wanting times, not distances. So I would have back-solved for the time for the first part, and then done the subtraction to find the time for the second part. My work would have had more steps, but my answer would have been the same.

There are three things that I hope you take from the above example:

• Using a table or grid to keep track of what you're doing can be incredibly helpful.
• It is important to clearly define your variables, so you know (by the end) what you'd meant (back in the beginning), so you can apply your results correctly.
• You should always check the original exercise, so you can be sure that you're answering the question that they'd actually asked.

(My value for the distance, found above, is correct, but was not what they'd asked for.) But even more important to understand is this:

NEVER TRY TO ADD RATES! Think about it: If you drive 20 mph on one street, and 40 mph on another street, does that mean you averaged 60 mph? Of course not.

Can I even average the rates? If I drove at 20 mph for one hour, and then drove 60 mph for two hours, then I would have travelled 140 miles in three hours, or a little under 47 mph. But 47 is not the average of 20 and 60 .

As you can see, the actual math involved in solving this type of exercise is often quite simple. It's the set-up that's the hard part. So what follows are some more examples, but with just the set-up displayed. Try your hand at solving, and click on the links to get pop-ups from which to check your equations and solutions.

• An executive drove from home at an average speed of 30 mph to an airport where a helicopter was waiting. The executive boarded the helicopter and flew to the corporate offices at an average speed of 60 mph. The entire distance was 150 miles; the entire trip took three hours. Find the distance from the airport to the corporate offices.

I will start in the usual way, by setting up my table:

I have labelled my rows so it's clear how they relate to the exercise. Now I need to fill in the rows. As before, I don't know the distance or the time for the part where the executive was driving, so I'll use variables for these unknowns, along with the given rate.

For the flying portion of the trip, I'll use the "how much is left" construction, along with the given rate, to fill in my second row. I'll also fill in the totals.

The first row gives me the equation d  = 30 t . The second row is messier, giving me the equation:

150 − d = 60(3 − t )

There are various ways I can go from here; I think I'll solve this second equation for the variable d , and then set the results equal to each other.

150 − d = 60(3 − t ) 150 − 60(3 − t ) = d

Setting equal these two expressions for d , I get:

30 t = 150 − 60(3 − t )

Solve for t ; interpret the value; state the final answer.

• A car and a bus set out at 2 p.m. from the same point, headed in the same direction. The average speed of the car is 30 mph slower than twice the speed of the bus. In two hours, the car is 20 miles ahead of the bus. Find the rate of the car.

Both vehicles travelled for the same amount of time.

The car's values are expressed in terms of the bus' values, so I'll use variables for the bus' unknowns, and then define the car in terms of the bus' variables. This gives me:

(As it turns out, I won't need the "total" row this time.) The car's row gives me:

d + 20 = 2(2 r − 30)

This is not terribly helpful. The second row gives me:

I'll use the second equation to simplify the first equation by substituting " 2 r " from the second equation in for the " d " in the first equation. Then I'll solve the equation for the value of " r ". Finally, I'll need to interpret this value within the context of the exercise, and then I'll state the final answer.

(Remember that the expression for the car's speed, from the table, was 2 r  − 30 , so all you need to do is find the numerical value of this expression. Just evaluate; don't try to solve — again — for the value of r .)

URL: https://www.purplemath.com/modules/distance.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Word Problems: Travel and Distance

Ask free tutors.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 3rd grade   >   Unit 12

• Time differences example
• Time differences (within 60 minutes)

Time word problem: travel time

• Time word problem: puzzle
• Telling time word problems (within the hour)

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Algebra: Distance Problems

In these lessons, we will learn to solve word problems involving distance, rate (speed) and time.

Related Pages Rate Distance Time Word Problems Distance Word Problems Average Speed Problems

What Are Distance Word Problems Or Distance Rate Time Problems?

Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time .

The formula for distance problems is: distance = rate × time or d = r × t

Things to watch out for: Make sure that you change the units when necessary. For example, if the rate is given in miles per hour and the time is given in minutes then change the units appropriately.

It would be helpful to use a table to organize the information for distance problems. A table helps you to think about one number at a time instead being confused by the question.

The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page for examples and solutions.

We will show you how to solve distance problems by the following examples:

• Traveling At Different Rates
• Traveling In Different Directions
• Given Total Time
• Wind and Current Problems

How To Solve Distance Problems: Traveling At Different Rates

Example: A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Solution: Step 1: Set up a rtd table.

Step 2: Fill in the table with information given in the question.

A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?

Let t = time to make the trip in Case 2.

Step 3: Fill in the values for d using the formula d = rt

Step 4: Since the distances traveled in both cases are the same, we get the equation:

Step 5: Beware - the question asked for “how many more minutes would it have taken to make the trip”, so we need to deduct the original 6 hours taken.

Answer: The time taken would have been 40 minutes longer.

How To Solve Distance Problems: Two Objects Traveling In The Same Direction

Example: This motion problem (or distance rate time problem or uniform rate problem) involves traveling in the same direction, solving for “how long” one moving object traveling until it meets up with the second moving object.

It uses d = rt (distance equals rate times time).

Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the same point A and heads for point B at 75 mph. How long before car 2 overtakes car 1?

How To Solve Distance Problems: Two Objects Traveling In The Opposite Directions

Example: A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

Let t = time when they are 210 miles apart.

Step 4: Since the total distance is 210, we get the equation:

50t + 55t = 210 105t = 210

Answer: They will be 210 miles apart in 2 hours.

Objects Traveling At Opposite Directions, Calculate How Long It Takes For Them To Be A Given Distance Apart

This motion problem (or distance rate time problem or uniform rate problem) involves one object traveling in one direction and the other in the opposite direction, solving for “how long” (or the amount of time) two moving objects traveling until they are certain distance apart.

Example: Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?

How To Solve Distance Problems: Given The Total Time

Example: John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?

John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?

Let t = time to travel to town.

7 – t = time to return from town.

40t = 30(7 – t) Use distributive property 40t = 210 – 30t

Step 5: The distance traveled by John to town is

40t = 120 The distance traveled by John to go back is also 120 So, the total distance traveled by John is 240

Answer: The distance traveled by John is 240 miles.

How To Find The Total Distance Given Total Time And Two Rates?

Example: Roy took 5 hours to complete a journey. For the first 2 hours, he traveled at an average speed of 65 km/h. For the rest of the journey, he traveled at an average speed of 78 km/h. What was the total distance of the journey?

How To Solve Wind And Current Word Problems?

There is another group of distance-time problems that involves the speed of the water current or the speed of wind affecting the speed of the vehicle. The following video shows an example of such a problem.

How to solve Wind Word Problems?

Example: Into the headwind, the plane flew 2000 miles in 5 hours. With a tailwind, the return trip took 4 hours. Find the speed of the plane in still air and the speed of the wind.

How to find the speed of the current of a stream?

Example: The speed of a boat in still water is 10 mph. It travels 24 miles upstream and 24 miles downstream in 5 hours. What is the speed of the current?

How to solve Current Word Problems?

Example: Traveling downstream, Elmo can go 6 km in 45 minutes. On the return trip, it takes him 1.5 hours. What is the boat’s speed in still water and what is the rate of the current?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Administrator
• Teacher How To's
• How It works
• All Worksheets
• Math Worksheets
• ELA Worksheets

Word Problems Activities

Teach your child all about word problems with amazing educational resources for children. These online word problems learning resources break down the topic into smaller parts for better conceptual understanding and grasp. Get started now to make word problems practice a smooth, easy and fun process for your child!

CONTENT TYPE

• Lesson Plans
• Math (8,010)
• Number Sense (1,465)
• Number Recognition (515)
• Number Recognition Within 3 (82)
• Number Recognition Within 5 (75)
• Number Recognition Within 10 (146)
• Number Recognition Within 20 (216)
• Number Sequence (86)
• Number Sequence Within 3 (6)
• Number Sequence Within 5 (15)
• Number Sequence Within 10 (28)
• Number Sequence Within 20 (15)
• Number Sequence Within 50 (5)
• Number Sequence Within 100 (5)
• Number Sequence Within 120 (4)
• Backward Sequence from 20 (10)
• Counting (330)
• Counting Objects Within 3 (13)
• Counting Objects Within 5 (54)
• Counting Objects Within 10 (86)
• Counting Objects Within 20 (13)
• Writing Numbers (470)
• Writing Numbers Within 3 (70)
• Writing Numbers Within 5 (65)
• Writing Numbers Within 10 (125)
• Writing Numbers Within 20 (210)
• Number Representation (82)
• Represent Numbers Using Place Value Blocks (10)
• Compare and Order Numbers (205)
• Compare Numbers (163)
• Compare Numbers within 10 (45)
• Compare Objects within 10 (16)
• Compare Without Visual Support (10)
• Compare Numbers within 20 (31)
• Compare Numbers Using Place Value Blocks (10)
• Compare Numbers Without Visual Support (10)
• Compare Numbers within 100 (46)
• Use Place Value Blocks to Compare Numbers (10)
• Compare Two 2-Digit Numbers (10)
• Compare 3-Digit Numbers (10)
• Compare Multi-Digit Numbers (10)
• Order Numbers (44)
• Order Numbers within 10 (3)
• Order Numbers within 20 (3)
• Order 3-Digit Numbers (10)
• Order Multi-Digit Numbers (11)
• Skip Counting (37)
• Skip Count by 2 (6)
• Skip Count by 5 (7)
• Skip Count by 10 (18)
• Skip Count by 100 (3)
• Even and Odd Numbers (28)
• Place Value (335)
• Read and Write Numbers (177)
• Numbers up to 10 (55)
• Numbers up to 20 (6)
• Numbers up to 50 (7)
• Numbers up to 100 (17)
• Identify Teen Numbers (12)
• Expanded Form (8)
• 3-Digit Numbers in Expanded Form (6)
• 4-Digit Numbers in Expanded Form (1)
• 5-Digit Numbers in Expanded Form (1)
• Standard Form (11)
• 3-Digit Numbers in Standard Form (6)
• 4-Digit Numbers in Standard Form (4)
• 5-Digit Numbers in Standard Form (1)
• Word Form (3)
• 3-Digit Numbers in Word Form (1)
• 4-Digit Numbers in Word Form (1)
• 5-Digit Numbers in Word Form (1)
• Unit Form (17)
• 3-Digit Numbers in Unit Form (5)
• 4-Digit Numbers in Unit Form (4)
• 5-Digit Numbers in Unit Form (3)
• Place Value Chart (17)
• 3-Digit Numbers on Place Value Chart (14)
• 4-Digit Numbers on Place Value Chart (1)
• 5-Digit Numbers on Place Value Chart (1)
• Round Numbers (47)
• Round Numbers to the Nearest 10 (18)
• Round Numbers to the Nearest 100 (14)
• Addition (1,331)
• Embedded Numbers (13)
• Addition Sentences (64)
• Addition Sentence within 5 (20)
• Addition Sentence within 10 (44)
• Add with Pictures (33)
• Add with Pictures within 5 (22)
• Add with Pictures within 10 (11)
• Model Addition (235)
• Addition Properties (16)
• Commutative Property of Addition (10)
• Add Using Models (18)
• Addition Strategies (500)
• Addition Strategies within 10 (287)
• Count All to Add (21)
• Count All to add within 5 (5)
• Count All to add within 10 (16)
• Count On to Add Strategy (40)
• Add using number line (10)
• Compose and Decompose Numbers (226)
• Number Bonds (197)
• Addition Strategies within 20 (130)
• Anchor 5 and 10 (21)
• Count On Strategy (24)
• Add with 10 (13)
• Make 10 Strategy (20)
• Doubles and Near Doubles Strategy to Add (38)
• Doubles Facts (13)
• Add Three Whole Numbers (18)
• Addition Strategies within 100 (54)
• Add using multiples of 10 (19)
• Addition Strategies within 1000 (36)
• Add using multiples of 100 (25)
• Addition Facts (208)
• Fluently Add within 5 (16)
• Fluently Add within 10 (83)
• Fluently Add within 20 (116)
• Equal Expressions (33)
• Addition Without Regrouping (238)
• Add within 100 without Regrouping (72)
• Add 2-digit number to 1-digit (17)
• Add 2-digit number to 2-digit (54)
• Add within 1000 without Regrouping (124)
• Add 10 to 3-digit numbers (15)
• Add 100 to 3-digit numbers (16)
• Add 3-digit number to 1-digit (16)
• Add 3-digit number to 2-digit (24)
• Add two 3-digit numbers (44)
• Add within 10000 without Regrouping (42)
• Addition With Regrouping (152)
• Add within 100 with Regrouping (51)
• Regroup and add 2-digit number to 1-digit (17)
• Regroup and add 2-digit numbers (17)
• Add within 1000 with Regrouping (57)
• Regroup ones and add (13)
• Regroup ones and tens and add (13)
• Regroup tens and add (3)
• Add within 10000 with Regrouping (44)
• Multi-digit Addition (108)
• Addition within 100000 (53)
• Addition within 1000000 (53)
• Subtraction (943)
• Subtraction Sentences (52)
• Subtraction Sentences within 5 (19)
• Subtraction Sentences within 10 (32)
• Subtract with Pictures (52)
• Subtract with Pictures within 5 (33)
• Subtract with Pictures within 10 (19)
• Model Subtraction (49)
• Subtract using Models (14)
• Subtraction Strategies (172)
• Subtraction Strategies within 10 (32)
• Count Back Strategy within 10 (25)
• Relate Addition and Subtraction within 10 (6)
• Subtraction Strategies within 20 (84)
• Count Back Strategy within 20 (44)
• Subtract using number line (10)
• Relate Addition and Subtraction within 20 (13)
• Doubles and Near Doubles Strategy to Subtract (4)
• Subtract from 10 Strategy (12)
• Subtraction Strategies within 100 (36)
• Subtract using multiples of 10 (20)
• Subtraction Strategies within 1000 (22)
• Subtract using multiples of 100 (11)
• Subtraction Facts (198)
• Fluently Subtract within 5 (17)
• Fluently Subtract within 10 (82)
• Fluently Subtract within 20 (110)
• Equal Expressions in Subtraction (28)
• Subtraction Without Regrouping (227)
• Subtract within 100 without Regrouping (83)
• Subtract Multiples of 10 (19)
• Subtract within 1000 without Regrouping (104)
• Subtract within 10000 without Regrouping (40)
• Subtraction With Regrouping (137)
• Subtract within 100 with Regrouping (49)
• Subtract within 1000 with Regrouping (52)
• Subtract across Zeros (5)
• Subtract within 10000 with Regrouping (36)
• Multi-digit Subtraction (110)
• Subtraction within 100000 (56)
• Subtraction within 1000000 (52)
• Multiplication (670)
• Arrays (23)
• Equal Groups (26)
• Multiplication Sentences (53)
• Repeated Addition to Multiply (18)
• Multiplication on Number Line (6)
• Multi-digit Multiplication (162)
• Multiply 2-digit by 1-digit Numbers (35)
• Multiply 2-digit by 2-digit numbers (55)
• Multiply 3-digit by 1-digit Numbers (18)
• Multiply 3-digit by 2-digit numbers (25)
• Multiply 4-digit by 1-digit Numbers (17)
• Multiplication Properties (105)
• Associative Property (12)
• Commutative Property (14)
• Distributive Property (61)
• Multiply by 0 and 1 (13)
• Estimate Products (12)
• Multiply by multiples of 10 (27)
• Times Tables (206)
• Multiplication Facts (193)
• Multiplication Facts of 2 (19)
• Multiplication Facts of 3 (19)
• Multiplication Facts of 4 (19)
• Multiplication Facts of 5 (19)
• Multiplication Facts of 6 (19)
• Multiplication Facts of 7 (18)
• Multiplication Facts of 8 (18)
• Multiplication Facts of 9 (19)
• Multiplication Facts of 10 (17)
• Multiply by 11 (15)
• Multiply by 12 (15)
• Division (383)
• Division Facts (138)
• Division Facts of 2 (15)
• Division Facts of 3 (17)
• Division Facts of 4 (17)
• Division Facts of 5 (15)
• Division Facts of 6 (18)
• Division Facts of 7 (15)
• Division Facts of 8 (16)
• Division Facts of 9 (15)
• Division Facts of 10 (14)
• Divide on a Number Line (13)
• Long Division (116)
• Divide 2-digit by 1-digit Numbers (21)
• Divide 3-digit by 1-digit Numbers (19)
• Divide 4-digit by 1-digit Numbers (15)
• Divide Multiples of 10 or 100 (20)
• Estimate Quotients (29)
• Fractions (609)
• Identify Fractions (54)
• Identify fractions using models (18)
• Identify fractions on the number line (17)
• Represent Fractions (44)
• Represent fractions on the number line (10)
• Mark fractions on the number line (10)
• Represent fractions using models (10)
• Represent fractions using real-word objects (10)
• Represent Mixed Numbers (10)
• Represent mixed numbers using models (10)
• Compare Fractions (65)
• Compare fractions using visual models (13)
• Compare fractions using number lines (14)
• Compare fractions without visual models (11)
• Benchmark Fractions (16)
• Order Fractions (20)
• Order fractions using visual models (10)
• Order fractions without visual models (10)
• Equivalent Fractions (52)
• Equivalent fractions using models (10)
• Equivalent fractions using number lines (10)
• Equivalent fractions without visual models (15)
• Identify equivalent fractions (10)
• Convert Fractions (35)
• Fractions as Mixed Numbers (10)
• Mixed Numbers as Fractions (25)
• Fractions Operations (324)
• Add and Subtract Fractions (110)
• Add Fractions (57)
• Represent Fraction Addition (9)
• Add fractions using models (12)
• Add like fractions (12)
• Add unlike fractions (10)
• Estimate fraction sums (13)
• Subtract Fractions (39)
• Represent Fraction Subtraction (9)
• Subtract fractions using models (9)
• Subtract like fractions (12)
• Subtract unlike fractions (10)
• Add and Subtract mixed numbers (81)
• Add mixed numbers (40)
• Add mixed numbers using models (10)
• Add a mixed number to a fraction (12)
• Add two mixed numbers (11)
• Subtract mixed numbers (41)
• Subtract mixed numbers using models (10)
• Subtract a fraction from a mixed number (14)
• Subtract two mixed numbers (10)
• Multiply Fractions (122)
• Multiply fractions by whole numbers (14)
• Multiply fractions by whole numbers without models (10)
• Multiply two fractions (20)
• Multiply fractions using models (10)
• Multiply fractions without models (10)
• Multiply mixed numbers (32)
• Multiply mixed numbers by whole numbers (10)
• Multiply mixed numbers by fractions (10)
• Multiply two mixed numbers (10)
• Fraction multiplication as scaling (10)
• Divide fractions (8)
• Decimals (1,729)
• Identify tenths (7)
• Identify hundredths (8)
• Represent Decimals (32)
• Represent Decimals Using Models (18)
• Represent Decimals on Number Lines (14)
• Read and Write Decimals (42)
• Decimals Expanded Form (20)
• Compose Decimals (10)
• Decompose Decimals (10)
• Decimals Standard Form (11)
• Decimals Word Form (10)
• Decimal Place Value (34)
• Digits at the given decimal place (10)
• Place values of digits in decimals (10)
• Compare and Order Decimals (76)
• Compare decimals (45)
• Compare decimals using models (20)
• Compare using decimal grids (10)
• Compare using decimal number lines (10)
• Compare decimals using place value (10)
• Order decimals (31)
• Order decimals using place value (10)
• Round Decimals (42)
• Round decimals to the nearest whole (12)
• Round decimals to the nearest tenths (10)
• Round decimals to the nearest hundredths (10)
• Convert Between Decimals and Fractions (7)
• Convert Decimals to Fractions (7)
• Equivalent Decimals (27)
• Tenths to hundredths (9)
• Hundredths to tenths (8)
• Decimal Operations (1,459)
• Add Decimals (699)
• Add tenths and hundredths (360)
• Add decimals without regrouping (194)
• Add decimals with regrouping (188)
• Subtract Decimals (705)
• Subtract decimals without regrouping (194)
• Subtract decimals with regrouping (184)
• Multiply Decimals (237)
• Multiply decimals by powers of 10 (83)
• Multiply decimals by whole numbers (128)
• Multiply decimals by decimals (72)
• Divide Decimals (161)
• Divide decimals by powers of 10 (20)
• Divide decimals by whole numbers (41)
• Divide whole numbers by decimals (45)
• Divide decimals by decimals (41)
• Types of Decimals (12)
• Geometry (292)
• Parallel lines (5)
• Angles (15)
• Positional Words (15)
• Sides and Corners (12)
• Corners (11)
• Shapes (200)
• 2d Shapes (162)
• Identify Quadrilaterals (24)
• Trapezoids (10)
• Identify triangles (14)
• Identify polygons (10)
• Attributes of 2D shapes (20)
• Sort 2D shapes (14)
• Partition 2D Shapes (28)
• Partition into equal parts (24)
• Halves, Thirds, and Fourths (18)
• 3d Shapes (20)
• Flat and Solid Shapes (23)
• Match 2D Shapes (9)
• Match 3D Shapes (10)
• 3D Shapes in real life (10)
• Coordinate Planes (28)
• Identify Points on the Coordinate Plane (10)
• Plot on the Coordinate Plane (11)
• Measurement (282)
• Capacity (22)
• Comparing Measurements (53)
• Compare Weights (13)
• Group of Objects (4)
• Compare Lengths (24)
• Compare Heights (14)
• Conversion of Measurement Units (16)
• Data Handling (73)
• Organize and Interpret Data (57)
• Organize data in bar graphs (7)
• Organize data in line plots (6)
• Organize data in picture graphs (4)
• Interpret data in bar graphs (5)
• Interpret data in line plots (7)
• Interpret data in picture graphs (6)
• Sort Objects (11)
• Length (39)
• Measure Lengths (19)
• Measure Lengths using the ruler (17)
• Estimate Lengths (4)
• Area of Shapes (18)
• Area of 2D Shapes (5)
• Area as Additive (5)
• Perimeter (19)
• Perimeter of Shapes (19)
• AM and PM (12)
• Analog Clock (32)
• Hour hand (12)
• Set time (10)
• Digital Clock (9)
• Elapsed Time (3)
• Time in Half Hours (19)
• Time in Hours (17)
• Time in Quarter Hours (19)
• Time to the Nearest 5 Minutes (21)
• Time to the Nearest Minute (2)
• Money (128)
• Identify Coins (20)
• Value of the Coins (10)
• Make Amounts (10)
• Counting Money (103)
• Compare Money (15)
• Count Money with Coins (37)
• Penny, Nickel, and Dime (20)
• Quarters and Half Dollar (9)
• Operations With Money (24)
• Add and Subtract Money (12)
• Multiply and Divide Money (7)
• Algebra (146)
• Patterns (35)
• Number Patterns (35)
• Extend Number Patterns (10)
• Generate Number Patterns (10)
• Relationship Between Patterns (10)
• Numerical Expressions (41)
• Interpret Numerical Expressions (10)
• Evaluate Numerical Expressions (21)
• Evaluate Exponents (10)
• Order of Operations (10)
• Factors and Multiples (51)
• Factors (30)
• Multiples (14)
• Prime and Composite Numbers (15)
• Word Problems (705)
• Addition and Subtraction Word Problems (396)
• Addition Word Problems (174)
• Addition Word Problems within 10 (29)
• Addition Word Problems within 20 (28)
• Addition Word Problems within 100 (44)
• Add to Compare Word Problems (21)
• Subtraction Word Problems (112)
• Subtraction Word Problems within 10 (17)
• Subtraction Word Problems within 20 (14)
• Subtraction Word Problems within 100 (28)
• Subtract to Compare Word Problems (16)
• Decimal Subtraction Word Problems (25)
• Multiplication and Division Word Problems (180)
• Multiplication Word Problems (104)
• Division Word Problems (73)
• Fraction Word Problems (34)
• Multi-step Word Problems (81)
• Money Word Problems (10)
• ELA (7,781)
• Reading (5,206)
• Phonics (4,916)
• Bossy R (27)
• Words with AR (10)
• Words with ER (8)
• Words With IR (8)
• Words with OR (7)
• Words with UR (8)
• Diphthongs (28)
• Words with OI (11)
• Words with OU (11)
• Words with OW (11)
• Words with OY (11)
• Ending Consonant Blends (91)
• CK Blend (7)
• LF Blend (13)
• LK Blend (14)
• LT Blend (13)
• MP Blend (12)
• ND Blend (13)
• NK Blend (14)
• SK Blend (12)
• ST Blend (12)
• NG Blend (7)
• Beginning Consonant Blends (101)
• L Blend Words (40)
• BL Blend (14)
• CL Blend (13)
• FL Blend (13)
• GL Blend (10)
• PL Blend (11)
• SL Blend (10)
• R Blend Words (36)
• CR Blend (12)
• FR Blend (12)
• GR Blend (11)
• PR Blend (13)
• TR Blend (12)
• SPL Blend (9)
• SQU Blend (8)
• STR Blend (8)
• Alphabet (581)
• Letter A (23)
• Letter B (27)
• Letter C (22)
• Letter D (28)
• Letter E (22)
• Letter F (23)
• Letter G (28)
• Letter H (24)
• Letter I (26)
• Letter J (26)
• Letter K (22)
• Letter L (22)
• Letter M (23)
• Letter N (25)
• Letter O (22)
• Letter P (29)
• Letter Q (27)
• Letter R (22)
• Letter S (22)
• Letter T (23)
• Letter U (22)
• Letter V (22)
• Letter W (22)
• Letter X (22)
• Letter Y (22)
• Letter Z (22)
• Letter Sequence (64)
• ABC Song (20)
• Alphabetical Order (34)
• Letter Sounds (468)
• Letter Sound A (21)
• Letter Sound B (21)
• Letter Sound C (21)
• Letter Sound D (22)
• Letter Sound E (20)
• Letter Sound F (21)
• Letter Sound G (22)
• Letter Sound H (22)
• Letter Sound I (19)
• Letter Sound J (19)
• Letter Sound K (21)
• Letter Sound L (20)
• Letter Sound M (21)
• Letter Sound N (17)
• Letter Sound O (20)
• Letter Sound P (21)
• Letter Sound Q (17)
• Letter Sound R (21)
• Letter Sound S (21)
• Letter Sound T (21)
• Letter Sound U (17)
• Letter Sound V (18)
• Letter Sound W (20)
• Letter Sound X (16)
• Letter Sound Y (19)
• Letter Sound Z (17)
• Beginning and Ending Sounds (25)
• Letter Recognition (365)
• Lowercase Letters (78)
• Uppercase Letters (78)
• Matching Lowercase and Uppercase Letters (209)
• Match Aa - Dd (9)
• Match Ee - Gg (7)
• Match Hh - Kk (9)
• Match Ll - Pp (11)
• Match Qq - Ss (7)
• Match Tt - Vv (7)
• Match Ww - Zz (9)
• Vowels (321)
• Long Vowel Sounds (128)
• Long A Vowel Sound (28)
• Long E Vowel Sound (27)
• Long I Vowel Sound (26)
• Long O Vowel Sound (24)
• Long U Vowel Sound (25)
• Magic - E (37)
• Magic E Words with Long Vowel A (12)
• Magic E Words with Long Vowel E (6)
• Magic E Words with Long Vowel I (12)
• Magic E Words with Long Vowel O (11)
• Magic E Words with Long Vowel U (11)
• Short Vowel Sounds (151)
• Short A Vowel Sound (77)
• Short E Vowel Sound (38)
• Short I Vowel Sound (77)
• Short O Vowel Sound (55)
• Short U Vowel Sound (35)
• Vowel Teams (49)
• Words with AI and AY (13)
• Words with EA and EE (14)
• Words with IE and Y (11)
• Words with OA and OW (13)
• Words with OO (11)
• Words with UE and UI (9)
• Blending (955)
• CCVC Words (64)
• CCVCC Words (36)
• CVC Words (453)
• CVCC Words (156)
• Beginning Blending (34)
• CCVC and CCVCC Words (28)
• CVCC and CCVCC Words (46)
• Words With Bossy R (45)
• Words With Diphthongs (18)
• Words With Three Letter Blends (14)
• Words With Trigraphs (28)
• Words With Vowel Teams (50)
• Consonant Digraphs (39)
• Digraph CH (17)
• Digraph CK (5)
• Digraph NG (5)
• Digraph PH (11)
• Digraph SH (18)
• Digraph TH (17)
• Digraph WH (17)
• Double Consonants (43)
• FF Words (13)
• LL Words (17)
• SS Words (15)
• ZZ Words (12)
• Rhyming Words (174)
• Trigraphs (29)
• Trigraph DGE (9)
• Trigraph IGH (7)
• Trigraph SHR (8)
• Trigraph TCH (7)
• Trigraph THR (7)
• Soft Sounds (2)
• Words with Soft C (1)
• Words with Soft G (1)
• Three Letter Blends (5)
• Sight Words (1,943)
• Dolch Sight Words (567)
• Fry Sight Words (444)
• Syllables (8)
• Hard and Soft Sounds of C and G (2)
• Segmenting Phonemes (1)
• Adding Deleting and Substituting Phonemes (6)
• Silent Letter Words (11)
• Reading Skills (276)
• Cause and Effect (21)
• Inference (19)
• Identify the Main Idea (40)
• Categorize Pictures into Groups (4)
• Choose a Suitable Heading (5)
• Prediction (14)
• Sequencing (28)
• Arrange Pictures in Order (3)
• Arrange Sentences in Order (4)
• Story Elements (20)
• Authors Purpose (9)
• Compare and Contrast (14)
• Ask and Answer Questions (6)
• Central Message (4)
• Point of View (12)
• Sensory Words (3)
• Comprehension (21)
• Character Analysis (16)
• Text Structure (9)
• Fact or Opinion (2)
• Reality and Fantasy (6)
• Using Illustrations (15)
• Using Text Features (8)
• Context Clues (13)
• Evaluating Authors Argument and Evidence (6)
• Communication Skills (14)
• Listening Skills (3)
• Speaking Skills (11)
• Writing (1,836)
• Handwriting (1,652)
• Letter Tracing (356)
• Letter Tracing A (33)
• Letter Tracing B (34)
• Letter Tracing C (33)
• Letter Tracing D (33)
• Letter Tracing E (33)
• Letter Tracing F (34)
• Letter Tracing G (33)
• Letter Tracing H (34)
• Letter Tracing I (33)
• Letter Tracing J (33)
• Letter Tracing K (33)
• Letter Tracing L (33)
• Letter Tracing M (34)
• Letter Tracing N (33)
• Letter Tracing O (33)
• Letter Tracing P (33)
• Letter Tracing Q (33)
• Letter Tracing R (33)
• Letter Tracing S (33)
• Letter Tracing T (33)
• Letter Tracing U (33)
• Letter Tracing V (33)
• Letter Tracing W (33)
• Letter Tracing X (33)
• Letter Tracing Y (33)
• Letter Tracing Z (33)
• Word Tracing (300)
• Cursive Writing (742)
• Writing Sight Words (60)
• Creative Writing (124)
• Grammar (392)
• Adverbs and Adjectives (71)
• Nouns and Pronouns (135)
• Pronouns (25)
• Parts of Speech (12)
• Prepositions and Conjunctions (36)
• Conjunctions (6)
• Prepositions (13)
• Punctuation (23)
• Sentences (27)
• Verbs and Tenses (100)
• Determiners (2)
• Article A An The (2)
• Spelling (29)
• Common Misspellings (10)
• Unscramble (16)
• Vocabulary (307)
• Abbreviations and Contractions (11)
• Affixes (17)
• Inflectional Endings (2)
• Commonly Confused Words (28)
• Compound Words (10)
• Figures of Speech (14)
• Similes and Metaphors (6)
• Alliteration (2)
• Synonyms and Antonyms (23)
• Word Puzzles (81)
• Shades of Meaning (4)
• Sorting Words into Categories (21)
• Making Connections in Reading (6)
• Flashcards (45)
• Vocabulary Flashcards (1)
• Phonics Flashcards (42)
• Grammar Flashcards (2)
• General Knowledge (295)
• Vegetables (19)
• Fruits (24)
• Dessert (9)
• Animals (58)
• Underwater (9)
• Dinosaurs (8)
• Reptiles (9)
• Seasonal (28)
• Christmas (12)
• Halloween (8)
• Kitchen (11)
• Utensils (6)
• Musical Instruments (30)
• Transport (9)
• Vehicles (9)
• Insects (9)
• Professions (8)
• Monuments (8)
• Household Items (8)
• Flowers (8)
• Buildings (8)
• Art & Creativity (236)
• Coloring (181)
• Animals (32)
• Underwater (8)
• Reptiles (8)
• Vegetables (8)
• Transport (8)
• Vehicles (8)
• Musical Instruments (8)
• Kitchen (8)
• Utensils (5)
• Insects (8)
• Rhymes (25)
• Cooking (7)
• Stories (10)
• Logic & Thinking (16)
• Puzzles (11)
• Matching (3)
• Multiplayer (12)
• Time Based (12)
• Player vs Player (12)
• Motor Skills (16)
• Fine Finger Movement (9)
• Aiming and Precision (6)

Addition and Subtraction Word Problems

Represent 'Add To' Scenarios Game

Learn to solve math problems through our 'Represent 'Add To' Scenarios' game.

Solve 'Add To' Scenarios Game

Add more arrows to your child’s math quiver by solving 'Add To' scenarios.

Find the Sum Using Part-Part-Whole Model Worksheet

Combine math learning with adventure by solving to find the sum using 'Part-Part-Whole' model.

Write Equations Using Part-Part-Whole Model Worksheet

Learn number sense at the speed of lightning by writing equations using 'Part-Part-Whole' model.

Multiplication and Division Word Problems

Select the Correct Multiplication Expression Game

Select the correct multiplication expression to play this game.

Solve the Word Problems Related to Multiplication Game

Unearth the wisdom of mathematics by learning to solve word problems related to multiplication.

Make a Model to Multiply Worksheet

Put your skills to the test by practicing to make a model to multiply.

Multiply by Making a Model Worksheet

Pack your math practice time with fun by multiplying by making a model.

Fraction Word Problems

Solve the Word Problems on Fraction Addition Game

Have your own math-themed party by learning how to solve the word problems on fraction addition.

Solve the Word Problems on Fraction Subtraction Game

Add more arrows to your child’s math quiver by solving word problems on fraction subtraction.

Word Problems on Adding Fractions & Mixed Numbers Worksheet

Become a mathematician by practicing word problems on adding fractions & mixed numbers.

Adding Fractions & Mixed Numbers Word Problems Worksheet

Help your child solve word problems on adding fractions & mixed numbers.

All Word Problems Resources

Adding One by Making a Model Game

Treat yourself to an immersive learning experience with our 'Adding One by Making a Model' game.

Solve Word Problems on Division Game

Learn to solve math problems by solving word problems on division.

Add or Subtract within 5: Summer Word Problems Worksheet

Summer-themed worksheet for students to practice adding or subtracting within 5 through word problems.

Adding Within 5 by Making a Model Game

Add more arrows to your child’s math quiver by adding within 5 by making a model.

Add or Subtract within 5: Halloween Word Problems Worksheet

Spooky-themed worksheet to practice adding and subtracting within 5 using Halloween word problems.

Solve Word Problems using Division Game

Apply your knowledge to solve word problems using division.

Model and Add (Within 10) Game

Unearth the wisdom of mathematics by learning how to model and add (within 10).

Solve Comparison Word Problems Game

Unearth the wisdom of mathematics by learning how to solve comparison word problems.

Add or Subtract within 5: Christmas Word Problems Worksheet

Fun, festive worksheet for students to practice addition and subtraction within 5, Christmas style!

Represent the Problem Using Model Worksheet

Solidify your math skills by practicing to represent the problem using models.

Solve Word Problems on Fraction-Whole Number Multiplication Game

Apply your knowledge to solve word problems on fraction-whole number multiplication.

Word Problems: Subtracting One Game

Sharpen your math skills with the 'Word Problems: Subtracting One' game.

Addition Problems Involving Mixed Numbers Worksheet

Solidify your math skills by practicing addition problems involving mixed numbers.

Add or Subtract within 5: Shopping Word Problems Worksheet

This worksheet features shopping-themed word problems, requiring addition or subtraction within 5.

Word Problems: Subtracting Within 10 Game

Enjoy the marvel of math-multiverse by practicing to solve word problems on subtracting within 10.

Represent Word Problems Worksheet

This downloadable worksheet is designed to practice representing word problems.

Real Life Problems on Adding Mixed Numbers Worksheet

Boost your ability to solve real life problems on adding mixed numbers with this fun worksheet.

Add or Subtract within 5: Travel Word Problems Worksheet

Engaging travel-themed worksheet focused on solving addition and subtraction problems within 5.

Word Problems on Equal Groups Worksheet

Assess your math skills by solving word problems on equal groups in this worksheet.

Solve Word Problems Related to Multiplicative Comparison Game

Use your math skills to solve word problems related to multiplicative comparison.

Story Problems on Subtracting Fractions Worksheet

Focus on core math skills with this worksheet by solving story problems on subtracting fractions.

Add or Subtract within 5: Sports Word Problems Worksheet

Engaging sports-themed worksheet focusing on solving addition and subtraction problems within 5.

Solve Word Problems Related to Division Game

Add more arrows to your child’s math quiver by solving word problems related to division.

Represent 'Put Together' Scenarios Game

Have your own math-themed party by learning how to represent 'Put Together' scenarios.

Word Problems on Arrays Worksheet

Help your child revise multiplication by solving word problems on arrays.

Real Life Problems on Subtracting Fractions Worksheet

In this worksheet, learners will get to solve real life problems on subtracting fractions.

Solve 'Put Together' Scenarios Game

Shine bright in the math world by learning how to solve 'Put Together' scenarios.

Represent 'Take Apart' Scenarios Game

Kids must represent 'Take Apart' scenarios to practice subtraction.

Add or Subtract within 5: Cooking Word Problems Worksheet

Engage in this fun cooking-themed worksheet, solving addition or subtraction problems within 5!

Word Problems on Comparison Worksheet

Pack your math practice time with fun by solving word problems on comparison.

Solve 'Take Apart' Scenarios Game

Take the pressure off by simplifying subtraction by solving 'Take Apart' scenarios.

Solve Count On Scenarios Game

Begin the exciting journey of becoming a math wizard by learning how to solve count on scenarios.

Subtraction Problems Involving Mixed Numbers Worksheet

Reinforce math concepts by practicing subtraction problems involving mixed numbers.

Add or Subtract within 5: Winter Word Problems Worksheet

Engaging winter-themed worksheet for students to practice addition and subtraction within 5.

Solve 'Change Unknown' Scenarios Game

Begin the exciting journey of becoming a math wizard by solving 'Change Unknown' scenarios.

Solve 'Count On' Word Problems Game

Take the first step towards building your math castle by solving 'Count On' word problems.

Solve Using Your Own Numbers Worksheet

Print this worksheet to practice solving using your own numbers like a math legend!

Real Life Problems on Subtracting Mixed Numbers Worksheet

Pack your math practice time with fun by solving real life problems on subtracting mixed numbers.

Your one stop solution for all grade learning needs.

• Entertainment

Canary Islands holiday warning: UK tourists issued travel warning as Morocco sends 'warships'

A Canary Island travel warning has been issued due to Moroccos’ military activities with warships sending a two-word warning.

The Canary Islands are bracing for potential disruptions to their peace and tourism due to Morocco's military offensive.

In March 2023, Spanish Foreign Minister Jose Manuel Albares remarked on the strengthened ties between Morocco and Spain, citing a new pinnacle in their relationship.

In a recent speech to the Spanish Senate, Albares stressed the importance of maintaining Spain’s relationship with Morocco as a top priority in its foreign and state policies.

The manoeuvres come in the context of escalating regional tensions and increasing interest in maritime security, especially in areas of strategic importance such as the Strait of Gibraltar and the Canary Islands.

Lanzarote, Tenerife and other island holidaymakers have been warned over the military activities.

The president of the Cabildo of Gran Canaria, Antonio Morales, has voiced staunch opposition to Morocco's planned military manoeuvres off the coast of Western Sahara.

He said: "The area of northwest Africa and the Canary Islands in particular need actions of peace and to flee from any message of militarisation”.

Willenhall road cordoned off after 'major incident' involving bin lorry Willenhall | 1 hour ago

West Bromwich stabbing: 13-year-old arrested on suspicion of murdering boy, 15 Crime | 1 hour ago

Lanzarote holidays: UK tourists issued holiday warning as Canary Island 'on brink of collapse' amid anti-tourism protests Travel | 8 hours ago

Watch: Disused Walsall pub flattened to make way for new Lidl store Plus Business | 11 hours ago

'Another mum without her son. Heartbreaking' – Tributes flood in for 15-year-old Isaac Brown stabbed to death in West Bromwich West Bromwich | 7 hours ago