knight tour problem statement

• Practice Backtracking
• Interview Problems on Backtracking
• MCQs on Backtracking
• Tutorial on Backtracking
• Backtracking vs Recursion
• Backtracking vs Branch & Bound
• Print Permutations
• Subset Sum Problem
• N-Queen Problem
• Knight's Tour
• Sudoku Solver
• Rat in Maze
• Hamiltonian Cycle
• Graph Coloring
• Backtracking Algorithm
• Introduction to Backtracking - Data Structure and Algorithm Tutorials
• Difference between Backtracking and Branch-N-Bound technique
• What is the difference between Backtracking and Recursion?

Standard problems on backtracking

• The Knight's tour problem
• Rat in a Maze
• N Queen Problem
• Subset Sum Problem using Backtracking
• M-Coloring Problem
• Algorithm to Solve Sudoku | Sudoku Solver
• Magnet Puzzle
• Remove Invalid Parentheses
• A backtracking approach to generate n bit Gray Codes
• Permutations of given String

Easy Problems on Backtracking

• Print all subsets of a given Set or Array
• Check if a given string is sum-string
• Count all possible Paths between two Vertices
• Find all distinct subsets of a given set using BitMasking Approach
• Find if there is a path of more than k length from a source
• Print all paths from a given source to a destination
• Print all possible strings that can be made by placing spaces

Medium prblems on Backtracking

• 8 queen problem
• Combinational Sum
• Warnsdorff's algorithm for Knight’s tour problem
• Find paths from corner cell to middle cell in maze
• Find Maximum number possible by doing at-most K swaps
• Rat in a Maze with multiple steps or jump allowed
• N Queen in O(n) space

Hard problems on Backtracking

• Power Set in Lexicographic order
• Word Break Problem using Backtracking
• Partition of a set into K subsets with equal sum
• Longest Possible Route in a Matrix with Hurdles
• Find shortest safe route in a path with landmines
• Printing all solutions in N-Queen Problem
• Print all longest common sub-sequences in lexicographical order
• Top 20 Backtracking Algorithm Interview Questions

The Knight’s tour problem

Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems that are typically solved using the backtracking technique have the following property in common. These problems can only be solved by trying every possible configuration and each configuration is tried only once. A Naive solution for these problems is to try all configurations and output a configuration that follows given problem constraints. Backtracking works incrementally and is an optimization over the Naive solution where all possible configurations are generated and tried. For example, consider the following Knight’s Tour problem. 

Problem Statement: Given a N*N board with the Knight placed on the first block of an empty board. Moving according to the rules of chess knight must visit each square exactly once. Print the order of each cell in which they are visited.

The path followed by Knight to cover all the cells Following is a chessboard with 8 x 8 cells. Numbers in cells indicate the move number of Knight. 

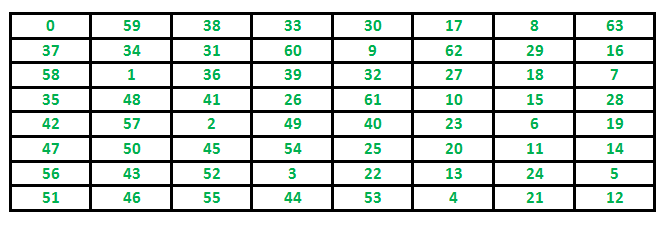
Let us first discuss the Naive algorithm for this problem and then the Backtracking algorithm.

Naive Algorithm for Knight’s tour   The Naive Algorithm is to generate all tours one by one and check if the generated tour satisfies the constraints. 

Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In the context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives works out then we go to the previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.

Backtracking Algorithm for Knight’s tour  

Following is the Backtracking algorithm for Knight’s tour problem. 

Following are implementations for Knight’s tour problem. It prints one of the possible solutions in 2D matrix form. Basically, the output is a 2D 8*8 matrix with numbers from 0 to 63 and these numbers show steps made by Knight.   

Time Complexity :  There are N 2 Cells and for each, we have a maximum of 8 possible moves to choose from, so the worst running time is O(8 N^2 ).

Auxiliary Space: O(N 2 )

Important Note: No order of the xMove, yMove is wrong, but they will affect the running time of the algorithm drastically. For example, think of the case where the 8th choice of the move is the correct one, and before that our code ran 7 different wrong paths. It’s always a good idea a have a heuristic than to try backtracking randomly. Like, in this case, we know the next step would probably be in the south or east direction, then checking the paths which lead their first is a better strategy.

Note that Backtracking is not the best solution for the Knight’s tour problem. See the below article for other better solutions. The purpose of this post is to explain Backtracking with an example.  Warnsdorff’s algorithm for Knight’s tour problem

References:  http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf   http://www.cis.upenn.edu/~matuszek/cit594-2009/Lectures/35-backtracking.ppt   http://mathworld.wolfram.com/KnightsTour.html   http://en.wikipedia.org/wiki/Knight%27s_tour    

Please Login to comment...

Similar reads.

• chessboard-problems
• Backtracking
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Welcome.please sign up.

By signing up or logging in, you agree to our Terms of service and confirm that you have read our Privacy Policy .

Already a member? Go to Log In

Welcome.please login.

Forgot your password

Not registered yet? Go to Sign Up

• Introduction
• Analyze Your Algorithm
• Growth of a Function
• Analyze Iterative Algorithms
• Recurrences
• Let's Iterate
• Now the Recursion
• Master's Theorem
• Sort It Out
• Bubble Sort
• Count and Sort
• Divide and Conquer
• Binary Search
• Dynamic Programming
• Knapsack Problem
• Rod Cutting
• Coin Change
• Backtracking
• Knight's Tour Problem
• Greedy Algorithm
• Activity Selection
• Egyptian Fraction
• Huffman Codes
• Minimum Spanning Tree
• Prim's Algorithm

Knight's Tour Problem | Backtracking

In the previous example of backtracking , you have seen that backtracking gave us a $O(n!)$ running time. Generally, backtracking is used when we need to check all the possibilities to find a solution and hence it is expensive. For the problems like N-Queen and Knight's tour, there are approaches which take lesser time than backtracking, but for a small size input like 4x4 chessboard, we can ignore the running time and the backtracking leads us to the solution.

Knight's tour is a problem in which we are provided with a NxN chessboard and a knight.

For a person who is not familiar with chess, the knight moves two squares horizontally and one square vertically, or two squares vertically and one square horizontally as shown in the picture given below.

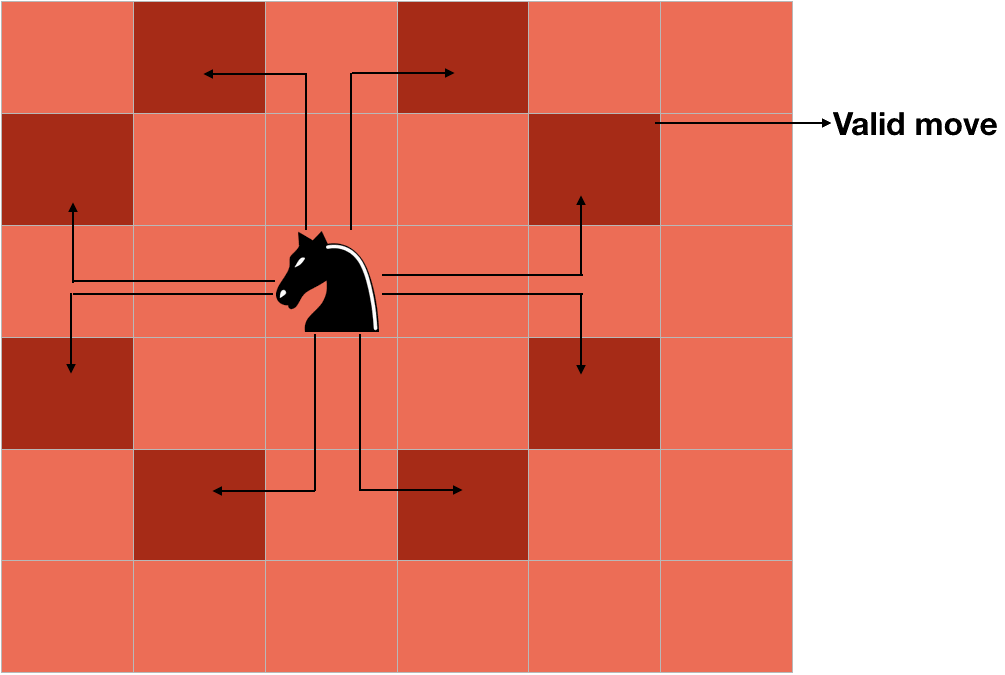
Thus if a knight is at (3, 3), it can move to the (1, 2) ,(1, 4), (2, 1), (4, 1), (5, 2), (5, 4), (2, 5) and (4, 5) cells.

Thus, one complete movement of a knight looks like the letter "L", which is 2 cells long.

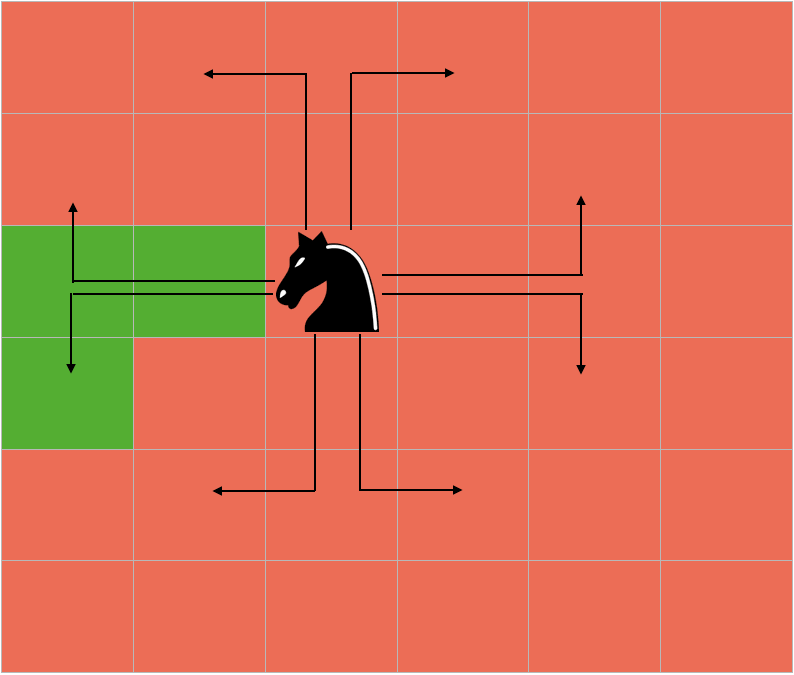
According to the problem, we have to make the knight cover all the cells of the board and it can move to a cell only once.

There can be two ways of finishing the knight move - the first in which the knight is one knight's move away from the cell from where it began, so it can go to the position from where it started and form a loop, this is called closed tour ; the second in which the knight finishes anywhere else, this is called open tour .

Approach to Knight's Tour Problem

Similar to the N-Queens problem, we start by moving the knight and if the knight reaches to a cell from where there is no further cell available to move and we have not reached to the solution yet (not all cells are covered), then we backtrack and change our decision and choose a different path.

So from a cell, we choose a move of the knight from all the moves available, and then recursively check if this will lead us to the solution or not. If not, then we choose a different path.

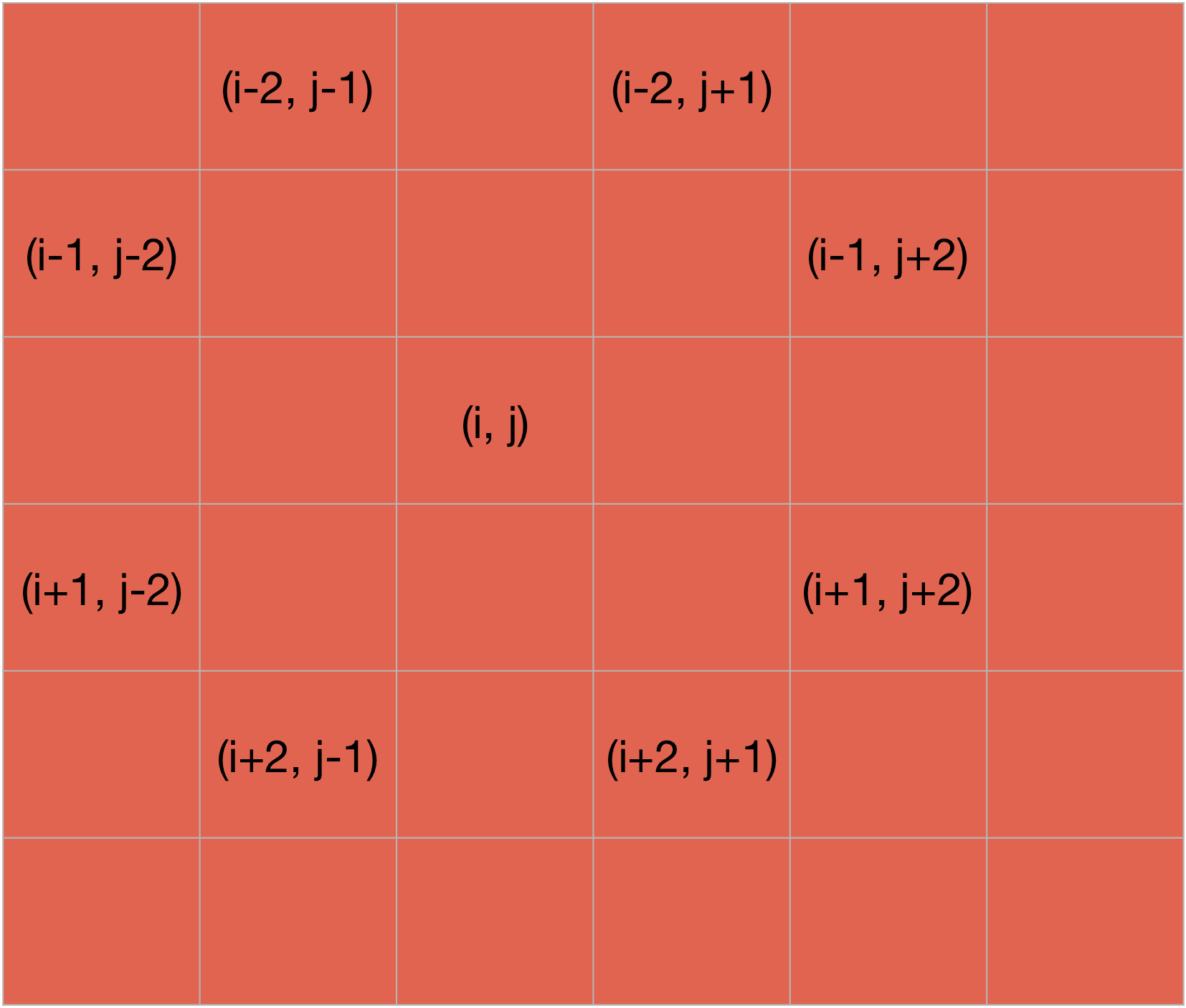
As you can see from the picture above, there is a maximum of 8 different moves which a knight can take from a cell. So if a knight is at the cell (i, j), then the moves it can take are - (i+2, j+1), (i+1, j+2), (i-2,j+1), (i-1, j+2), (i-1, j-2), (i-2, j-1), (i+1, j-2) and (i+2, j-1).

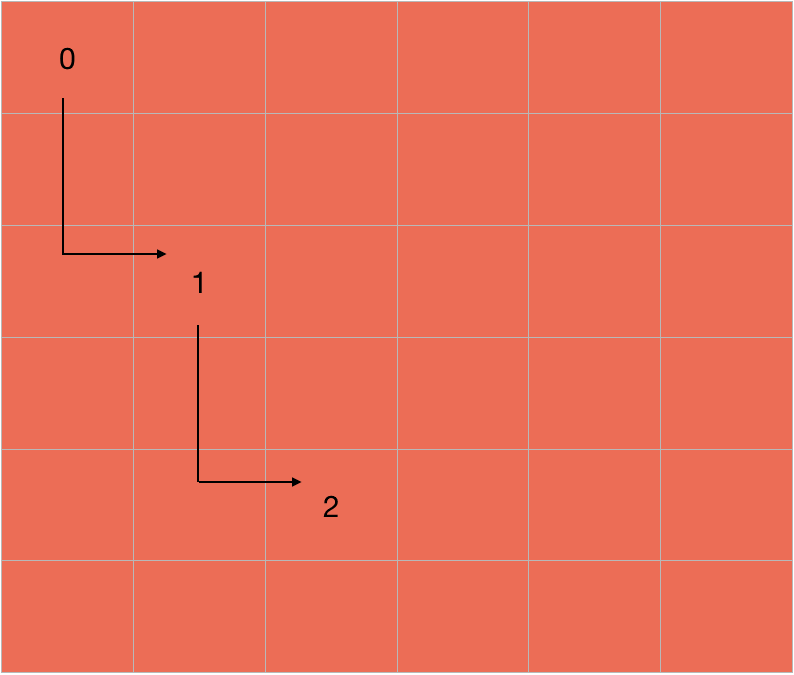
We keep the track of the moves in a matrix. This matrix stores the step number in which we visited a cell. For example, if we visit a cell in the second step, it will have a value of 2.

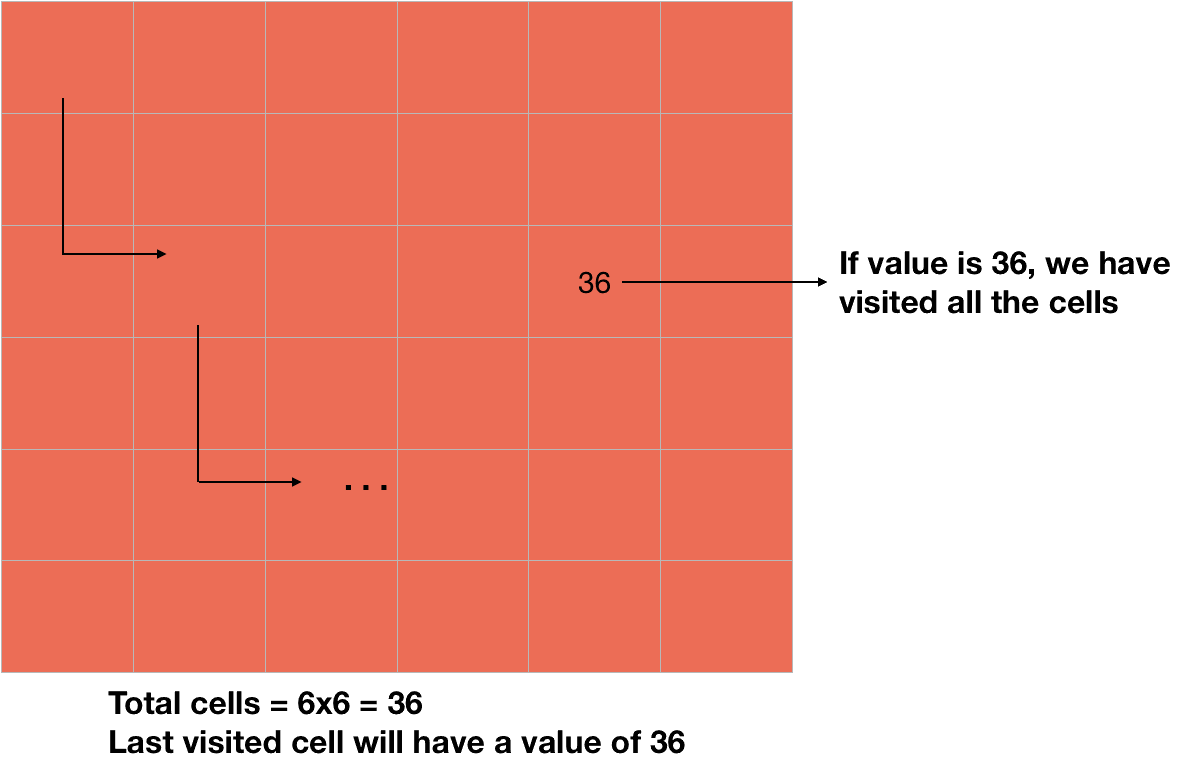
This matrix also helps us to know whether we have covered all the cells or not. If the last visited cell has a value of N*N, it means we have covered all the cells.

Thus, our approach includes starting from a cell and then choosing a move from all the available moves. Then we check if this move will lead us to the solution or not. If not, we choose a different move. Also, we store all the steps in which we are moving in a matrix.

Now, we know the basic approach we are going to follow. So, let's develop the code for the same.

Code for Knight's Tour

Let's start by making a function to check if a move to the cell (i, j) is valid or not - IS-VALID(i, j, sol) . As mentioned above, 'sol' is the matrix in which we are storing the steps we have taken.

A move is valid if it is inside the chessboard (i.e., i and j are between 1 to N) and if the cell is not already occupied (i.e., sol[i][j] == -1 ). We will make the value of all the unoccupied cells equal to -1.

As stated above, there is a maximum of 8 possible moves from a cell (i, j). Thus, we will make 2 arrays so that we can use them to check for the possible moves.

Thus if we are on a cell (i, j), we can iterate over these arrays to find the possible move i.e., (i+2, j+1), (i+1, j+2), etc.

Now, we will make a function to find the solution. This function will take the solution matrix, the cell where currently the knight is (initially, it will be at (1, 1)), the step count of that cell and the two arrays for the move as mentioned above - KNIGHT-TOUR(sol, i, j, step_count, x_move, y_move) .

We will start by checking if the solution is found. If the solution is found ( step_count == N*N ), then we will just return true.

KNIGHT-TOUR(sol, i, j, step_count, x_move, y_move)   if step_count == N*N     return TRUE

Our next task is to move to the next possible knight's move and check if this will lead us to the solution. If not, then we will select the different move and if none of the moves are leading us to the solution, then we will return false.

As mentioned above, to find the possible moves, we will iterate over the x_move and the y_move arrays.

KNIGHT-TOUR(sol, i, j, step_count, x_move, y_move)   ...   for k in 1 to 8     next_i = i+x_move[k]     next_j = j+y_move[k]

Now, we have to check if the cell (i+x_move[k], j+y_move[k]) is valid or not. If it is valid then we will move to that cell - sol[i+x_move[k]][j+y_move[k]] = step_count and check if this path is leading us to the solution ot not - if KNIGHT-TOUR(sol, i+x_move[k], j+y_move[k], step_count+1, x_move, y_move) .

KNIGHT-TOUR(sol, i, j, step_count, x_move, y_move)   ...   for k in 1 to 8     ...     if IS-VALID(i+x_move[k], j+y_move[k])       sol[i+x_move[k]][j+y_move[k]] = step_count       if KNIGHT-TOUR(sol, i+x_move[k], j+y_move[k], step_count+1, x_move, y_move)         return TRUE

If the move (i+x_move[k], j+y_move[k]) is leading us to the solution - if KNIGHT-TOUR(sol, i+x_move[k], j+y_move[k], step_count+1, x_move, y_move) , then we are returning true.

If this move is not leading us to the solution, then we will choose a different move (loop will iterate to a different move). Also, we will again make the cell (i+x_move[k], j+y_move[k]) of solution matrix -1 as we have checked this path and it is not leading us to the solution, so leave it and thus it is backtracking.

KNIGHT-TOUR(sol, i, j, step_count, x_move, y_move)   ...   for k in 1 to 8     ...       sol[i+x_move[k], j+y_move[k]] = -1

At last, if none the possible move returns us false, then we will just return false.

We have to start the KNIGHT-TOUR function by passing the solution, x_move and y_move matrices. So, let's do this.

As stated earlier, we will initialize the solution matrix by making all its element -1.

for i in 1 to N   for j in 1 to N     sol[i][j] = -1

The next task is to make x_move and y_move arrays.

x_move = [2, 1, -1, -2, -2, -1, 1, 2] y_move = [1, 2, 2, 1, -1, -2, -2, -1]

We will start the tour of the knight from the cell (1, 1) as its first step. So, we will make the value of the cell(1, 1) 0 and then call KNIGHT-TOUR(sol, 1, 1, 1, x_move, y_move) .

Analysis of Code

We are not going into the full time complexity of the algorithm. Instead, we are going to see how bad the algorithm is.

There are N*N i.e., N 2 cells in the board and we have a maximum of 8 choices to make from a cell, so we can write the worst case running time as $O(8^{N^2})$.

But we don't have 8 choices for each cell. For example, from the first cell, we only have two choices.

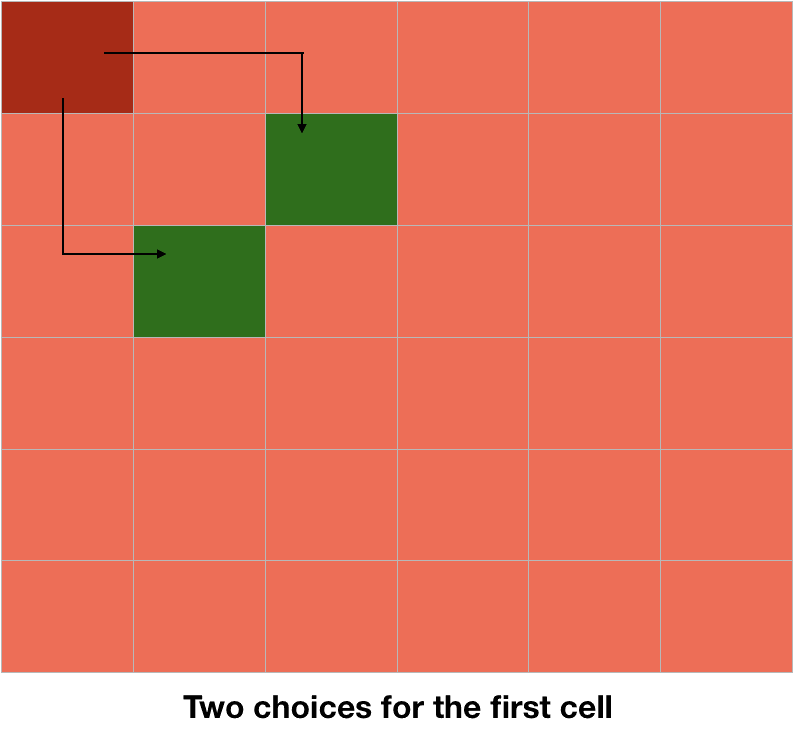
Even considering this, our running time will be reduced by a factor and will become $O(k^{N^2})$ instead of $O(8^{N^2})$. This is also indeed an extremely bad running time.

So, this chapter was to make you familiar with the backtracking algorithm and not about the optimization. You can look for more examples on the backtracking algorithm with the backtracking tag of the BlogsDope .

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Knight's tour problem

What is knight's tour problem.

In the knight's tour problem, we are given with an empty chess board of size NxN, and a knight. In chess, the knight is a piece that looks exactly like a horse. Assume, it can start from any location on the board. Now, our task is to check whether the knight can visit all of the squares on the board or not. When it can visit all of the squares, then print the number of jumps needed to reach that location from the starting point.

There can be two ways in which a knight can finish its tour. In the first way, the knight moves one step and returns back to the starting position forming a loop which is called a closed tour . In the second way i.e. the open tour , it finishes anywhere in the board.

For a person who is not familiar with chess, note that the knight moves in a special manner. It can move either two squares horizontally and one square vertically or two squares vertically and one square horizontally in each direction. So, the complete movement looks like English letter 'L' .

Suppose the size of given chess board is 8 and the knight is at the top-left position on the board. The next possible moves are shown below −

Each cell in the above chess board holds a number, that indicates where to start and in how many moves the knight will reach a cell. The final values of the cell will be represented by the below matrix −

Remember, this problem can have multiple solutions, the above matrix is one possible solution.

One way to solve the knight's tour problem is by generating all the tours one by one and then checking if they satisfy the specified constraint or not. However, it is time consuming and not an efficient way.

Backtracking Approach to Solve Knight's tour problem

The other way to solve this problem is to use backtracking. It is a technique that tries different possibilities until a solution is found or all options are tried. It involves choosing a move, making it, and then recursively trying to solve the rest of the problem. If the current move leads to a dead end, we backtrack and undo the move, then try another one.

To solve the knight's tour problem using the backtracking approach, follow the steps given below −

Start from any cell on the board and mark it as visited by the knight.

Move the knight to a valid unvisited cell and mark it visited. From any cell, a knight can take a maximum of 8 moves.

If the current cell is not valid or not taking to the solution, then backtrack and try other possible moves that may lead to a solution.

Repeat this process until the moves of knight are equal to 8 x 8 = 64.

In the following example, we will practically demonstrate how to solve the knight's tour problem.

• [email protected]

What’s New ?

The Top 10 favtutor Features You Might Have Overlooked

• Don’t have an account Yet? Sign Up

Remember me Forgot your password?

• Already have an Account? Sign In

Lost your password? Please enter your email address. You will receive a link to create a new password.

Back to log-in

By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.

The Knight's Tour Problem (using Backtracking Algorithm)

• Jun 30, 2023
• 6 Minute Read
• Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
• By Vedanti Kshirsagar

Ever wondered how a computer playing as a chess player improves its algorithm to defeat you in the game? In this article, we will learn about the Knight's Tour Problem, the various ways to solve it along with their time and space complexities. So, let's get started!

What is Knight's Tour Problem?

Just for a reminder, the knight is a piece in chess that usually looks like a horse and moves in an L-shaped pattern. This means it will first move two squares in one direction and then one square in a perpendicular direction.

The Knight's Tour problem is about finding a sequence of moves for the knight on a chessboard such that it visits every square on the board exactly one time. It is a type of Hamiltonian path problem in graph theory, where the squares represent the vertices and the knight's moves represent the edges of the graph.

This problem has fascinated many mathematicians for centuries, but the solutions they found were very difficult. The simple solution will be to find every conceivable configuration and selecting the best one is one technique to solve this problem. But that will take a load of time.

One popular solution to solve the Knight's tour problem is Warnsdorff's rule, which involves choosing the next move that leads to a square with the fewest available moves. There is also a backtracking approach. 

 But first moving to all that, let's take a quick understanding of the Hamiltonian path problem.

Hamiltonian Path Problem

The Hamiltonian path problem is a well-known problem in graph theory that asks whether a given graph contains a path that visits every vertex exactly once.

A path that visits every vertex exactly once is called a Hamiltonian path, and a graph that contains a Hamiltonian path is called a Hamiltonian graph. 

Let's take an example of the Hamiltonian path problem. Suppose we have a graph with five vertices and the following edges:

This graph can be represented as:

Knight's Tour Backtracking Algorithm

The backtracking algorithm works by exploring all possible moves for the knight, starting from a given square, and backtracking to try different moves if it reaches a dead end.

Here's the basic outline of the backtracking algorithm to solve the Knight's tour problem:

• Choose a starting square for the knight on the chessboard.
• Mark the starting square as visited.
• For each valid move from the current square, make the move and recursively repeat the process for the new square.
• If all squares on the chessboard have been visited, we have found a solution. Otherwise, undo the last move and try a different move.
• If all moves have been tried from the current square and we have not found a solution, backtrack to the previous square and try a different move from there.
• If we have backtracked to the starting square and tried all possible moves without finding a solution, there is no solution to the problem.

We have given the full C++ program for Backtracking Algorithm to solve Knight's Tour Problem below:

Check the image below before we explain the code:

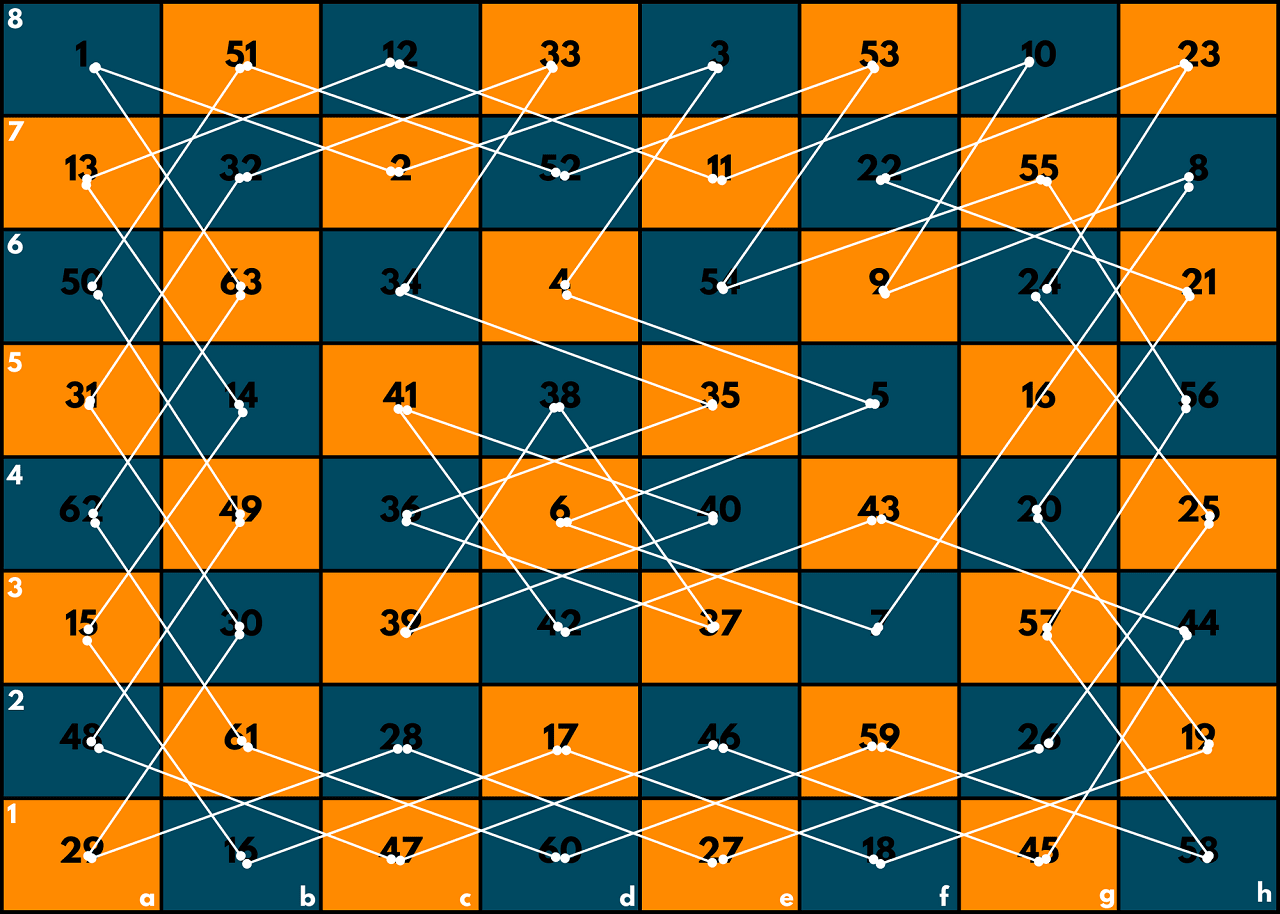
In this implementation, we first define a function validMoves  which takes the current row and column of the knight as input and returns a vector of pairs representing all the valid moves that the knight can make from that position.

The solve function is a recursive function that takes the current row and column of the knight, as well as the current move number, as input. We mark the current square as visited by setting board[row][column] it to the current move number, and then we recursively try all possible moves from the current position.

If we reach the last move, then we found a solution and return true. If no valid move is found from the current position, we backtrack by setting the current square to 0 and returning false.

In the main function, we start the solve function at a specified starting position and then output the number of moves it took to find a solution and print the final chessboard with the solution.

Time & Space Complexity for Backtracking

The backtracking algorithm used to solve the Knight's Tour problem has an exponential time complexity. The number of possible paths for the knight grows very quickly as the size of the chessboard increases, which means that the time taken to explore all possible paths grows exponentially.

The exact time complexity of the Knight's Tour Backtracking algorithm is O(8^(n^2)), where n is the size of the chessboard. This is because each move has a maximum of 8 possible directions, and we have to explore all possible moves until we find a solution.

The space complexity of the backtracking algorithm is O(n^2), where n is the size of the chessboard. So, we can say that the backtracking algorithm is efficient for smaller chessboards.

Warnsdorff's Rule

Warndorff's rule is a heuristic greedy algorithm used to solve this problem. It tries to move the knight to the square with the fewest valid moves, hoping that this will lead to a solution.

Here's an overview of how Warndorff's rule algorithm works:

• Start with a random square on the chessboard.
• From the current square, consider all possible moves and count the number of valid moves from each adjacent square.
• Move to the square with the lowest number of valid moves. In case of a tie, move to the square with the lowest number of valid moves from its adjacent squares.
• Repeat steps 2 and 3 until all squares on the chessboard have been visited.

Here is the pseudocode for Warndorff's rule algorithm:

The time complexity of Warndorff's rule algorithm is O(n^2 log n), where n is the size of the chessboard. This is because we have to visit each square once, and for each square, we have to compute the number of valid moves from each adjacent square. The space complexity of the algorithm is O(n^2) since we need to store the chessboard and the current position of the knight.

Overall, The Knight's Tour problem is related to chess, and solving it can help chess players improve their strategy and become better at the game. In the real world, you can also use it to design efficient algorithms for finding the shortest path between two points in a network.

Now we know The Knight's Tour Problem and its solutions using Backtracking and Warnsdorff's Rule. It has several applications in various fields such as Game theory, Network Routing etc, making it an important problem to study in computer science and mathematics.

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Vedanti Kshirsagar

More by favtutor blogs, monte carlo simulations in r (with examples), aarthi juryala.

The unlist() Function in R (with Examples)

Paired Sample T-Test using R (with Examples)

Python Tutorial

Python oops, python mysql, python mongodb, python sqlite, python questions, python tkinter (gui), python web blocker, related tutorials, python programs.

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Warnsdorff’s algorithm for knight’s tour problem

Warnsdorff’s algorithm are used to find all moves of single knight's tour. This algorithm is start with a random position of the cell in the [8X8] grid. And check whether the knight can be visit other all points in grid or not.

When knight is not visit to each cell, Then using of backtracking change the path of knight. If its solution is not possible then change starting position are repeat same process until solution are not found.

This algorithm work on random number selection so result can different. Here given code implementation process.

Problem Statement

Given an N x N chessboard, the task is to find a sequence of moves for a knight such that it visits every square exactly once. The knight follows the rules of chess for its movements, i.e., it moves in an L-shape (two squares horizontally or vertically and then one square in the perpendicular direction).

Pseudocode Algorithm with Explanation

• Initialize the chessboard matrix with -1's. This matrix will represent the knight's tour.
• Choose a random starting location (sx, sy) on the chessboard.
• Set the value of the first move at position (x, y) to 1.
• Iterate (N * N) - 1 times to make the remaining moves:
• Use the move_process function to determine the next valid move based on Warnsdorff's heuristic.
• If there are no valid moves, return 0 to indicate that a valid knight's tour cannot be found.
• Update the knight's position (x, y) to the chosen move.
• Check if the last position has a valid move back to the starting position. If not, return 0.
• Print the resulting knight's tour.
• Return 1 to indicate that a valid knight's tour has been found.

Code Solution

Resultant output explanation.

The resultant output represents a valid knight's tour on an 8x8 chessboard. Each number corresponds to the move number of the knight. The knight starts at position (5, 5) and follows a sequence of moves until it visits all the squares of the chessboard exactly once. The numbers are arranged in the order of the knight's moves.

Time Complexity of the Code

The time complexity of Warnsdorff's algorithm for the knight's tour problem is O(N^2) in the worst case. This is because the algorithm performs a constant number of operations for each square on the chessboard, which has a total of N^2 squares.

Please share your knowledge to improve code and content standard. Also submit your doubts, and test case. We improve by your feedback. We will try to resolve your query as soon as possible.

New Comment

• Single linked list
• Backtracking

Exploring the Knight’s Tour Problem

The Knight’s tour problem is an interesting and challenging puzzle that has fascinated mathematicians for centuries. The problem is to find a sequence of moves for a knight on a chessboard such that the knight visits every square exactly once. This problem has been studied since the 9th century, and has been the subject of much research and speculation.

One of the most interesting aspects of the Knight’s tour problem is that it is not always possible to find a solution. This is because the knight’s movement is constrained by the geometry of the chessboard, and some configurations simply do not allow for a complete tour. However, it has been proven that a Knight’s tour is always possible on a rectangular board whose smaller dimension is at least 5.

For any m x n board with m ≤ n, a Knight’s tour is always possible unless one or more of thee three conditions are met: m = 1 or 2. m = 3 and n = 3, 5, or 6. This means that for most standard chessboards, a Knight’s tour is possible.

However, there are some exceptions to this rule. For example, if a square is removed from the chessboard, it may no longer be possible to find a complete Knight’s tour. This is because the removal of a single square can disrupt the geometry of the chessboard in such a way that it becomes impossible to visit every square.

Despite these challenges, the Knight’s tour problem remains a popular puzzle among mathematicians and puzzle enthusiasts. It is a fascinating example of how mathematics can be used to explore complex problems in a structured and systematic way.

The Knight’s tour problem is an intriguing puzzle that continues to fascinate mathematicians and puzzle enthusiasts alike. While there are some situations where it may not be possible to find a complete tour, the problem remains a challenging and rewarding pursuit for those who enjoy puzzles and problem-solving.

Is The Knight’s Tour Possible?

The Knight’s Tour is possible on a rectangular board whose smaller dimension is at least 5. Additionally, for any m x n board with m ≤ n, a Knight’s Tour is always possible unless one of the following conditions are met: – m = 1 or 2 – m = 3 and n = 3, 5, or 6.

It is important to note that a Knight’s Tour is a sequence of moves made by a knight on a chessboard, where the knight visits every square exactly once. The proof of the existence of a Knight’s Tour on certain types of boards is a well-studied problem in mathematics.

What Is The Knights Tour Theory?

The Knight’s tour theory is a problem in the field of mathematics and chess. The problem is to find a sequence of moves by a knight on a chessboard such that the knight visits every square exactly once. The knight is allowed to move two squares in one direction and one square in the perpendicular direction. The problem has been studied for centuries, and many different solutions have been proposed.

One of the main questions in the Knight’s tour theory is whether a knight’s tour exists for every possible starting position and board size. It has been proven that a knight’s tour exists on all chessboards with one square removed, except for some specific cases. For example, if the board size is even, or if the removed square is (i, j) with i + j odd, then a knight’s tour may not be possible.

Other specific cases whre a knight’s tour may not be possible include when the board size is 3 and any square other than the center square is removed, when the board size is 5, when the board size is 7 and any square other than square (2, 2) or (2, 6) is removed, and when the board size is 9 and a certain specific square is removed.

The Knight’s tour theory is a fascinating problem that has captured the imagination of mathematicians and chess players alike. It is a challenging problem that requires creative thinking and careful analysis, and it continues to be studied and explored by researchers today.

What Is The Knight’s Tour Problem?

The Knight’s Tour problem is a mathematical puzzle that requires a player to find a sequence of moves for a knight piece on a chessboard, such that the knight visits every square exactly once. In other words, the problem asks whethr a knight can move to every square on the chessboard without repeating any square. The knight is allowed to move only in an L-shaped pattern, i.e., two squares horizontally or vertically and then one square in the perpendicular direction. The problem has been studied for centuries and has fascinated mathematicians and chess players alike. It has many applications in computer science, such as in algorithm design and optimization. The Knight’s Tour problem is a classic example of a combinatorial optimization problem, and finding a solution to the problem requires a lot of creativity and strategic planning.

The Knight’s tour problem has been a topic of interest for mathematicians and chess enthusiasts for centuries. While the problem may seem simple at first glance, it presents a challenging puzzle that requires careful analysis and strategic thinking. Through the years, various algorithms and techniques have been developed to solve the problem, and it has been proven that a Knight’s tour is possible on crtain types of chessboards. However, some conditions must be met, and certain squares must not be removed for the tour to be achievable. Despite its difficulty, the Knight’s tour problem remains a fascinating and engaging puzzle that continues to capture the imagination of people from all walks of life.

Doug Barlow

Help | Advanced Search

Mathematics > Combinatorics

Title: proving the existence of euclidean knight's tours on $n \times n \times \cdots \times n$ chessboards for $n < 4$.

Abstract: The Knight's Tour problem consists of finding a Hamiltonian path for the knight on a given set of points so that the knight can visit exactly once every vertex of the mentioned set. In the present paper, we provide a $5$-dimensional alternative to the well-known statement that it is not ever possible for a knight to visit once every vertex of $C(3,k) := \{0,1,2\}^k$ by performing a sequence of $3^k-1$ jumps of standard length, since the most accurate answer to the original question actually depends on which mathematical assumptions we are making at the beginning of the game, when we decide to extend a planar chess piece to the third dimension and above. Our counterintuitive outcome follows from the observation that we can alternatively define a $2$D knight as a piece that moves from one square to another on the chessboard by covering a fixed Euclidean distance of $\sqrt{5}$ so that also the statement of Theorem~3 in [Erde, J., Gol{é}nia, B., \& Gol{é}nia, S. (2012), The closed knight tour problem in higher dimensions, The Electronic Journal of Combinatorics, 19(4), \#P9] does not hold anymore for such a Euclidean knight, as long as a $2 \times 2 \times \cdots \times 2$ chessboard with at least $2^6$ cells is given. Moreover, we show a classical closed knight's tour on $C(3,4)-\{(1,1,1,1)\}$ whose arrival is at a distance of $2$ from $(1,1,1,1)$, and we finally construct closed Euclidean knight's tours on $\{0,1\}^k$ for each integer $k \geq 6$.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

1 blog link

Bibtex formatted citation.

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .