travelling salesman map

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

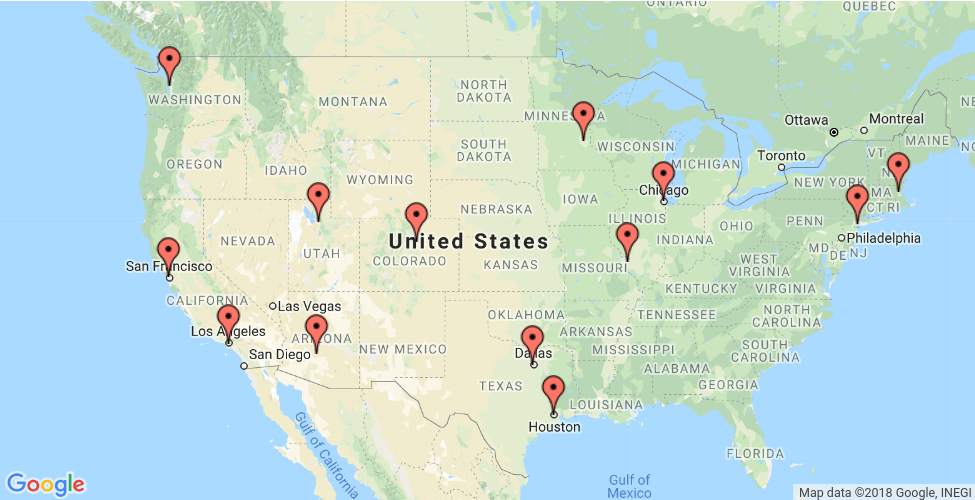
The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

• The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
• The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

• The number of rows of the distance matrix, which is the number of locations (including the depot).
• The number of vehicles in the problem.
• The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices, from_index and to_index , and returns the corresponding entry of the distance matrix.

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

Traveling Salesman Problem

The traveling salesman problem (TSP) asks the question, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?".

This project

• The goal of this site is to be an educational resource to help visualize, learn, and develop different algorithms for the traveling salesman problem in a way that's easily accessible
• As you apply different algorithms, the current best path is saved and used as input to whatever you run next. (e.g. shortest path first -> branch and bound). The order in which you apply different algorithms to the problem is sometimes referred to the meta-heuristic strategy.

Heuristic algorithms

Heuristic algorithms attempt to find a good approximation of the optimal path within a more reasonable amount of time.

Construction - Build a path (e.g. shortest path)

• Shortest Path

Arbitrary Insertion

Furthest insertion.

• Nearest Insertion
• Convex Hull Insertion*
• Simulated Annealing*

Improvement - Attempt to take an existing constructed path and improve on it

• 2-Opt Inversion
• 2-Opt Reciprcal Exchange*

Exhaustive algorithms

Exhaustive algorithms will always find the best possible solution by evaluating every possible path. These algorithms are typically significantly more expensive then the heuristic algorithms discussed next. The exhaustive algorithms implemented so far include:

• Random Paths

Depth First Search (Brute Force)

• Branch and Bound (Cost)
• Branch and Bound (Cost, Intersections)*

Dependencies

These are the main tools used to build this site:

• web workers
• material-ui

Contributing

Pull requests are always welcome! Also, feel free to raise any ideas, suggestions, or bugs as an issue.

This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example,

• With 10 points there are 181,400 paths to evaluate.
• With 11 points, there are 1,814,000.
• With 12 points there are 19,960,000.
• With 20 points there are 60,820,000,000,000,000, give or take.
• With 25 points there are 310,200,000,000,000,000,000,000, give or take.

This is factorial growth, and it quickly makes the TSP impractical to brute force. That is why heuristics exist to give a good approximation of the best path, but it is very difficult to determine without a doubt what the best path is for a reasonably sized traveling salesman problem.

This is a recursive, depth-first-search algorithm, as follows:

• From the starting point
• For all other points not visited
• If there are no points left return the current cost/path
• Else, go to every remaining point and
• Mark that point as visited
• " recurse " through those paths (go back to 1. )

Implementation

Nearest neighbor.

This is a heuristic, greedy algorithm also known as nearest neighbor. It continually chooses the best looking option from the current state.

• sort the remaining available points based on cost (distance)
• Choose the closest point and go there
• Chosen point is no longer an "available point"
• Continue this way until there are no available points, and then return to the start.

Two-Opt inversion

This algorithm is also known as 2-opt, 2-opt mutation, and cross-aversion. The general goal is to find places where the path crosses over itself, and then "undo" that crossing. It repeats until there are no crossings. A characteristic of this algorithm is that afterwards the path is guaranteed to have no crossings.

• While a better path has not been found.
• For each pair of points:
• Reverse the path between the selected points.
• If the new path is cheaper (shorter), keep it and continue searching. Remember that we found a better path.
• If not, revert the path and continue searching.

This is an impractical, albeit exhaustive algorithm. It is here only for demonstration purposes, but will not find a reasonable path for traveling salesman problems above 7 or 8 points.

I consider it exhaustive because if it runs for infinity, eventually it will encounter every possible path.

• From the starting path
• Randomly shuffle the path
• If it's better, keep it
• If not, ditch it and keep going

This is a heuristic construction algorithm. It select a random point, and then figures out where the best place to put it will be.

• First, go to the closest point
• Choose a random point to go to
• Find the cheapest place to add it in the path
• Continue from #3 until there are no available points, and then return to the start.

Two-Opt Reciprocal Exchange

This algorithm is similar to the 2-opt mutation or inversion algorithm, although generally will find a less optimal path. However, the computational cost of calculating new solutions is less intensive.

The big difference with 2-opt mutation is not reversing the path between the 2 points. This algorithm is not always going to find a path that doesn't cross itself.

It could be worthwhile to try this algorithm prior to 2-opt inversion because of the cheaper cost of calculation, but probably not.

• Swap the points in the path. That is, go to point B before point A, continue along the same path, and go to point A where point B was.

Branch and Bound on Cost

This is a recursive algorithm, similar to depth first search, that is guaranteed to find the optimal solution.

The candidate solution space is generated by systematically traversing possible paths, and discarding large subsets of fruitless candidates by comparing the current solution to an upper and lower bound. In this case, the upper bound is the best path found so far.

While evaluating paths, if at any point the current solution is already more expensive (longer) than the best complete path discovered, there is no point continuing.

For example, imagine:

• A -> B -> C -> D -> E -> A was already found with a cost of 100.
• We are evaluating A -> C -> E, which has a cost of 110. There is no point evaluating the remaining solutions.

Instead of continuing to evaluate all of the child solutions from here, we can go down a different path, eliminating candidates not worth evaluating:

• A -> C -> E -> D -> B -> A
• A -> C -> E -> B -> D -> A

Implementation is very similar to depth first search, with the exception that we cut paths that are already longer than the current best.

This is a heuristic construction algorithm. It selects the closest point to the path, and then figures out where the best place to put it will be.

• Choose the point that is nearest to the current path

Branch and Bound (Cost, Intersections)

This is the same as branch and bound on cost, with an additional heuristic added to further minimize the search space.

While traversing paths, if at any point the path intersects (crosses over) itself, than backtrack and try the next way. It's been proven that an optimal path will never contain crossings.

Implementation is almost identical to branch and bound on cost only, with the added heuristic below:

This is a heuristic construction algorithm. It selects the furthest point from the path, and then figures out where the best place to put it will be.

• Choose the point that is furthest from any of the points on the path

Convex Hull

This is a heuristic construction algorithm. It starts by building the convex hull , and adding interior points from there. This implmentation uses another heuristic for insertion based on the ratio of the cost of adding the new point to the overall length of the segment, however any insertion algorithm could be applied after building the hull.

There are a number of algorithms to determine the convex hull. This implementation uses the gift wrapping algorithm .

In essence, the steps are:

• Determine the leftmost point
• Continually add the most counterclockwise point until the convex hull is formed
• For each remaining point p, find the segment i => j in the hull that minimizes cost(i -> p) + cost(p -> j) - cost(i -> j)
• Of those, choose p that minimizes cost(i -> p -> j) / cost(i -> j)
• Add p to the path between i and j
• Repeat from #3 until there are no remaining points

Simulated Annealing

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.

For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms

Visualize algorithms for the traveling salesman problem. Use the controls below to plot points, choose an algorithm, and control execution. (Hint: try a construction alogorithm followed by an improvement algorithm)

Programmingoneonone - Programs for Everyone

• HackerRank Problems Solutions
• _C solutions
• _C++ Solutions
• _Java Solutions
• _Python Solutions
• _Interview Preparation kit
• _1 Week Solutions
• _1 Month Solutions
• _3 Month Solutions
• _30 Days of Code
• _10 Days of JS
• CS Subjects
• _IoT Tutorials
• DSA Tutorials
• Interview Questions

HackerRank Travelling Salesman in a Grid problem solution

In this HackerRank Travelling Salesman in a Grid problem solution , The traveling salesman has a map containing m*n squares. He starts from the top left corner and visits every cell exactly once and returns to his initial position (top left). The time taken for the salesman to move from a square to its neighbor might not be the same. Two squares are considered adjacent if they share a common edge and the time is taken to reach square b from square a and vice-versa is the same. Can you figure out the shortest time in which the salesman can visit every cell and get back to his initial position?

Problem solution in Python.

Problem solution in java., problem solution in c++..

Posted by: YASH PAL

You may like these posts, post a comment.

• 10 day of javascript
• 10 days of statistics
• 30 days of code
• Codechef Solutions
• coding problems
• data structure
• hackerrank solutions
• interview prepration kit
• linux shell

Social Plugin

Subscribe us, popular posts.

HackerRank Tree: Huffman Decoding problem solution

HackerRank Cut the Tree problem solution

HackerRank Jim and the Orders problem solution

Diego Vicente

Using self-organizing maps to solve the traveling salesman problem.

The Traveling Salesman Problem is a well known challenge in Computer Science: it consists on finding the shortest route possible that traverses all cities in a given map only once. Although its simple explanation, this problem is, indeed, NP-Complete. This implies that the difficulty to solve it increases rapidly with the number of cities, and we do not know in fact a general solution that solves the problem. For that reason, we currently consider that any method able to find a sub-optimal solution is generally good enough (we cannot verify if the solution returned is the optimal one most of the times).

To solve it, we can try to apply a modification of the Self-Organizing Map (SOM) technique. Let us take a look at what this technique consists, and then apply it to the TSP once we understand it better.

Note (2018-02-01): You can also read this post in Chinese , translated by Yibing Du.

Some insight on Self-Organizing Maps

The original paper released by Teuvo Kohonen in 1998 1 consists on a brief, masterful description of the technique. In there, it is explained that a self-organizing map is described as an (usually two-dimensional) grid of nodes, inspired in a neural network. Closely related to the map, is the idea of the model , that is, the real world observation the map is trying to represent. The purpose of the technique is to represent the model with a lower number of dimensions, while maintaining the relations of similarity of the nodes contained in it.

To capture this similarity, the nodes in the map are spatially organized to be closer the more similar they are with each other. For that reason, SOM are a great way for pattern visualization and organization of data. To obtain this structure, the map is applied a regression operation to modify the nodes position in order update the nodes, one element from the model (\(e\)) at a time. The expression used for the regression is:

\[ n_{t+1} = n_{t} + h(w_{e}) \cdot \Delta(e, n_{t}) \]

This implies that the position of the node $n$ is updated adding the distance from it to the given element, multiplied by the neighborhood factor of the winner neuron, \(w_{e}\). The winner of an element is the more similar node in the map to it, usually measured by the closer node using the Euclidean distance (although it is possible to use a different similarity measure if appropriate).

On the other side, the neighborhood is defined as a convolution-like kernel for the map around the winner. Doing this, we are able to update the winner and the neurons nearby closer to the element, obtaining a soft and proportional result. The function is usually defined as a Gaussian distribution, but other implementations are as well. One worth mentioning is a bubble neighborhood, that updates the neurons that are within a radius of the winner (based on a discrete Kronecker delta function), which is the simplest neighborhood function possible.

Modifying the technique

To use the network to solve the TSP, the main concept to understand is how to modify the neighborhood function. If instead of a grid we declare a circular array of neurons , each node will only be conscious of the neurons in front of and behind it. That is, the inner similarity will work just in one dimension. Making this slight modification, the self-organizing map will behave as an elastic ring, getting closer to the cities but trying to minimize the perimeter of it thanks to the neighborhood function.

Although this modification is the main idea behind the technique, it will not work as is: the algorithm will hardly converge any of the times. To ensure the convergence of it, we can include a learning rate, \(\alpha\), to control the exploration and exploitation of the algorithm. To obtain high exploration first, and high exploitation after that in the execution, we must include a decay in both the neighborhood function and the learning rate. Decaying the learning rate will ensure less aggressive displacement of the neurons around the model, and decaying the neighborhood will result in a more moderate exploitation of the local minima of each part of the model. Then, our regression can be expressed as:

\[ n_{t+1} = n_{t} + \alpha_{t} \cdot g(w_{e}, h_{t}) \cdot \Delta(e, n_{t}) \]

Where \(\alpha\) is the learning rate at a given time, and (g) is the Gaussian function centered in a winner and with a neighborhood dispersion of \(h\). The decay function consists on simply multiplying the two given discounts, \(\gamma\), for the learning rate and the neighborhood distance.

\[ \alpha_{t+1} = \gamma_{\alpha} \cdot \alpha_{t} , \ \ h_{t+1} = \gamma_{h} \cdot h_{t} \]

This expression is indeed quite similar to that of Q-Learning, and the convergence is search in a similar fashion to this technique. Decaying the parameters can be useful in unsupervised learning tasks like the aforementioned ones. It is also similar to the functioning of the Learning Vector Quantization technique, also developed by Teuvo Kohonen.

Finally, to obtain the route from the SOM, it is only necessary to associate a city with its winner neuron, traverse the ring starting from any point and sort the cities by order of appearance of their winner neuron in the ring. If several cities map to the same neuron, it is because the order of traversing such cities have not been contemplated by the SOM (due to lack of relevance for the final distance or because of not enough precision). In that case, any possible ordered can be considered for such cities.

Implementing and testing the SOM

For the task, an implementation of the previously explained technique is provided in Python 3. It is able to parse and load any 2D instance problem modelled as a TSPLIB file and run the regression to obtain the shortest route. This format is chosen because for the testing and evaluation of the solution the problems in the National Traveling Salesman Problem instances offered by the University of Waterloo, which also provides the optimal value of the route of such instances and will allow us to check the quality of our solutions.

On a lower level, the numpy package was used for the computations, which enables vectorization of the computations and higher performance in the execution, as well as more expressive and concise code. pandas is used for loading the .tsp files to memory easily, and matplotlib is used to plot the graphical representation. These dependencies are all included in the Anaconda distribution of Python, or can be easily installed using pip .

To evaluate the implementation, we will use some instances provided by the aforementioned National Traveling Salesman Problem library. These instances are inspired in real countries and also include the optimal route for most of them, which is a key part of our evaluation. The evaluation strategy consists in running several instances of the problem and study some metrics:

• Execution time invested by the technique to find a solution.
• Quality of the solution, measured in function of the optimal route: a route that we say is “10% longer that the optimal route” is exactly 1.1 times the length of the optimal one.

The parameters used in the evaluation are the ones found by parametrization of the technique, by using the ones provided in previous works 2 as a starting point. These parameters are:

• A population size of 8 times the cities in the problem.
• An initial learning rate of 0.8, with a discount rate of 0.99997.
• An initial neighbourhood of the number of cities, decayed by 0.9997.

These parameters were applied to the following instances:

• Qatar , containing 194 cities with an optimal tour of 9352.
• Uruguay , containing 734 cities with an optimal tour of 79114.
• Finland , containing 10639 cities with an optimal tour of 520527.
• Italy , containing 16862 cities with an optimal tour of 557315.

The implementation also stops the execution if some of the variables decays under the useful threshold. An uniform way of running the algorithm is tested, although a finer grained parameters can be found for each instance. The following table gathers the evaluation results, with the average result of 5 executions in each of the instances.

The implementation yields great results: we are able to obtain sub-optimal solutions in barely 400 seconds of execution, returning acceptable results overall, with some remarkable cases like Uruguay, where we are able to find a route traversing 734 cities only 7.5% longer than the optimal in less than 25 seconds.

Final remarks

Although not thoroughly tested, this seems like an interesting application of the technique, which is able to lay some impressing results when applied to some sets of cities distributed more or less uniformly across the dimensions. The code is available in my GitHub and licensed under MIT, so feel free to tweak it and play as much as you wish with it. Finally, if you found have any doubts or inquires, do not hesitate to contact me. Also, I wanted to thank Leonard Kleinans for its help during our Erasmus in Norway, tuning the first version of the code.

Kohonen, T. (1998). The self-organizing map. Neurocomputing, 21(1), 1–6.  ↩︎

Brocki, L. (2010). Kohonen self-organizing map for the traveling salesperson. In Traveling Salesperson Problem, Recent Advances in Mechatronics (pp. 116–119)  ↩︎

Wolfram Demonstrations Project

Traveling salesman game.

• Open in Cloud
• Download to Desktop
• Copy Resource Object

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products .

Do not show again

Attention gamers! You are a traveling salesman. Your task: visit the cities (represented as dots on the gameboard) one by one by clicking them. Start anywhere you like. You will trace out a route as you proceed. You must visit every city once and then return to your starting point. The goal is to find the shortest possible route that accomplishes this. Your total distance is recorded at the bottom of the panel, along with the total distance of the best route that Mathematica can find.

Note that Mathematica will not always be able to find the best possible route, so it is conceivable that you will be able to find a shorter route than Mathematica 's best. While this is not likely, especially when there are only a small number of cities, if you play enough (and are skillful) you will eventually encounter this phenomenon.

Tips for game play: The scoreboard will reset when the number of cities is changed. The scoreboard is updated when the "new game" button is pushed after you have created a valid tour. You may undo an edge or clear your entire path without affecting your score. The radius slider can be used to find the closest city to your current location. Just crank it up until the red disk encounters its first dot, then slide it back. You may safely ignore this feature, although occasionally it can be quite useful (if you wish to pursue a "nearest neighbor" strategy, for instance). Serious gamers should hide both the distance tally and Mathematica 's best tour during play.

Contributed by: Bruce Torrence   (March 2011) Open content licensed under CC BY-NC-SA

Mathematica uses the FindShortestTour command to find its best tour.

An excellent resource for all things TSP is William Cook's site, www.tsp.gatech.edu .

Related Links

• FindShortestTour
• Traveling Salesman Problem
• Traveling Salesman Problem  ( Wolfram MathWorld )

Permanent Citation

Bruce Torrence "Traveling Salesman Game" http://demonstrations.wolfram.com/TravelingSalesmanGame/ Wolfram Demonstrations Project Published: March 7 2011

Share Demonstration

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Topics

• Combinatorics
• Optimization

Traveling Salesperson with Azure Quantum and Azure Maps

Learn how you can solve traveling salesperson challenges with given physical addresses and by taking traffic conditions into account.

The Traveling Salesperson Challenge

The traveling salesperson problem (also called the traveling salesman problem, abbreviated as TSP ) is a well-known problem in combinatorial optimization. Given a list of travel destinations and distances between each pair of destinations, it tries to find the shortest route visiting each destination exactly once and returning to the origin. The Azure Quantum optimization sample gallery contains a sample for solving this problem . There, you pass in a cost matrix (describing a generic “travel cost” between pairs of travel points) and get back an ordered list of destinations. Imagine, you could use physical addresses as input, consider traveling times (including current traffic conditions), and ultimately get driving directions for your optimized route as a result. Integrating Azure Maps into the solution makes this possible. Learn how to implement an API via Azure Functions , that ultimately takes physical addresses and returns an ordered list of these travel destinations representing the optimum travel route.

The Solution

The solution architecture contains a Function App making the functionality accessible via API, an Azure Maps account used to retrieve geo-information about travel destinations, and an Azure Quantum workspace (with an associated Azure Storage account) providing access to optimization solvers doing the actual route optimization. The architecture can be illustrated as follows:

Architecture of the overall solution

The whole solution is accessible as a public GitHub repository: hsirtl/traveling-salesperson-qio-maps .

TSP solutions often require you to pass in destinations via geo-coordinates and/or distances in miles/kilometers. It can be cumbersome to determine this information. Typically, you have a list of addresses and desire a web service to do the rest. This is exactly where Azure Maps comes into play. Azure Maps is a collection of geo-spatial services and SDKs that use fresh mapping data to provide geographic context to client applications. You can use a set APIs to work with addresses, places, and points of interest around the world, taking traffic flow into consideration and ultimately support visualization of data on maps.

For the TSP-solution, following Map services are relevant:

• Search Service - returning information to a given address (including latitude and longitude) via its GetSearchAddress -API.
• Route Service - returning information about distances between geo-locations via its GetRouteDirections -API.

Both these APIs used in sequence can be used to first get geo-locations to given addresses and then calculate a distance matrix containing distance information for each pair of destination points. The distance can either be expressed as physical distance (length in meters) or travel time (in seconds). In the sample solution on GitHub you’ll find all Azure Maps access methods in the mapsaccess.py -file.

Code for generating the cost matrix (distances between pairs of destination points).

Quantum Inspired Optimization (QIO) with Azure Quantum

Azure Quantum optimization solvers simulate certain quantum effects like tunneling on classical hardware. By exploiting some of the advantages of quantum computing on existing, classical hardware, they can provide a speedup over traditional approaches. For solving an optimization problem like TSP, you need to specify a cost function representing the quantity that you want to minimize (in our case: travel time or travel distance). So, you can summarize the challenge to be solved as follows:

• Quantity to be minimized: travel time or travel distance
• The salesperson can only be at one node at a time.
• The salesperson must be at a node at any given time.
• The salesperson must not visit a node a second time.
• All destination points must be visited at some point in time.
• The journey must start and end at one specific destination.

You’ll find the code for generating the cost function in the travelingsalesperson.py -file. It is derived from the traveling-salesperson-sample my esteemed colleague Frances Tibble created. So, lots of Kudos to Frances!

A serverless API via Azure Functions

The easiest way to make the overall solution accessible to non-quantum developers is via an API. Azure Functions have some tempting qualities that make them an ideal tool for this purpose:

• They are serverless, so you don’t need to worry about underlying infrastructure.
• The programming model is simple, so you can focus on the core functionality (calling Azure Maps and then Azure Quantum).
• Functions can be called via (authenticated) http-requests.

You’ll find the main implementation code for the function in the __init__.py -file. These are the most relevant lines of code calling Azure Maps and Azure Quantum for solving the TSP for a given set of travel destinations.

Function code calling Azure Maps and Azure Quantum to solve the TSP for a set of destinations.

Deployment of the solution

With several Azure services involved, a manual setup via the Azure portal would be too error-prone. The sample solution is equipped with an Azure Resource Manager (ARM) template representing ‘Infrastructure as Code’, i.e. a deployable specification of all Azure resources needed. The ARM template has following specifications:

• appName - used as a prefix for Azure resource names
• location - datacenter regions the services should be deployed to
• Azure Storage Account - needed by the Azure Quantum Workspace
• Azure Quantum Workspace - providing access to optimization solvers
• Azure Maps Account - geo-spacial services needed
• Azure Function App - access point (API) for the functionality

A GitHub action executes the deployment. Its specification is stored in the CD-Full-Deployment.yml -file. If you fork the solution repository to your GitHub account, make sure to create a service principal with Contributor-rights on your Azure subscription and configure two Actions secrets:

• AZURE_CREDENTIALS with the output generated during the service principal creation.
• AZURE_SUBSCRIPTION with the Azure subscription ID.

After that, you can run the action (e.g., manually by using the workflow_dispatch event trigger ), which executes following steps:

• Log into Azure (using the AZURE_CREDENTIALS ).
• Create the resource group (its name specified via the AZURE_RESOURCE_GROUP_NAME -environment variable).
• Deploy the infrastructure (specified in the azuredeploy.json ARM template).
• Setup the Python environment
• Install the Function App
• Configure the credentials needed by the Azure Quantum workspace (specified in the azuredeploy.rbac.json ) ARM template.

Solving Traveling Salesperson Challenges

After the GitHub workflow has successfully completed the setup, you can call the Function-API providing a list of addresses. You can call the Function via following URL:

URL you TSP-API is accessible under (APP_NAME specified in the GitHub action)

Make sure you provide that information in the body of the request. A sample workload could look as follows (containing the addresses of all Microsoft regional offices in Germany).

Request body to be passed via the Azure Function call.

After a few seconds, the function should return an ordered list of these destinations representing the optimal route. The result also provides the overall cost (travel distance or travel time) of that route. A sample output looks as follows:

Response containing an ordered list of destinations and travel cost.

Azure Quantum is a great cloud quantum computing service, with a diverse set of quantum solutions and technologies. Its optimization solvers provide a speedup over traditional approaches in many optimization challenges, one of which is the Traveling Salesperson problem. Azure Maps can complement an optimization solution by providing geo-information to physical addresses, which is needed by existing optimization algorithms. By packaging the logic into Azure Functions, it is accessible via a Web-API. In this post, I showed you how, by utilizing these cloud services, you can solve traveling salesperson challenges with given physical addresses and by taking traffic conditions into account.

Azure Quantum Stuff

Quantum blogs.

• Graph Theory

Travelling Salesman in a Grid

The travelling salesman has a map containing m*n squares. He starts from the top left corner and visits every cell exactly once and returns to his initial position (top left). The time taken for the salesman to move from a square to its neighbor might not be the same. Two squares are considered adjacent if they share a common edge and the time taken to reach square b from square a and vice-versa are the same. Can you figure out the shortest time in which the salesman can visit every cell and get back to his initial position?

Input Format

The first line of the input is 2 integers m and n separated by a single space. m and n are the number of rows and columns of the map. Then m lines follow, each of which contains (n – 1) space separated integers. The j th integer of the i th line is the travel time from position (i,j) to (i,j+1) (index starts from 1.) Then (m-1) lines follow, each of which contains n space integers. The j th integer of the i th line is the travel time from position (i,j) to (i + 1, j).

Constraints

1 ≤ m, n ≤ 10 Times are non-negative integers no larger than 10000.

Output Format

Just an integer contains the minimal time to complete his task. Print 0 if its not possible to visit each cell exactly once.

Sample Input

Sample Output

Explanation

As its a 2*2 square, all cells are visited. 5 + 7 + 8 + 6 = 26

Cookie support is required to access HackerRank

Seems like cookies are disabled on this browser, please enable them to open this website

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Dynamic Programming or DP
• What is memoization? A Complete tutorial
• Dynamic Programming (DP) Tutorial with Problems
• Tabulation vs Memoization
• Optimal Substructure Property in Dynamic Programming | DP-2
• Overlapping Subproblems Property in Dynamic Programming | DP-1
• Steps for how to solve a Dynamic Programming Problem

Advanced Topics

• Bitmasking and Dynamic Programming | Set 1 (Count ways to assign unique cap to every person)
• Digit DP | Introduction
• Sum over Subsets | Dynamic Programming

Easy problems in Dynamic programming

• Count all combinations of coins to make a given value sum (Coin Change II)
• Subset Sum Problem
• Introduction and Dynamic Programming solution to compute nCr%p
• Cutting a Rod | DP-13
• Painting Fence Algorithm
• Longest Common Subsequence (LCS)
• Longest Increasing Subsequence (LIS)
• Longest subsequence such that difference between adjacents is one
• Maximum size square sub-matrix with all 1s
• Min Cost Path | DP-6
• Longest Common Substring (Space optimized DP solution)
• Count ways to reach the nth stair using step 1, 2 or 3
• Count Unique Paths in matrix
• Unique paths in a Grid with Obstacles

Medium problems on Dynamic programming

• 0/1 Knapsack Problem
• Printing Items in 0/1 Knapsack
• Unbounded Knapsack (Repetition of items allowed)
• Egg Dropping Puzzle | DP-11
• Word Break Problem | DP-32
• Vertex Cover Problem (Dynamic Programming Solution for Tree)
• Tile Stacking Problem
• Box Stacking Problem | DP-22
• Partition problem | DP-18

Travelling Salesman Problem using Dynamic Programming

• Longest Palindromic Subsequence (LPS)
• Longest Common Increasing Subsequence (LCS + LIS)
• Find all distinct subset (or subsequence) sums of an array
• Weighted Job Scheduling
• Count Derangements (Permutation such that no element appears in its original position)
• Minimum insertions to form a palindrome | DP-28
• Ways to arrange Balls such that adjacent balls are of different types

Hard problems on Dynamic programming

• Palindrome Partitioning
• Word Wrap Problem
• The Painter's Partition Problem
• Program for Bridge and Torch problem
• Matrix Chain Multiplication | DP-8
• Printing brackets in Matrix Chain Multiplication Problem
• Maximum sum rectangle in a 2D matrix | DP-27
• Maximum profit by buying and selling a share at most k times
• Minimum cost to sort strings using reversal operations of different costs
• Count of AP (Arithmetic Progression) Subsequences in an array
• Introduction to Dynamic Programming on Trees
• Maximum height of Tree when any Node can be considered as Root
• Longest repeating and non-overlapping substring
• Top 20 Dynamic Programming Interview Questions

Travelling Salesman Problem (TSP):  

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle. 

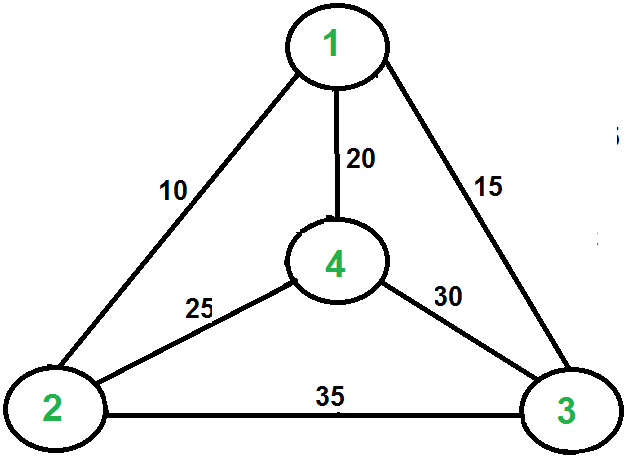
For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem. 

Naive Solution:  

1) Consider city 1 as the starting and ending point.

2) Generate all (n-1)! Permutations of cities. 

3) Calculate the cost of every permutation and keep track of the minimum cost permutation. 

4) Return the permutation with minimum cost. 

Time Complexity: ?(n!) 

Dynamic Programming:  

Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex I (other than 1), we find the minimum cost path with 1 as the starting point, I as the ending point, and all vertices appearing exactly once. Let the cost of this path cost (i), and the cost of the corresponding Cycle would cost (i) + dist(i, 1) where dist(i, 1) is the distance from I to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far. 

Now the question is how to get cost(i)? To calculate the cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems. 

Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i . We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on. Note that 1 must be present in every subset.

Below is the dynamic programming solution for the problem using top down recursive+memoized approach:-

For maintaining the subsets we can use the bitmasks to represent the remaining nodes in our subset. Since bits are faster to operate and there are only few nodes in graph, bitmasks is better to use.

For example: –  

10100 represents node 2 and node 4 are left in set to be processed

010010 represents node 1 and 4 are left in subset.

NOTE:- ignore the 0th bit since our graph is 1-based

Time Complexity : O(n 2 *2 n ) where O(n* 2 n) are maximum number of unique subproblems/states and O(n) for transition (through for loop as in code) in every states.

Auxiliary Space: O(n*2 n ), where n is number of Nodes/Cities here.

For a set of size n, we consider n-2 subsets each of size n-1 such that all subsets don’t have nth in them. Using the above recurrence relation, we can write a dynamic programming-based solution. There are at most O(n*2 n ) subproblems, and each one takes linear time to solve. The total running time is therefore O(n 2 *2 n ). The time complexity is much less than O(n!) but still exponential. The space required is also exponential. So this approach is also infeasible even for a slightly higher number of vertices. We will soon be discussing approximate algorithms for the traveling salesman problem.

Next Article: Traveling Salesman Problem | Set 2  

References:  

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf  

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf  

Please Login to comment...

Similar reads.

• Dynamic Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications

Using Self-Organizing Maps for Travelling Salesman Problem

diego-vicente/ntnu-som

Folders and files, repository files navigation, self-organizing maps for travelling salesman problem, introduction.

Self-organizing maps (SOM) or Kohonen maps are a type of artificial neural network (ANN) that mixes in an interesting way the concepts of competitive and cooperative neural networks. A SOM behaves as a typical competitive ANN, where the neurons fight for a case. The interesting twist added by Kohonen is that when a neurons wins a case, the prize is shared with its neighbors . Typically, the neighborhood is bigger at the beginning of the training, and it shrinks in order to let the system converge to a solution.

Applying SOM to TSP

One of the most interesting applications of this technique is applying it to the Travelling Salesman Problem , in which we can use a coordinate map and trace a route using the neurons in the ANN. By defining weight vectors as positions in the map, we can iterate the cities and treat each one as a case that can be won by a single neuron. The neuron that wins the case gets it weight vector updated to be closer to the city, but also its neighbors get updated. The neurons are placed in a 2D space, but they are only aware of a single dimension in their internal ANN, so their behavior is like an elastic ring that will eventually fit all the cities in the shortest distance possible.

The method will rarely find the optimal route among the cities, and it is quite sensitive to changing the parameters, but it usually lays more than acceptable results taking into account the time consumed.

In the repository you can find the source code to execute it (in Python 3) as well as the necessary maps in the assets/ folder (already trimmed to be used in the code). The maps used have been extracted from the TSP page in University of Waterloo . There is also a diagrams/ folder that contains all the execution snapshots that had to be included in the report (present as well as a .tex file).

The code present in this repository was delivered as Project 3 in the IT3105 Artificial Intelligence Programming course in the Norwegian University of Science and Technology the course 2016-2017. The code was developed by Leonard Kleinhans and Diego Vicente . The code is licensed under MIT License.

• Python 50.3%

Distilling Privileged Information for Dubins Traveling Salesman Problems with Neighborhoods

This paper presents a novel learning approach for Dubins Traveling Salesman Problems(DTSP) with Neighborhood (DTSPN) to quickly produce a tour of a non-holonomic vehicle passing through neighborhoods of given task points. The method involves two learning phases: initially, a model-free reinforcement learning approach leverages privileged information to distill knowledge from expert trajectories generated by the LinKernighan heuristic (LKH) algorithm. Subsequently, a supervised learning phase trains an adaptation network to solve problems independently of privileged information. Before the first learning phase, a parameter initialization technique using the demonstration data was also devised to enhance training efficiency. The proposed learning method produces a solution about 50 times faster than LKH and substantially outperforms other imitation learning and RL with demonstration schemes, most of which fail to sense all the task points.

1 Introduction

Motion planning with kinematic constraints should be considered in real-world vehicular applications such as mobile robots and fixed-wing aerial vehicles. Moreover, pathfinding to the points of interest should consider the sensors’ specifications on the vehicles. The vanilla TSP, however, does not account for non-holonomic constraints or sensor specifications. To address this issue, one of the specific variations of TSP called the Dubins TSP with neighborhoods (DTSPN) has been studied. DTSPN differs from the vanilla TSP in two key ways. First, the vehicle moves at a constant speed with angular velocity as its control input while following Dubins kinematics. Second, if the target points are within the sensor range of the vehicle, they are automatically marked as "visited". Therefore, the vehicle does not have to go directly to the points of interest.

A standard approach to solve DTSPN is to generate sample visiting points around the task points to construct an Asymmetric TSP (ATSP) visiting those sample points [ 17 ] so that algorithms for ATSP (e.g., branch-and-cut [ 38 ] , Lin-Kernighan heuristic (LKH) [ 12 , 6 ] ) can be utilized. However, the complexity of this procedure grows with the number of sample visiting points; thus, it has a limitation in producing tours in a real-time manner.

On the other hand, learning-based methods have recently been widely studied as they can quickly generate solution path points for TSP in the form of heuristic solvers. Some research has been conducted to solve the TSP problem using the attention model, focusing on scenarios with up to 100 nodes [ 19 , 18 ] . Such transformer models have many parameters to learn due to their complex structure, requiring significant memory and leading to extended training times. These limitations become more evident when applied to the DTSPN, which considers the sensor radius and kinematics of the vehicle. Furthermore, conventional neural networks [ 45 , 3 ] , and transformer [ 19 , 4 ] consider only points of interest, while the agent needs to pass neighborhoods of the points in DTSPN. Also, it is very challenging to train with model-free learning due to the large state-action space. The agent should explore and find a better solution with model-free RL, but it could be difficult to train if the solution space is much smaller than the state-action space. In brief, conventional learning for TSP and model-free learning cannot solve DTSPN.

In our early guess, imitation learning could be a breakthrough to overcome the challenges. We designed imitation learning with expert data from the existing method [ 6 ] . Behavioral Cloning (BC) and Generative Adversarial Imitation Learning (GAIL) train agents using expert trajectories, which consist of the expert’s states and actions, especially when the reward function is unknown. However, BC can easily lose generalization, and GAIL also has difficulties training both a discriminator and an actor network. To overcome exploration, Hindsight Experience Replay (HER) [ 1 ] is suggested. HER was effective in the sparse reward problem but was not much researched on many goal problems such as [ 2 ] including the DTSP. RL with demonstrations is an emerging method to train online using expert data or policy. Deep Q-Learning (DQfD) [ 13 ] and DDPG from Demonstrations (DDPGfD) [ 44 ] initialize the model with expert demonstrations offline and train the model with model-free RL. Jump-Start with Reinforcement Learning (JSRL) [ 41 ] uses an expert policy in the initial episode and follows a more learning policy when the agent achieves better.

Inspired by the distilling of privileged information research [ 16 , 26 ] , we propose an algorithm called Distilling Privileged information for Dubins Traveling Salesman Problems (DiPDTSP). In DiPDTSP, we distill the knowledge acquired by experts into an adaptation network that doesn’t use privileged information. So, the agent can understand the environments from the expert’s perspective, where only the locations of tasks are given. We performed several steps to distill the expert’s knowledge. First, we collect the expert’s state and action sets from the existing heuristic methods [ 6 ] and train the policy and value networks to initialize. The expert’s trajectories are also used as a criterion for the reward function that guides the agent to sense all task points. Since the hand-crafted reward function might not be well-designed, imitation learning that learns reward function directly from expert trajectories is adopted as our baseline model.

Considering these challenges, this paper presents the following three main contributions:

We propose a new learning approach to address the DTSPN by combining two methods: Distilling PI and RL with demonstrations.

Accordingly, we promote efficient exploration by initializing the policy and value networks via behavioral cloning using expert trajectories and privileged information.

The proposed algorithm computes the DTSPN path about 50 times faster than the heuristic method using only the given positions of tasks and agents.

2 Related Works

2.1 dubins tsp with neighborhoods.

DTSPN was solved using exact methods and heuristic methods. Traditional transformation methods use the strategy for converting DTSPN into ATSP to apply the exact method [ 17 ] . It shows that the DTSPN problem makes ATSP with the number of nodes multiplied by the number of samples for each node. Intersecting neighborhood concepts are introduced that can transform DTSPN into Generalized TSP (GTSP) [ 28 ] . After transforming DTSPN into ATSP, LKH3 [ 12 ] and exact method [ 38 ] are applied to solve ATSP. Finally, LKH3 generates the TSP path of each drone and they follow their own path with respect to Dubins vehicle kinematics.

2.2 Combining demonstrations with Reinforcement Learning

Previous research has effectively integrated reinforcement learning with demonstrations, accelerating the learning process for tasks ranging from the cart-pole swing-up task [ 35 ] to more complex challenges like humanoid movements [ 30 ] and dexterous manipulation [ 31 ] . These studies initialize policy search methods with policies trained via behavioral cloning or model-based methods.

Recent advancements have further expanded the use of demonstrations in RL, with developments in deep RL algorithms like DQN [ 25 ] and DDPG [ 22 ] . For instance, DQfD [ 13 ] refines a Q-function by implementing a margin loss, ensuring that expert actions are assigned higher Q values than other actions.DDPGfD [ 44 ] tackles simple robotic tasks, like peg insertion, by incorporating demonstrations into DDPG’s replay buffer. Additionally, the DDPG approach was combined with HER [ 1 ] to solve complicated multi-step tasks [ 27 ] . The Demo Augmented Policy Gradient (DAPG) [ 31 ] approach integrates demonstrations into the policy gradient method by augmenting the RL loss function. The DeepMimic [ 29 ] approach combines demonstrations into reinforcement learning by incorporating imitation terms in the reward function. Moreover, JSRL, one of our baselines combined with PPO, utilizes a guided policy that provides a curriculum of starting states resulting in efficient exploration [ 41 ] .

Existing studies have focused on integrating demonstrations through established RL methods, such as initializing policies, modifying the loss function, shaping rewards, and utilizing replay buffers. Our research extends this domain by adhering to foundational strategies and applying the Learning Using Privileged Information (LUPI) technique. This approach enables us to extract more nuanced information from demonstrations, thereby presenting a novel method for integrating demonstrations with RL.

2.3 Learning using Privileged Information

Learning using privileged information (LUPI) frameworks [ 42 , 43 ] is a noticeable strategy to enhance the performance of various tasks ranging from image classification to machine translation, effectively managing uncertainty [ 20 , 16 ] . LUPI leverages privileged information that is only available during the training stage. Privileged information is used to bridge the gap between training and testing conditions. DiPCAN proposes a pedestrian collision avoidance model only using a first-person FOV by reconstructing the privileged pedestrian position [ 26 ] . Meanwhile, several works use expert trajectories for dynamic models [ 10 , 40 ] and combine RL and LUPI [ 5 , 21 , 37 ] . Unlike the related works we’ve mentioned, our work doesn’t require an additional teacher’s policy network, and student policy directly accesses the expert’s trajectory. However, it is only available at the first stage of training, not the whole process.

Similarly, knowledge distillation trains a compact student model to mimic the behavior of a larger teacher model, transferring its expertise within resource-constrained settings [ 14 , 24 ] . It is primarily used for model compression; recently, it has proliferated in computer vision area [ 46 , 47 , 11 , 23 , 9 ] . Distilling policy networks in deep reinforcement learning [ 33 ] ensures rapid, robust learning through entropy regularization [ 8 ] . Distillation accelerates learning in the multi-task learning domain [ 34 , 39 ] . The robustness of distilling is highlighted by [ 2 , 7 ] . Our distillation model has the encoder and the adaptation network. The adaptation network will mimic the encoder’s output vector even if the PI is not given.

3.1 Dubins Kinematics with Deep RL

Note that the kinematics Eq 2 - 4 are not changed whether the state includes expert information. The goal of the MDP problem is to minimize the goal time while the goal is sensing all the tasks. The d i subscript 𝑑 𝑖 d_{i} italic_d start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT is initially deactivated or zero, and when the T i subscript 𝑇 𝑖 T_{i} italic_T start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT is sensed, d i subscript 𝑑 𝑖 d_{i} italic_d start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT is activated and set to 1. The agent is assumed to move with constant velocity by Dubins kinematics. The actions are discretized into 7 between [-0.6 π 𝜋 \pi italic_π , 0.6 π 𝜋 \pi italic_π ] rad/s with a turning radius of 30m.

Without experts’ trajectories, designing rewards that effectively guide an agent’s task-sensing order becomes a significant challenge. Whether the rewards are sparse or dense, based on the proximity to the nearest task, deriving a DTSP path is difficult. However, leveraging expert trajectories simplifies the problem and facilitates more straightforward model training. In this problem, the original goal is to sense all the tasks in the short path, but we can change it into following an expert path that senses all the tasks reasonably. Consequently, the reward function should be designed to encourage the agent to adhere to this expert path. This problem has not yet been widely researched, so the reward function needs to be newly designed for this paper. We design the reward function consisting of two terms: imitation rewards R I superscript 𝑅 𝐼 R^{I} italic_R start_POSTSUPERSCRIPT italic_I end_POSTSUPERSCRIPT and task rewards R G superscript 𝑅 𝐺 R^{G} italic_R start_POSTSUPERSCRIPT italic_G end_POSTSUPERSCRIPT as follows.

Here, r 𝑟 r italic_r is the relative distance between the expert path and the current agent’s position. The agent gets R I superscript 𝑅 𝐼 R^{I} italic_R start_POSTSUPERSCRIPT italic_I end_POSTSUPERSCRIPT rewards to guide the agent to follow the expert path and penalize if the agent gets far from the expert path. If the agent is over 6m away from the expert path, it gets negative rewards based on the distance. The task rewards R G superscript 𝑅 𝐺 R^{G} italic_R start_POSTSUPERSCRIPT italic_G end_POSTSUPERSCRIPT encourage the agent to sense all the tasks. The agent gets a reward for each step of the exploration. When the vehicle finds the tasks that have not been found (i.e. at the moment d i subscript 𝑑 𝑖 d_{i} italic_d start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT is activated), the agent gets five for each task. The episode terminates when the agent senses all the tasks or is over 60m away from the expert path in the training phase. But we terminate only when all the tasks are sensed or the time step reaches 300 to test performance with baselines.

3.2 Pretraining with Behavioral Cloning

While model-free RL often shows generalization performance than model-based learning, it can be intractable when the search space is much larger than the solution space. To deal with the intractability, we initialize the policy and value network using learning from the expert’s trajectories. The bunch of the expert’s trajectories is called the demonstrations. We collect 5000 demonstrations with the same initial points, but the random positions of the tasks using [ 6 ] . The derived paths are used to calculate action inversely. The greedy controller chooses one of the discretized actions that closely find the next path point for each step. The datasets containing expert state, action, and reward train the initial actor network in a behavioral cloning manner. By following the expert trajectories, the expected Q-value can also be calculated so that the critic network is initialized by minimizing MSE loss between model outputs and the Q-value of expert datasets. The expected Q-value can also be calculated along the expert trajectories with designed reward functions. The critic network is initialized by minimizing MSE loss between model outputs and the Q-value of expert datasets.

3.3 Phase 1: RL Fine-tuning with Privileged Information

Even though the model was initialized with BC, BC does not guarantee the policy’s effectiveness due to the distributional shift between expert states and the policy’s state. After the model is initialized with behavioral cloning, the training phase consists of two procedures: RL fine-tuning with privileged information from the experts and PI-free policy adaptation to solve DTSPN without an expert. In phase 1 of Fig. 2, The model-free PPO networks consist of an encoder and a policy network(so as a critic). Encoder gets the common state s 𝑠 s italic_s and privileged information p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT . The encoder derives the latent variable z 𝑧 z italic_z ; the policy and critic network get common state s 𝑠 s italic_s and the latent variable z 𝑧 z italic_z and derive action and Q-value, respectively. The initialized encoders and actor-critic networks are trained in a model-free PPO manner. We generate one thousand new problems and expert paths and observe performance and convergence.

3.4 Phase 2: PI-free Policy Adaptation

Returning to the original problem, the agent should sense all the tasks without access to expert data, including the order of tasks. To do that, the agent should replicate the action from phase 1 regardless of the availability of privileged information p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT . Given that the input state differs from that used in phase 1, a distinct network, “adaptation” in Fig. 2 should be introduced that gets only common states s 𝑠 s italic_s and derives latent variable z ′ superscript 𝑧 ′ z^{\prime} italic_z start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT . The adaptation network should imitate the encoder network to make the same action when combining the policy network. The adaptation network is trained to derive z ′ superscript 𝑧 ′ z^{\prime} italic_z start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT in the direction of minimizing mean squared error(MSE), ‖ z − z ′ ‖ 2 superscript norm 𝑧 superscript 𝑧 ′ 2 ||z-z^{\prime}||^{2} | | italic_z - italic_z start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT | | start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT . The policy network got the same input as model-free RL. For phase 2, supervised learning, we use the same 5,000 episodes when initializing PPO networks and encoders. After the phase 2 training, The agent can calculate action with given positions of task and agent, and without privileged information, p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT , by learning that given situations are identical regardless of the existence of p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT .

4 Experiments

4.1 experiment setup.

We collected state, action, and reward tuples from 5,000 episodes, organizing these into mini-batches of 512 for processing. The actor network was initialized using an Adam optimizer with a learning rate of 0.001 and optimized using a cross-entropy loss function. Throughout 1,000 epochs, we monitored the training process to ensure convergence, achieving a validation accuracy of 92% for the behavior cloning policy.

Subsequently, we trained the PPO model while freezing the actor network, allowing the agent to follow the expert policy over 3 million steps. This process involved collecting experiences to calculate the Q-value using our designed dense reward function, which incorporates a discount factor of γ = 0.95 𝛾 0.95 \gamma=0.95 italic_γ = 0.95 . During this phase, only the critic network was trained to minimize the Mean Squared Error (MSE) loss. In the final stage, we trained the PPO model for an additional 3 million steps, updating both the actor and critic networks using the PPO loss function. Adam optimizers were employed for both networks, with learning rates set at 0.003 for the actor and 0.001 for the critic, respectively. The initialization of the networks, model-free RL, and supervised RL takes about 3 hours each with an i7-8700CPU and NVIDIA GTX 1060 graphics card.

We evaluate the proposed model in the environment shown in Fig. 1 . The map size is 800m x 800m. The agent starts from a specific point on the map, aligning its heading angle with that of the expert path’s initial point. Tasks within this environment are uniformly distributed across the map’s domain. The vehicle is equipped with a sensing radius of 58 meters. We tested a few baselines and conducted ablation studies of DiPDSTP.

4.2 Baselines

Exploration is the main challenge of learning how to generate a DTSP path. In previous research, HER was used to overcome exploration difficulties [ 1 ] . HER is known to perform well in the sparse reward setting rather than dense rewards. Although many baselines used HER, it is commonly used with an off-policy algorithm, so PPO, which we used to train with model-free RL, is not applicable. Therefore, the additional off-policy algorithms DQN and SAC are implemented to combine with HER. Also, to use the sparse reward, we only give a reward of 1 and -1 when the agent senses the task each time and the time step exceeds the maximum time steps respectively. We compare our DiPDTSP to the following baselines.

4.2.1 BC [ 32 ]

We train π θ subscript 𝜋 𝜃 \pi_{\theta} italic_π start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT policy from the expert’s trajectory using supervised learning. We treat the expert’s demonstrations as state-action pairs ( s , a ∗ ) 𝑠 superscript 𝑎 (s,a^{*}) ( italic_s , italic_a start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) , and minimize the Cross-Entropy loss function L ⁢ ( a ∗ , π θ ⁢ ( s ) ) 𝐿 superscript 𝑎 subscript 𝜋 𝜃 𝑠 L(a^{*},\pi_{\theta}(s)) italic_L ( italic_a start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_π start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT ( italic_s ) )

4.2.2 GAIL [ 15 ]

subscript 𝐸 𝜏 𝑙 𝑜 𝑔 𝐷 𝑠 𝑎 subscript 𝐸 𝜏 𝑙 𝑜 𝑔 1 𝐷 𝑠 𝑎 E_{\tau}(log(D(s,a)))+E_{{\tau}}(log(1-D(s,a))) italic_E start_POSTSUBSCRIPT italic_τ end_POSTSUBSCRIPT ( italic_l italic_o italic_g ( italic_D ( italic_s , italic_a ) ) ) + italic_E start_POSTSUBSCRIPT italic_τ end_POSTSUBSCRIPT ( italic_l italic_o italic_g ( 1 - italic_D ( italic_s , italic_a ) ) ) . D 𝐷 D italic_D is an indicator that tells whether the behavior policy is equal to the expert’s policy. It follows the TRPO rule with cost l ⁢ o ⁢ g ⁢ ( D ) 𝑙 𝑜 𝑔 𝐷 log(D) italic_l italic_o italic_g ( italic_D ) .

4.2.3 PPO [ 36 ] with dense rewards

We train π θ subscript 𝜋 𝜃 \pi_{\theta} italic_π start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT policy using only common states s 𝑠 s italic_s and our designed reward function in Section ( 5 ) 5 ( 5 ) by Proximal Policy Optimization, a single-step on-policy model-free algorithm. In other words, it only trains to follow the expert path with guided rewards without distilling the PI process.

4.2.4 PPO with frozen policy network

In Phase 1 of our training method, we trained both the encoder and policy networks. However, we attempted to train only the encoder network for the ablation study while freezing the subsequent network components and remaining other processes the same. These components were initially trained with BC initialization, allowing for RL fine-tuning with fewer variables.

4.2.5 PPO with JSRL [ 41 ]

We train π θ subscript 𝜋 𝜃 \pi_{\theta} italic_π start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT policy using only common states s 𝑠 s italic_s and the sparse reward function in Section ( 5 ) 5 ( 5 ) by PPO, a single-step on-policy model-free algorithm. In the initial process, the agent follows the expert policy with [ 6 ] while it achieves most of the goals, then the agent tries to explore with learning policy to sense a few of remained goals. If the agent satisfies the predefined achievement or average success rate, the part of following expert policy is reduced, and the exploring or exploiting with learning policy increases.

4.2.6 DQfD [ 13 ] + HER

In the single Q network, DQN is trained with demonstrations with sparse rewards and online. The full demonstrations are initially stacked in the replay buffer and utilized to initialize the Q-network. Then, it starts to train online, and the offline demonstrations are covered with online experience. In total, it uses a mixture of offline and online data and full online data at last.

4.2.7 Overcoming exploration in RL with demonstrations [ 27 ]

It originally utilized DDPG, Q-filter, HER, and JSRL. We replaced DDPG with SAC to accommodate discrete actions. During training, the loss function maximizes cumulative reward while minimizing the BC loss between actions from the learning model and experts. We label this method as "SAC(overcome)" for simplicity.

4.3 Evaluation Metrics

To compare the performance of DiPDTSP with other baseline methods in Sec. 4.2 , we define several evaluation metrics.

4.3.1 Average reward and return

Our objective functions in RL, average reward and discounted return, represent how the agent closely follows the expert and senses the tasks. We tested our method and baselines using the dense reward in Sec. 3.1 . The higher reward and return represent that the agent follows the expert trajectories closely.

4.3.2 Sensing rate

The sensing rate indicates the average number of visited tasks out of 20. Because of rigorous termination conditions, the agent cannot sense all task points within a single episode. The sensing rate reflects the agent’s performance straightforwardly.

The time metric indicates the running time of the algorithms with successful episodes. If none of the episodes succeed, we exclude the evaluation of the method with this metric. We compare DiPDTSP and other baseline methods with the above evaluation metrics. The baselines are also trained with the same data in the same total timesteps as DiPDTSP.

4.4 Simulation Results

Table. 1 presents the results obtained from the proposed method, DiPDTSP, along with the baseline methods. Across all the baseline methods, they exhibit a common challenge of failing to sense 20 tasks in each episode. Most episodes terminate within 30 steps when employing imitation learning methods (Sec. 4.2.1 , 4.2.2 ), while expert trajectory lengths typically span 150 to 300 steps. In comparison, the performance of imitation learning methods falls short of that achieved by PPO. The PPO model outperforms imitation learning methods, but its training speed is slow due to the large exploration space. The imitation learning methods struggle to solve DTSPN primarily due to challenges with distributional shifts and generalization difficulties. The agent only succeeds in sensing a few tasks. The agent gets far from the expert trajectories due to the compounding errors. The results suggest that imitation learning approaches may struggle to match the expert performance in challenging scenarios like the one presented in this multi-goal problem.

We experimented with various versions of PPO, the original with dense reward, jump start, and training-only encoder network. Dense reward with PPO succeeds better than imitation learning and HER method due to the intuitively guided reward function. However, it is not enough to succeed in achieving all goals. A process similar to ours involves freezing the subsequent network after the encoder during the first training phase (Sec. 4.2.4 ). This approach shows effective results in that the agent can perfectly sense all the tasks in some episodes. Still, the results show that more training variables need to be tuned.

Also, using SAC and DQfD with HER with a sparse reward design shows worse performance than simple PPO with dense rewards. An agent in SAC suffers from exploring and sensing many goals perfectly during episodes. DQfD initially trains the expert demonstrations offline, but it is challenging to train with sparse rewards. This result shows that training for varying episodes and multi-goal problems is difficult, although the HER is known to be effective in training sparse reward problems.

The jump-start method is the method to overcome challenging exploration, it shows the effective performance of training that seems to follow the expert policy in the training process. JSRL and SAC(overcome) use BC initialization as ours. However, BC with and without privileged information p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT makes a large performance difference. We monitored the validation accuracy during BC initialization with 1,000 fixed pairs of training datasets. We checked that the validation accuracy of the training state with p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT is 92%, 59% otherwise without p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT . So our method uses BC initialization with p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT train with better-initialized models than JSRL and SAC(overcome). We can infer that p e subscript 𝑝 𝑒 p_{e} italic_p start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT is a critical feature influencing BC performance as well as the model-free RL performance.

We apply three skills in DiPDTSP: (i)initializing networks and getting skills from experts by behavioral cloning, (ii) increasing generalizability using model-free learning and PI, and (iii) supervised learning to make the agent sense all task points without PI. While other methods fail to recover when they choose undesired actions, the agent with DiPDTSP is more robust to deviations from the expert’s trajectories. DiPDTSP can almost perfectly follow the expert path and sense all the tasks in all episodes shown in Table. 1 and Fig. 4 . The average reward, return, and optimality of DiPDTSP are slightly lower than the expert but very close to the expert performance. The proposed algorithm can generate a DTSPN path in less than 1 second, which is approximately 57 times faster than the heuristic method which takes about 39 seconds.

5 Conclusions

We have presented a learning framework that generates a DTSPN path using only the positions of the agent and the task points. The overall structure combines schemes for distilling PI and RL with demonstrations. Learning with privileged information enhances the learning performance of BC to initialize networks and model-free RL. The distilling process makes the model generate the same actions whether the agent has privileged information. The simulation results show that our work outperforms the existing imitation learning and RL with demonstration methods in sensing all task points. Our method closely follows the expert performance while taking more than 50x less computation time than the heuristic solver.

This work was supported by Unmanned Vehicles Core Technology Research and Development Program through the National Research Foundation of Korea (NRF), Unmanned Vehicle Advanced Research Center (UVARC) funded by the Ministry of Science and ICT (MSIT), the Republic of Korea (#2020M3C1C1A0108237512). Also, the fourth author acknowledges financial supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by MSIT (#2019-0-00075, Artificial Intelligence Graduate School Program(KAIST)).

• Andrychowicz et al. [2017] M. Andrychowicz, F. Wolski, A. Ray, J. Schneider, R. Fong, P. Welinder, B. McGrew, J. Tobin, O. Pieter Abbeel, and W. Zaremba. Hindsight experience replay. Advances in neural information processing systems , 30, 2017.
• Arora et al. [2018] H. Arora, R. Kumar, J. Krone, and C. Li. Multi-task learning for continuous control. arXiv preprint arXiv:1802.01034 , 2018.
• Bello et al. [2016] I. Bello, H. Pham, Q. V. Le, M. Norouzi, and S. Bengio. Neural combinatorial optimization with reinforcement learning. arXiv preprint arXiv:1611.09940 , 2016.
• Bresson and Laurent [2021] X. Bresson and T. Laurent. The transformer network for the traveling salesman problem. arXiv preprint arXiv:2103.03012 , 2021.
• Chen et al. [2020] D. Chen, B. Zhou, V. Koltun, and P. Krähenbühl. Learning by cheating. In Conference on Robot Learning , pages 66–75. PMLR, 2020.
• Cho et al. [2018] D.-H. Cho, D.-S. Jang, and H.-L. Choi. Heterogeneous, multiple depot multi-uav path planning for remote sensing tasks. In 2018 AIAA Information Systems-AIAA Infotech@ Aerospace , page 0894. 2018.
• Czarnecki et al. [2018] W. Czarnecki, S. Jayakumar, M. Jaderberg, L. Hasenclever, Y. W. Teh, N. Heess, S. Osindero, and R. Pascanu. Mix & match agent curricula for reinforcement learning. In International Conference on Machine Learning , pages 1087–1095. PMLR, 2018.
• Czarnecki et al. [2019] W. M. Czarnecki, R. Pascanu, S. Osindero, S. Jayakumar, G. Swirszcz, and M. Jaderberg. Distilling policy distillation. In The 22nd international conference on artificial intelligence and statistics , pages 1331–1340. PMLR, 2019.
• Do et al. [2019] T. Do, T.-T. Do, H. Tran, E. Tjiputra, and Q. D. Tran. Compact trilinear interaction for visual question answering. In Proceedings of the IEEE/CVF International Conference on Computer Vision , pages 392–401, 2019.
• Elia et al. [2020] K. Elia, L. Antonio, R. René, M. Matthias, K. Vladlen, and S. Davide. Deep drone acrobatics. RSS: Robotics, Science, and Systems , 2020.
• Garcia et al. [2018] N. C. Garcia, P. Morerio, and V. Murino. Modality distillation with multiple stream networks for action recognition. In Proceedings of the European Conference on Computer Vision (ECCV) , pages 103–118, 2018.
• Helsgaun [2000] K. Helsgaun. An effective implementation of the lin–kernighan traveling salesman heuristic. European journal of operational research , 126(1):106–130, 2000.
• Hester et al. [2018] T. Hester, M. Vecerik, O. Pietquin, M. Lanctot, T. Schaul, B. Piot, D. Horgan, J. Quan, A. Sendonaris, I. Osband, et al. Deep q-learning from demonstrations. In Proceedings of the AAAI conference on artificial intelligence , volume 32, 2018.
• Hinton et al. [2015] G. Hinton, O. Vinyals, and J. Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531 , 2015.
• Ho and Ermon [2016] J. Ho and S. Ermon. Generative adversarial imitation learning. Advances in neural information processing systems , 29, 2016.
• Huang et al. [2021] X. Huang, H. Deng, W. Zhang, R. Song, and Y. Li. Towards multi-modal perception-based navigation: A deep reinforcement learning method. IEEE Robotics and Automation Letters , 6(3):4986–4993, 2021.
• Isaacs and Hespanha [2013] J. T. Isaacs and J. P. Hespanha. Dubins traveling salesman problem with neighborhoods: A graph-based approach. Algorithms , 6(1):84–99, 2013.
• Kool et al. [2018] W. Kool, H. Van Hoof, and M. Welling. Attention, learn to solve routing problems! arXiv preprint arXiv:1803.08475 , 2018.
• Kwon et al. [2020] Y.-D. Kwon, J. Choo, B. Kim, I. Yoon, Y. Gwon, and S. Min. Pomo: Policy optimization with multiple optima for reinforcement learning. Advances in Neural Information Processing Systems , 33:21188–21198, 2020.
• Lambert et al. [2018] J. Lambert, O. Sener, and S. Savarese. Deep learning under privileged information using heteroscedastic dropout. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , pages 8886–8895, 2018.
• Lee et al. [2020] J. Lee, J. Hwangbo, L. Wellhausen, V. Koltun, and M. Hutter. Learning quadrupedal locomotion over challenging terrain. Science robotics , 5(47):eabc5986, 2020.
• Lillicrap et al. [2015] T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, and D. Wierstra. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971 , 2015.
• Liu et al. [2019] Y. Liu, K. Chen, C. Liu, Z. Qin, Z. Luo, and J. Wang. Structured knowledge distillation for semantic segmentation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition , pages 2604–2613, 2019.
• Lopez-Paz et al. [2015] D. Lopez-Paz, L. Bottou, B. Schölkopf, and V. Vapnik. Unifying distillation and privileged information. arXiv preprint arXiv:1511.03643 , 2015.
• Mnih et al. [2013] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller. Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602 , 2013.
• Monaci et al. [2022] G. Monaci, M. Aractingi, and T. Silander. Dipcan: Distilling privileged information for crowd-aware navigation. Robotics: Science and Systems (RSS) XVIII , 2022.
• Nair et al. [2018] A. Nair, B. McGrew, M. Andrychowicz, W. Zaremba, and P. Abbeel. Overcoming exploration in reinforcement learning with demonstrations. In 2018 IEEE international conference on robotics and automation (ICRA) , pages 6292–6299. IEEE, 2018.
• Obermeyer et al. [2012] K. J. Obermeyer, P. Oberlin, and S. Darbha. Sampling-based path planning for a visual reconnaissance unmanned air vehicle. Journal of Guidance, Control, and Dynamics , 35(2):619–631, 2012.
• Peng et al. [2018] X. B. Peng, P. Abbeel, S. Levine, and M. Van de Panne. Deepmimic: Example-guided deep reinforcement learning of physics-based character skills. ACM Transactions On Graphics (TOG) , 37(4):1–14, 2018.
• Peters and Schaal [2008] J. Peters and S. Schaal. Reinforcement learning of motor skills with policy gradients. Neural networks , 21(4):682–697, 2008.
• Rajeswaran et al. [2017] A. Rajeswaran, V. Kumar, A. Gupta, G. Vezzani, J. Schulman, E. Todorov, and S. Levine. Learning complex dexterous manipulation with deep reinforcement learning and demonstrations. arXiv preprint arXiv:1709.10087 , 2017.
• Ross and Bagnell [2010] S. Ross and D. Bagnell. Efficient reductions for imitation learning. In Proceedings of the thirteenth international conference on artificial intelligence and statistics , pages 661–668. JMLR Workshop and Conference Proceedings, 2010.
• Rusu et al. [2015] A. A. Rusu, S. G. Colmenarejo, C. Gulcehre, G. Desjardins, J. Kirkpatrick, R. Pascanu, V. Mnih, K. Kavukcuoglu, and R. Hadsell. Policy distillation. arXiv preprint arXiv:1511.06295 , 2015.
• Rusu et al. [2016] A. A. Rusu, N. C. Rabinowitz, G. Desjardins, H. Soyer, J. Kirkpatrick, K. Kavukcuoglu, R. Pascanu, and R. Hadsell. Progressive neural networks. arXiv preprint arXiv:1606.04671 , 2016.
• Schaal [1996] S. Schaal. Learning from demonstration. Advances in neural information processing systems , 9, 1996.
• Schulman et al. [2017] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347 , 2017.
• Sorokin et al. [2022] M. Sorokin, J. Tan, C. K. Liu, and S. Ha. Learning to navigate sidewalks in outdoor environments. IEEE Robotics and Automation Letters , 7(2):3906–3913, 2022.
• Sundar and Rathinam [2017] K. Sundar and S. Rathinam. Algorithms for heterogeneous, multiple depot, multiple unmanned vehicle path planning problems. Journal of Intelligent & Robotic Systems , 88:513–526, 2017.
• Teh et al. [2017] Y. Teh, V. Bapst, W. M. Czarnecki, J. Quan, J. Kirkpatrick, R. Hadsell, N. Heess, and R. Pascanu. Distral: Robust multitask reinforcement learning. Advances in neural information processing systems , 30, 2017.
• Tolani et al. [2021] V. Tolani, S. Bansal, A. Faust, and C. Tomlin. Visual navigation among humans with optimal control as a supervisor. IEEE Robotics and Automation Letters , 6(2):2288–2295, 2021.
• Uchendu et al. [2023] I. Uchendu, T. Xiao, Y. Lu, B. Zhu, M. Yan, J. Simon, M. Bennice, C. Fu, C. Ma, J. Jiao, et al. Jump-start reinforcement learning. In International Conference on Machine Learning , pages 34556–34583. PMLR, 2023.
• Vapnik and Vashist [2009] V. Vapnik and A. Vashist. A new learning paradigm: Learning using privileged information. Neural networks , 22(5-6):544–557, 2009.
• Vapnik et al. [2015] V. Vapnik, R. Izmailov, et al. Learning using privileged information: similarity control and knowledge transfer. J. Mach. Learn. Res. , 16(1):2023–2049, 2015.
• Vecerik et al. [2017] M. Vecerik, T. Hester, J. Scholz, F. Wang, O. Pietquin, B. Piot, N. Heess, T. Rothörl, T. Lampe, and M. Riedmiller. Leveraging demonstrations for deep reinforcement learning on robotics problems with sparse rewards. arXiv preprint arXiv:1707.08817 , 2017.
• Vinyals et al. [2015] O. Vinyals, M. Fortunato, and N. Jaitly. Pointer networks. Advances in neural information processing systems , 28, 2015.
• Wang et al. [2018] X. Wang, R. Zhang, Y. Sun, and J. Qi. Kdgan: Knowledge distillation with generative adversarial networks. Advances in neural information processing systems , 31, 2018.
• Wang et al. [2019] X. Wang, R. Zhang, Y. Sun, and J. Qi. Adversarial distillation for learning with privileged provisions. IEEE transactions on pattern analysis and machine intelligence , 43(3):786–797, 2019.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 24 April 2024

Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems

• Jia Si   ORCID: orcid.org/0000-0003-0737-4905 1 , 2 ,
• Shuhan Yang 1 ,
• Yunuo Cen 1 ,
• Jiaer Chen 1 ,
• Yingna Huang 1 ,
• Zhaoyang Yao 1 ,
• Dong-Jun Kim 1 ,
• Kaiming Cai 1 ,
• Jerald Yoo   ORCID: orcid.org/0000-0002-3150-1727 1 ,
• Xuanyao Fong   ORCID: orcid.org/0000-0001-5939-7389 1 &
• Hyunsoo Yang   ORCID: orcid.org/0000-0003-0907-2898 1  

Nature Communications volume  15 , Article number:  3457 ( 2024 ) Cite this article

1217 Accesses

3 Altmetric

Metrics details

• Electrical and electronic engineering
• Magnetic devices

The growth of artificial intelligence leads to a computational burden in solving non-deterministic polynomial-time (NP)-hard problems. The Ising computer, which aims to solve NP-hard problems faces challenges such as high power consumption and limited scalability. Here, we experimentally present an Ising annealing computer based on 80 superparamagnetic tunnel junctions (SMTJs) with all-to-all connections, which solves a 70-city traveling salesman problem (TSP, 4761-node Ising problem). By taking advantage of the intrinsic randomness of SMTJs, implementing global annealing scheme, and using efficient algorithm, our SMTJ-based Ising annealer outperforms other Ising schemes in terms of power consumption and energy efficiency. Additionally, our approach provides a promising way to solve complex problems with limited hardware resources. Moreover, we propose a cross-bar array architecture for scalable integration using conventional magnetic random-access memories. Our results demonstrate that the SMTJ-based Ising computer with high energy efficiency, speed, and scalability is a strong candidate for future unconventional computing schemes.

Similar content being viewed by others

Local environment in biomolecular condensates modulates enzymatic activity across length scales

Giant nanomechanical energy storage capacity in twisted single-walled carbon nanotube ropes

Scaling deep learning for materials discovery

Introduction.

The demands for future data-intensive and energy-efficient computing tasks overwhelm the computational power of conventional von Neumann architectures 1 . For example, NP-hard problems are often encountered in combinatorial optimizations 2 , resource allocation 3 , cryptography 4 , finance 5 , image processing 6 , tour planning 7 , and job sequencing 8 , and their computational time and hardware resources increase exponentially with the problem size, which makes them very difficult or impossible to be solved by conventional computers in a finite time. These problems can be mapped to the Ising model, a mathematical model to characterize interactions between magnetic spins 9 . The dynamics of the model is algorithm- based, i.e. by constructing a proper coupling matrix and allowing the system to evolve utilizing an intrinsic convergence property of the Ising model, the ground state could be obtained as a solution to the corresponding problems. However, as the system might be trapped in many local minima, the annealing process has usually been adopted in Ising computers to address such limitations. It is commonly agreed that adding fluctuations prevents the Ising computer from being stuck at the local minima.

Efficient algorithms and hardware systems for finding an optimal or near-optimal solution of an Ising model at a fast speed and low power have been sought. Adiabatic quantum computing (AQC) 10 , 11 and quantum computing 12 , 13 , 14 , 15 based on superconducting qubits are capable of converging the Ising model by tunneling out of local minima to the global minima. A 100-node Maxcut problem was solved using a quantum computer of 2048 spins with huge power consumption 16 . Besides the high cost and complexity of cryogenic temperature, this proof-of-concept system was limited by the sparse connections only between the nearest neighbors, which leads to sub-optimal outcomes 17 . Simulated annealing based on CMOS implementations was exploited for parallel Ising computing, including central processing units (CPU) 18 , 19 , graphics processing units (GPU) 20 , and field-programmable gate array (FPGA) 21 , 22 . These hardware have reported as large as 16,384 spins, however, it requires huge hardware resources for generating random numbers to introduce stochasticity to escape from the local minima 4 , 18 , 23 , 24 . Coherent Ising machine (CIM) is an optical scheme with competitive energy efficiency. However, it requires a long fiber ring cavity and relies on external FPGA for implementing coupling 25 , 26 . The temporal multiplexing process is also time-consuming and hard to expand to large systems. Recently, experiments and simulation works have investigated various devices to emulate the behavior of Ising spins by taking advantage of their intrinsic physics. An 8-spin asynchronous probabilistic computer based on superparamagnetic tunnel junctions for solving integer factorization tasks of values up to 945 was demonstrated 4 . SPICE simulations of 16-city TSP using simulated annealing method were presented 27 . Other works such as 8-spin phase-transition nano-oscillators 28 , multiferroic oxide devices with a high thermal stability 29 , and magnetoresistive random access memory (MRAM) 30 , 31 have also conceptually proved that spin-based devices are suitable for representing Ising units. However, these works have encountered challenges in either partially-connected Ising spins or small scalability which limit the Ising computer from solving practical problems.

TSP discussed in this paper is a well-known problem which is much beyond the limitation of locally connected Ising models. Other combinatorial optimization problems, such as knapsack problems, coloring problems, and number partitioning, need all-to-all connection to satisfy specific constraints 9 . In practice, an additional graph embedding process is often required when mapping to 2-dimensional CMOS circuitry which only considered the coupling between adjacent spins 32 , 33 , 34 . Since the embedding increases the required number of auxiliary spins and causes spin connections to change, the annealing accuracy is degraded significantly, especially when the problem size is large. This means that supporting a fully connected Ising model is highly recommended for dealing with a wide range of problems. Another problem is the rapidly increasing connectivity when considering large-scale systems, which usually results in huge energy consumption and latency. Since the number of spins that a particular annealing processor can handle limit the scale of the problem that can be solved, how to solve complex problems with limited hardware in an energy-efficient way has also drawn significant attention.

In this work, we experimentally report a scalable Ising computer based on 80 SMTJs with all-to-all connections and successfully solve the 4761-node TSP problem. The intrinsic stochasticity in SMTJ enables ultra-fast and low-power Ising annealing without using extra resources for random number generation and Metropolis determining process 7 . By combining global annealing with intrinsic annealing in SMTJ, the convergence of the Ising problem is guaranteed especially in large-scale Ising problems. The method to determine parameters of global annealing is discussed. With an all-to-all connection among Ising spins, the combinatorial optimization of 9-city TSP is solved with the optimal solution. We further develop the algorithm for constrained TSP (CTSP) with no extra auxiliary Ising bits both in algorithm and hardware, indicating the superiority and flexibility of this Ising computer. Furthermore, we propose an optimization strategy based on graph partitioning (GP) and CTSP and experimentally solved a 70-city TSP, which typically needs 4761 nodes, on our 80-node Ising computer with a near-optimal solution. The system can obtain the lowest power consumption of 0.64 mW as well as high energy efficiency of 39 solutions per second per watt among state-of-art Ising annealers. We have experimentally demonstrated that large-scale Ising problems can be solved by small-scale hardware in an energy-efficient way.

SMTJ-based artificial Ising spin

Various NP-hard problems can be solved by constructing corresponding Ising models and observing the ground states during evolution processes. Figure  1a shows an all-to-all connected Ising model, whose Ising Hamiltonian can be written as

where \(H\) is the total energy of the system, \(N\) is the total number of spins, \({s}_{i}\) is the \(\,i\) -th spin with one of two states; “+1” (Ising spin up) or “−1” (Ising spin down), \({J}_{i,j}\) is the coefficient of coupling between the \(i\) -th and the \(j\) -th spins, and \({h}_{i}\) is the external field of the \(\,i\) -th spin. For a fixed configuration of other spins than \({s}_{k}\) , the probability of \({s}_{k}\) staying in the down-state is given by

where \(\Lambda=\frac{\partial H}{\partial {s}_{k}}\) (see Supplementary Note  1 ).

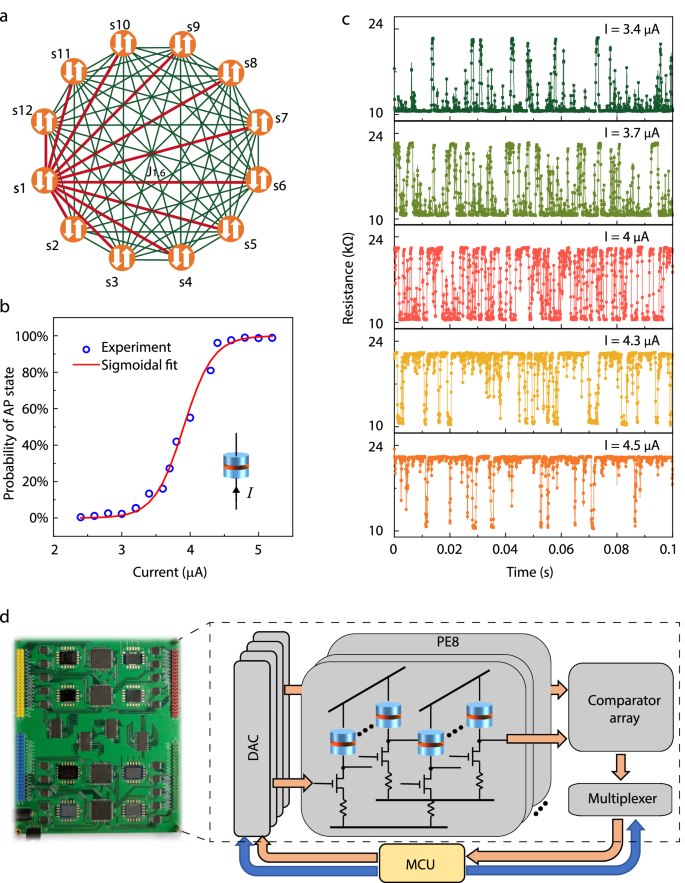
a All-to-all connected 12-spin Ising model with s represents the spin and J 1,6 represents the coupling between s1 and s6. b Sigmoidal fit of probability of AP state ( \({p}_{{AP}}\) ) of an SMTJ under different input currents ( I ). \({p}_{{{{{{\rm{AP}}}}}}}=\frac{1}{1+{e}^{-4.672\times (I-3.905{{{{{\rm{\mu }}}}}}{{{{{\rm{A}}}}}})}}\) . Inset: diagram of an SMTJ. A tunneling barrier layer is sandwiched by a reference layer and a free layer. c Time-dependent resistance of an SMTJ under different input currents ( I ). d Photograph and schematic diagram of SMTJ-based Ising computer. The system contains 8 processing elements (PEs), 4 digital-to-analog converters (DACs), a comparator array, a multiplexer and a microcontroller unit (MCU). Each PE has 10 SMTJ computing units. Each computing unit includes a transistor and a resistor to adjust the property into stochastic. Blue lines and orange arrows represent the control and data flow, respectively.

One natural implementation of this Ising spin is based on a stochastic nanomagnet. The inset of Fig.  1b shows the sketch of an SMTJ, consisting of a tunneling barrier sandwiched by a reference layer and a free layer (see Methods section). Because of the small device diameter (~50 nm), the energy barrier of the free layer between the anti-parallel (AP) and parallel (P) states is low that the retention time of either state is in the range of μs to ms, similar to previous studies 4 , 35 . The SMTJ resistance, measured as a function of time in Fig.  1c , shows preferred AP states at high currents and P states at low currents. When the current ( I ) is ~4 μA, SMTJ shows an equal chance of AP and P states. The probability of the AP state under different input currents over 0.1 s is fitted in Fig.  1b by a sigmoid function:

where \({{{{{\rm{a}}}}}}=4.67 \, {{{{{\rm{and\; b}}}}}}=3.9 \, {{{{{\rm{\mu }}}}}}{{{{{\rm{A}}}}}}.\) In order to emulate Ising spin \({s}_{k}\) with our SMTJ device, we only need to make the probability of the down-state of \({s}_{k}\) to be equal to that for the AP state of SMTJ, namely \({p}{\_}{{{{{{\rm{\_}}}}}}{{{{{\rm{AP}}}}}}}={p}{\_}{{{{{{\rm{\_}}}}}}\downarrow }\) , with two calibration coefficients. Thus, we can derive the form of the current \({{I\_}}_{k}\) injected to SMTJ as (see Supplementary Note  1 ):

where \(c=1/{kT}\) is the effective inverse temperature which can be conducted for global annealing.

Intrinsic annealing in SMTJs-based Ising computer

By integrating 80 SMTJs with a peripheral circuit and a microcontroller unit (MCU), we build an 80-node Ising computer (see Supplementary Note  2 ). Each Ising spin in Eq. ( 1 ) is emulated by an SMTJ with intrinsic randomness, where P (AP) state represents spin-up (down). Figure  1d shows the photograph of the printed circuit board (PCB) and the diagram of the system (see Methods section). The system contains 8 processing elements (PEs); each PE has 10 SMTJ computing units. Each SMTJ computing unit includes a transistor and a resistor to adjust the state of SMTJ into stochastic. During the computing process, an MCU examines the states of all SMTJs by reading the output of comparator arrays through multiplexers and generates new input voltages for digital-to-analog converters (DACs) according to the updating rule in Eq. ( 4 ) (see Supplementary Note  3 for calibration of 80 SMTJ computing units).

During the evolution process, an Ising solver could be easily trapped in a local minimum state. To avoid this non-optimal solution, annealing algorithms such as simulated annealing (SA) or quantum annealing (QA) were developed. The general idea of SA is to make the system evolve from a high temperature to a low temperature gradually 7 . The convergence and relaxation of SA can be mathematically provable 36 . During each iteration, a random number is generated for stochasticity and introduced to determine whether the result in this iteration should be accepted or not. In QA, quantum fluctuations cause quantum tunneling between states 17 . In both SA and QA, stochasticity needs to be introduced into the annealing process. In contrast, our Ising system utilizes the intrinsic stochastic behaviors of SMTJ to perform the Metropolis process of standard SA in hardware, which greatly saves the solution time and hardware resources for generating randomness (see Supplementary Note  4 ). Besides, our Ising computer has an all-to-all connection which has wider application scenarios, as well as a better capability of escaping from local minima.

Ising mapping of N-city TSP and CTSP

We have applied our Ising computer to the TSP problem, one of the combinatorial optimization problems, which applies to various sectors, such as vehicle routing, logistics, planning, and scheduling. The goal is to find the shortest route that visits all listed cities once and only once given distances between the cities in the list. In order to solve this problem, we first map N -city-TSP to an \({N}^{2}\) -spin Ising model, or \({(N-1)}^{2}\) -spin model assuming a fixed starting city. Figure  2a shows the coordinates of 9 cities and Fig.  2b shows the 81-spin Ising model, whose rows indicate the cities and columns indicate the visiting order. We define the binary spin, s , as \({s}_{i,j}\)  = 1 if city i is visited as j -th city or \({s}_{i,j}\)  = −1 otherwise. The total Hamiltonian of TSP is expressed by 9

where the first term is a constraint that represents only one city is visited at the j -th visit, and the second term represents one city is visited only one time. \(w\) is a constant small enough ( \(0 \, < \, w \, < \, 1\) ) not to violate the two constraints of the TSP cycle. \({d}_{i,{i{{\hbox{'}}}}}\) is the distance between city \(i\) and city \({i{{\hbox{'}}}}\) . According to Eqs. ( 1 ) and ( 5 ), coupling matrix \(J\) of 81 spins could be obtained, as shown in Fig.  2c (see Supplementary Note  5 ). It shows that spins in the same row or column have strong coupling, as indicated by the first two terms in Eq. ( 5 ).

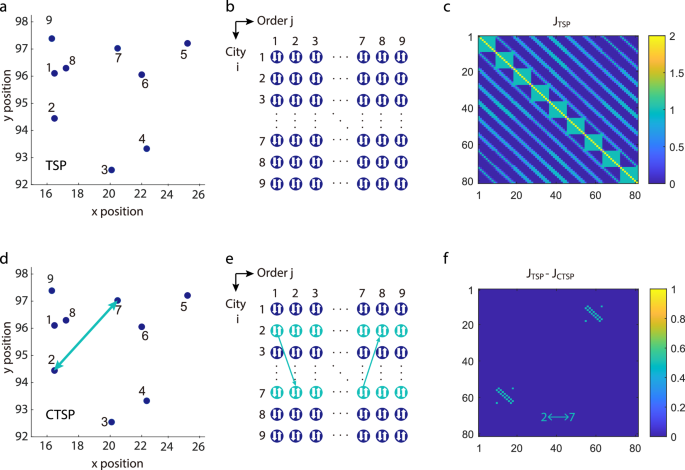
a Coordinates of all 9 cities used in this problem which are the first 9 cities in the dataset Burma14 from TSPLIB. b Ising spin representation for 9-city TSP (81 spins). Rows indicate names of cities and columns indicate the visiting order. Each spin can be 1 (visited) or −1 (not visited) in each iteration. c Color map of the coupling matrix J TSP of 9-city TSP, and the color bar represents an effective energy with the unit of kT . Here, k is the Boltzmann constant and T is the temperature. d Constrained TSP (CTSP) with a fixed vising sequence from city 2 to city 7 or from city 7 to city 2. The arrows represent the visiting sequence. e The Ising spin representation for CTSP with the fixed visiting sequence in d . Arrows represent possible vising sequences. f Color map of the difference of coupling matrix between TSP (J TSP ) in a and CTSP (J CTSP ) in d . Arrows represent the fixed vising sequences from city 2 to city 7 or from city 7 to 2.

We define CTSP as the visiting orders of some cities are enforced during the traveling. This is quite useful in real-life scenarios. For example, a delivery man collects food and drinks at shop A and must deliver hot drinks to B first even though the total cost is higher than optimal. We propose an algorithm for solving CTSP by adding negative “distance” to the Hamiltonian. For example, suppose that city A and city B are required to be connected in the CTSP as city 2 and city 7 shown in Fig.  2d , and then we add the term

such that the energy of a path, where city A and city B are connected, is always lowered by \(\theta .\) When \(\theta\) is sufficiently large, the optimal path must have city 2 and city 7 connected. Thus, the total Hamiltonian of the CTSP is expressed by

Constructing an Ising model for CTSP is exactly the same as TSP except for extra allowed visiting sequences, as shown in Fig.  2e . This would lead to a modification of the coupling matrix of \(J\) according to Eq. ( 7 ) (see the deduction of \({J}_{{CTSP}}\) in Supplementary Note  6 ). From Fig.  2f we can clearly see the differences between \({J}_{{CTSP}}\) and \({J}_{{TSP}}\) . This algorithm of CTSP fits for arbitrary constraints of visiting sequences as well as their combinations.

Experimental demonstration of 9-city TSP

We first run a 9-city TSP in the 80 SMTJ-based Ising computer at a relatively low but non-zero effective temperature to examine the intrinsic annealing in SMTJ. The iteration time is set comparable to the longest retention time of SMTJs to avoid reading previous spin states. In our experiments, we set the iteration time as 0.1 ms. As shown in Fig.  3a , as the effective inverse temperature ( c ) is increased quickly to 0.5, the system converges rapidly to a low energy state within 50 iterations and reaches the ground state after 4000 iterations. It should be noted that the intrinsic stochasticity in SMTJs helps the system escape from local minima without an extra annealing process, as shown in the right inset of Fig.  3a . Figure  3b illustrates the evolution of 9 spins out of 81 spins. The evolution of all 81 spins can be found in Supplementary Note  7 .

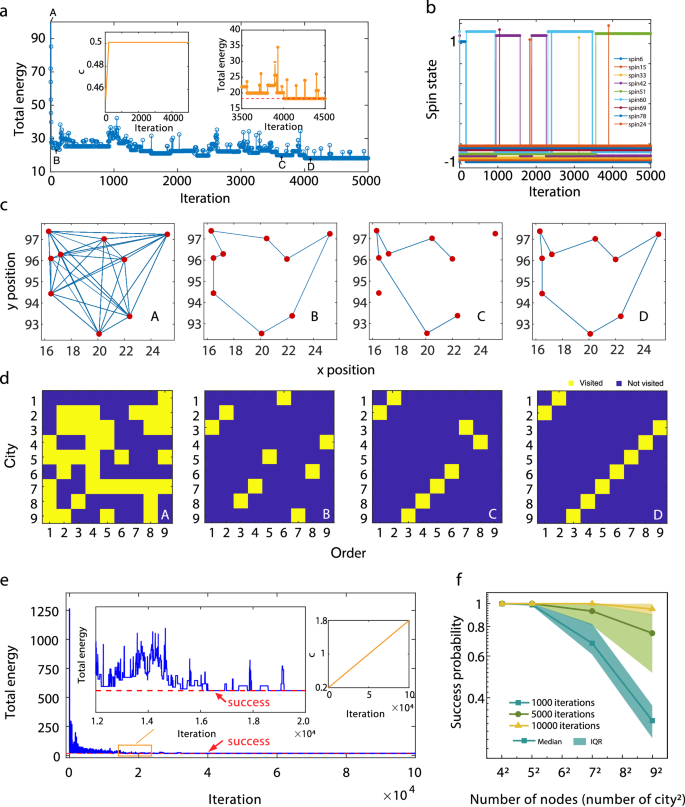
a Total energy transition of 9-city TSP with 5000 iterations (the optimal solution with the energy of 18.23 corresponds to the dashed horizontal line). Insets: effective inverse temperature ( c ) and total energy within 3500–4500 iterations. b Evolution of 9 representative SMTJ states in 5000 iterations. An offset is used in the y -axis to show each SMTJ clearly. c Visiting routes of state A, B, C, and D in a . d Corresponding Ising spins of state A, B, C, and D in a . The yellow squares represent ‘visited ( \({s}_{i,j}=1\) )’ and the purple squares represent ‘not visited ( \({s}_{i,j}=-1\) )’. e Total energy transition with increasing c from 0.2 to 1.8. Left inset: zoom-in view of total energy transition with increasing c from 0.392 to 0.52. Right inset: transition of c with iterations. The red dashed line represents the optimal path (success). f Success probability of solving TSP with varying the node size. The data points and shadows represent the median value and the interquartile range (IQR), respectively.

We choose four states in Fig.  3a to inspect the traveling path in Fig.  3c and their Ising spins, namely \({s}_{i,j}\) , as shown in Fig.  3d . The yellow square in Fig.  3d represents \({s}_{i,j}=1\) (visited) and the blue square represents \({s}_{i,j}=-1\) (not visited). In an initial state A, the spin states are randomly set and then converge to a relatively low energy at state B. State C is an intermediate solution during the annealing process. State D is the optimal solution satisfying two constraints of the TSP. Because we anneal the system to a relatively low but non-zero temperature so that the convergence to a sub-optimal state could be guaranteed, and at the same time, the intrinsic randomness in SMTJ helps the system to escape from local minima and find a ground state quickly. We test 10 different random initial states each with 5000 iterations and find that in all cases the system can obtain a relatively small energy, as shown in Supplementary Note  8 . However, there is a probability that the system jumps out of the ground state because of the non-zero temperature. If we continue to observe the evolution in a large timescale, the system would move back to the global minimum state. In some cases, where the speed and near-optimal solution matter but the accurate optimal solution is not, the number of iterations can be chosen to be small.

Further global annealing of the system to a lower effective temperature may guarantee the convergence of the computation. Here we use linear annealing as an example to examine the convergence of this algorithm in a very large-iteration limit. The initial temperature should be chosen sufficiently high to ensure that the thermal energy exceeds any energy barrier ( \(\Delta H{=H}_{\max }-{H}_{\min }\) ) within the system, while still adhering to the fundamental constraints of the specific Ising model. For a given N-city TSP, \({H}_{\max }\) in Eq. ( 5 ) can be estimated as \(w\times N\times \bar{d}\) , assuming that the distance between any two cities is the same as the average distance \(\bar{d}\) . Similarly, \({H}_{\min }\) can be estimated as \(w\times N\times {d}_{\min }\) . Therefore, the initial \(c\) of 9-city TSP in our experiment can be estimated as \({c}_{{{{{{\rm{initial}}}}}}}\, \sim 1/\Delta H=0.07\) , where \(w=0.5\) , \(N=9\) for a total of 9 cities, \(\bar{d}=4\) and \({d}_{\min }=0.8\) for the average and shortest distance of each two cities, respectively in Fig.  3c . We then choose \({c}_{{{{{{\rm{initial}}}}}}}\)  = 0.2 which is sufficiently safe for annealing. As the temperature linearly decreases, the dynamical system gradually stabilizes. The final temperature should be low enough i.e., \({c}_{{{{{{\rm{final}}}}}}} \, \gg \, 1/\Delta H\) , to freeze all possible fluctuations. Here we set \({c}_{{{{{{\rm{final}}}}}}}=1.8\) which is at least one order larger than \(1/\Delta H\) . This can also be verified by observing randomly generated states under \({c}_{{{{{{\rm{final}}}}}}}\) for long iterations. Regarding the annealing speed, if several changes in the spin configuration are observed under each value of c , then this annealing speed is valid. Plenty trials are required to find the proper annealing speed (details in Supplementary Note  8 ).

In Fig.  3e we can find the first global minimum energy appears after 16,500 iterations, and converge to the ground state after 40,000 iterations. Temperature schedules can be optimized to reduce iteration numbers, e.g. increase the effective temperature in the first few time steps, and then decrease gradually, or learned by the reinforcement learning method 37 . In practice, we use one memory to store the minimum energy state during the computation, and another memory to record the final energy state. We take the minimum value of these two results as the solution. Figure  3f shows the success probability (defined as finding the optimal path) of TSP with various node sizes. The success probability of 9-city TSP reaches 95% after 10 4 iterations. The success probability with the parameter \(w\) in Eq. ( 5 ) which determines the relative strength of the constrain term and distance term is also discussed. If the \(w\) is too large, then the probabilities of violations, namely the invalid path, would increase, as shown in Supplementary Note  8 . If \(w\) is too small, then the effect of the distance term is small, which results in a slower convergence to the ground state.

The advantages of this annealer are threefold: (1) Selective working modes by using different temperature schemes. One is the probabilistic sampling mode working at a constant temperature, which is similar to an asynchronous probabilistic computer 4 ; the other is the annealing mode conducted by reducing the effective temperature. (2) Fast speed and low power consumption to find the ground state because of the intrinsic annealing properties in SMTJ. (3) Global annealing outperforms probabilistic sampling in achieving efficient convergence, especially for large-scale problems.

We have implemented a synchronous design with a lower requirement on the speed of peripheral circuits. This design also effectively mitigates issues such as leakage, sneak currents, and parasitic resistances which might encountered in asynchronous hardware with a memristive (or resistive) crossbar array.

Compressing 70-city TSP to 80-node Ising computer

Generally, the number of spins required for an N -city TSP is ( N -1) 2 , which limits the scalability of TSP on state-of-the-art computing systems. Here, we propose a graph Ising compressing algorithm based on CTSP that can significantly reduce the number of spins and interactions for solving a TSP. Figure  4a is an example of how we apply this algorithm to our 80-node SMTJ Ising computer for solving a 70-city TSP (4761 nodes, st70 data set from TSPLIB 38 ). The major steps of this algorithm can be described as follows: (a) divide the cities into several smaller groups until the number of cities in each group is less than 10 by GP method; (b) solve TSP within each group separately; (c) integrate neighboring groups to obtain an initial path of the whole group; and (d) optimize the path in (c) by a CTSP window sliding over the whole map.

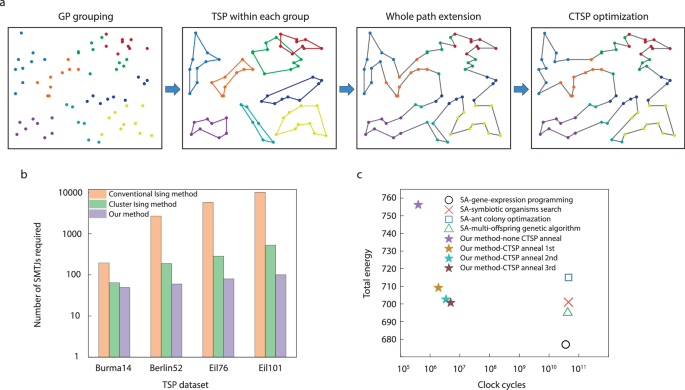
a Optimization algorithm for 70-city TSP. b Number of required SMTJs for various problems using different methods. Burma14, berlin52, eil76, and eil101 are TSP of 14, 52, 76, and 101 cities, respectively. c Comparison of total Ising energy (path) and total clock cycles for final solution with different SA-based algorithms, including symbiotic organisms search 40 , ant colony optimazation 41 , multi-offspring genetic algorithm 42 , and gene-expression programming 7 . Our method is tested on our Ising system and others are tested on Intel Core-i7 PC. In this comparison, our system runs at a main frequency of 10 kHz.

It is worth mentioning that GP is also an Ising problem. When converting a global TSP into local TSPs, using GP would be more hardware-friendly for our Ising computer compared to other clustering algorithms. It is based on the idea that the original graph can be separated into multiple sub-graphs depending on the Euclidean distance. The number of spins required for solving GP is ~ N and thus, GP is quite efficient for local TSPs since the problem size can be reduced to ~ \({\left(N-1\right)}^{2}/a\) , where \(a\) is the number of groups, and each TSP can be optimized independently (see GP mapping in Supplementary Note  9 ).

The final step (d) is based on CTSP, where a rectangular window slides over the path and cuts it into several disconnected lines, among which the two longest lines are chosen and the edge cities are connected as a circular path (Supplementary Note  10 ). The CTSP is solved within each window for sub-area optimization without changing the visiting order of edge cities. After this, the two lines at the edge cities are opened and CTSP is carried out again after sliding to the next window. GP-CTSP-based optimization algorithm provides an efficient way of finding near-optimal solutions for large-scale TSP on limited hardware resources.

Figure  4b shows the comparison of numbers of spins for different TSPs by a conventional Ising method 9 , cluster Ising method 39 , and our method. The required number of spins in our method is relatively unchanged for various TSPs, while that of other methods increases substantially with the scale of the problem. Figure  4c shows the total path of 70-city TSP as a function of iteration number using different SA-based algorithms, including symbiotic organisms search 40 , ant colony optimization 41 , multi-offspring genetic algorithm 42 , and gene-expression programming 7 . Finally, we obtain the near-optimal path with a total energy of 700.71, which is slightly higher than the optimal solution of 675. However, the iteration number for an optimized solution is 4.9 \(\times\) 10 6 by our method, which is two to three orders lower than that of SA-based algorithms running on Intel Core-i7 CPU 7 with the main frequency of 3 GHz, as shown in Fig.  4c .

Ising computer scaling and cross-bar architecture

The above experimental demonstration shows our Ising computer with 80 SMTJs is capable of finding a near-optimal solution to a medium-scale NP-hard problem. We then explore the performance with increasing from 70 to 200 cities. The simulation of complete TSP task is carried out using MATLAB, incorporating a stochastic model of the SMTJ employed in our experiment (details in Supplementary Note  11 ). The solution quality is defined as

Figure  5a illustrates the solution quality of the best results obtained for each TSP task (Supplementary Note  12 for the best solutions). Notably, as the number of SMTJ (M) increases, higher quality solutions can be attained. It is worth emphasizing that the shortest path obtained for the 101-city TSP is 640.9755 in our study, surpassing the optimal path of 642.3095 provided by TSPLIB (Eil101.opt.tour). This outcome serves as evidence of the superiority of our method. The utilization of more SMTJs solving TSP per sliding window leads to improved optimization of CTSP annealing, resulting in an enhanced solution quality, as depicted in Fig.  5b . Consequently, the time to convergence s would also increase with the use of more SMTJS. When dealing with a fixed hardware capacity, an appropriate number of SMTJs for CTSP optimization can be assigned, taking into account both the solution quality and convergence speed. Figure  5c showcases the success rate (defined as achieving 95% solution quality) as the problem size increases. The success probability of 200-city TSP, whose complexity is ~40,000 nodes, can reach as high as 90%, demonstrating the scalability of our method compared to typical TSP (without GP and CTSP) 9 .

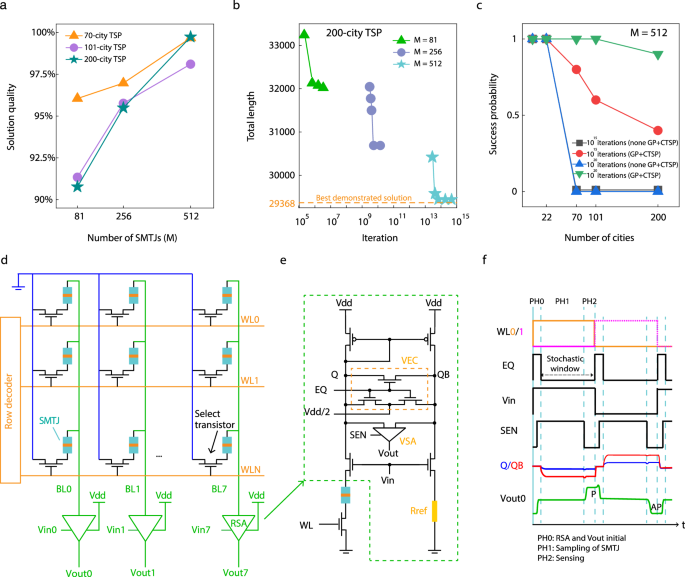
a Solution quality of various problems using different number of SMTJs (M) in the array. The datasets used are St70, Eil101 and KroA200, for 70, 101 and 200 cities, respectively. b Total length of KroA200 TSP at different convergence speeds using different number of SMTJs. The dashed line represents the best demonstrated solution. c Success probability of different TSP algorithm (without/with GP and CTSP) as the number of cities increases after running for 50 times. A total of 512 SMTJs are used. Here we define the success as achieving the solution quality of 95%. d SMTJ cross-bar array which contains row decoder, SMTJ, select transistor and read sense amplifier (RSA). BL represents bit line, WL represents word line, Vin, Vout and Vdd represent the input voltage, output voltage and supply voltage of RSA. e Circuit of one RSA which contains a current mirror, voltage equalization circuit (VEC, with a control signal of EQ which initializes the voltages in Q and QB points, under a reference voltage of Vdd/2), voltage sense amplifier (VSA, with a control signal of SEN), reference resistance ( \({{{{{\rm{Rref}}}}}}=\frac{1}{2}({{{{{\rm{Rap}}}}}}+{{{{{\rm{Rp}}}}}})\) , Rap and Rp represent SMTJ’s resistance in AP and P state respectively), and control transistors. f Signals of writing/reading two adjacent SMTJ cells in one BL, selected by WL0 and WL1 in sequence. All signals are defined in e and f .

We also propose a cross-bar architecture for large-scale Ising computer implementation, which can be integrated by using modern MRAM and CMOS technologies. The core part of this architecture consists of SMTJ bit cells organized as a cross-bar array, integrated with row decoders and read sense amplifiers (RSA), as shown in Fig.  5d . Each SMTJ bit cell contains one select transistor and one SMTJ (1T1SMTJ), whereas the gate of the select transistor is driven by word lines (WL), and the source of all bit cells are connected to the ground. Each bit line is assigned with an RSA. The current flows through SMTJ can be continuously adjusted by Vin of RSA, and the state of SMTJ can be read by RSA at the same time. Figure  5e illustrated the circuit of RSA, in which two clamp transistors control the current flow through the bit cell path and reference path by the gate voltage (Vin), and a current mirror is used to guarantee the same current of the above two paths. Then different voltages would show in the Q and QB point when the resistance of SMTJ is higher or lower than the reference resistor (Rref). By utilizing an enabled voltage sense amplifier (VSA), the voltages at the Q and QB points are sensed, allowing the SMTJ state to be determined as either Vdd (P state) or 0 V (AP state). Particularly, a voltage equalization circuit (VEC) is designed for initializing VSA to avoid incorrect readout. Electrical coupling through a resistance change 43 is evaluated to have neglectable effects (details in Supplementary Note  11 ). Figure  5f shows the signals to control and read bit cells. In phase 0 (PH0), one row of SMTJs is selected by WL, and Vin prepared by peripheral circuit is applied to the corresponding RSA. EQ is set high to initialize Q, QB and Vout as Vdd/2. In phase 1 (PH1), the SMTJ fluctuates from the falling edge to next rising edge of EQ. Finally, in phase 2 (PH2), RSAs read the data of one row in parallel at the falling edge of SEN. After the first row has been retrieved, the partial sum starts to be computed. Meanwhile, the same process for the second row can be started, so and so forth. To avoid reading the previous state, the duration of PH1 is preferred to be comparable with the retention time of SMTJ, which limits the main frequency of the system (see details in Supplementary Note  11 ).

We compare our system with other state-of-art Ising solvers, including CMOS annealer (Intel Core i7 processor) 7 , quantum annealer (D-Wave 2000Q) 16 , 17 , CIM with FPGA 26 , memristor Hopfield neural networks (mem-HNN) 44 , and phase-transition nano-oscillators (PTNO) 28 in solving 4761-node TSP70, as shown in Table  1 . We use the experimental data for benchmarking from literature, and two kinds of SMTJs for comparison. One is our perpendicular anisotropy SMTJ device and the other is assuming recently reported in-plane anisotropy SMTJ with a retention time of 8 ns 45 , 46 . The major attributes are the main frequency (defined as 1/iteration time), power, time-to-solution as well as energy efficiency (defined as solutions per second per watt). As quantum computers, CIM, mem-HNN, and PTNO only demonstrated ~100-node max-cut problems, we estimate the time-to-solution for solving TSP70 by assuming that the algorithm and the total number of spins to find a near-optimal solution is the same as our work (details in Supplementary Note  13 ). Here, we set 80-spin Ising computer as a standard and fix the number of iterations of 400,000 for a good solution to TSP70. Only Ising computing parts are calculated for power consumption.

In Table  1 , although the main frequency of CPU is the highest among all candidates, the energy efficiency is lower than our SMTJ-based approach. This is due to the redundant logic and data transfer delay between the memory and PEs in a conventional von-Neumann architecture. The SMTJ-based approach currently outperforms the quantum annealer both in the power consumption as well as time to solution. The power of quantum annealer is huge which needs to be optimized further for real applications. CIM is another promising architecture with a fast speed and acceptable power consumption. Current CIM systems are proof-of-concept systems which are not at present optimized for energy efficiency. Mem-HNN has a relatively fast speed assuming the 180-nm CMOS technology. However, the required number of devices is large, which limits the integrated density. The PTNO approach uses capacitors or resistors to mimic spin coupling, whose main frequency would be limited by the system scale and parasitic effects. It is reported that the ideal main frequency would decrease from 500 to 87 MHz when the system scale increases from 8-node to 100-node 28 . Our SMTJ-based Ising computer outperforms other approaches with low power consumption with 0.64 mW (details in Supplementary Note  13 ).

We experimentally demonstrate perpendicular MTJs with a retention time of ~0.1 ms and solve TSP70 Ising problems at an energy efficiency of 39 solutions per second per watt. Furthermore, we simulate an Ising computer with 4 Kb SMTJs using 40 nm commercial CMOS technology. The simulated energy efficiency for solving TSP70 by using the same SMTJ can reach 68 solutions per second per watt. By using reported in-plane SMTJ 45 and advanced CMOS, the system could obtain the highest energy efficiency of \(5.4\times {10}^{3}\) , which shows several orders of magnitude improvement over other approaches. This result suggests that an SMTJ-based Ising computer can be a good candidate for solving dense Ising problems in a highly energy-efficient and fast way.

In summary, we have experimentally demonstrated an intrinsic all-to-all Ising computer based on 80 SMTJs, and solved 9-city TSP with the optimal solution. Furthermore, a compressing strategy based on CTSP and GP is proposed to experimentally solve 4761-node 70-city TSP on an 80-node system with a near-optimum solution as well as ultra-low energy consumption. A cross-bar architecture is then proposed for large-scale Ising computers and the 200 city TSP task is simulated. Our system provides a feasible solution to fast, energy-efficient, and scalable Ising computing schemes to solve NP-hard problems.

Sample growth and device fabrication

Thin film samples of substrate/[W (3)/Ru (10)] 2 /W (3)/Pt (3)/Co (0.25)/Pt (0.2)/[Co (0.25)/Pt (0.5)] 5 /Co (0.6)/Ru (0.85)/Co (0.6)/Pt (0.2)/Co (0.3)/Pt (0.2)/Co (0.5)/W (0.3)/CoFeB (0.9)/MgO (1.1)/CoFeB (1.5)/Ta (3)/Ru (7)/Ta (5) were deposited via DC (metallic layers) and RF magnetron (MgO layer) sputtering on the Si substrates with thermal oxide of 300 nm with a base pressure of less than \(2\times {10}^{-8}\) Torr at room temperature. The numbers in parentheses are thicknesses in nanometers. To fabricate the superparamagnetic tunnel junctions, bottom electrode structures with a width of 10 µm were firstly patterned via photolithography and Ar ion milling. MTJ pillar structures with a diameter of ~50 nm for the superparamagnetic behavior were patterned by using e-beam lithography. The encapsulation layer of Si 3 N 4 was in-situ deposited after ion milling without breaking vacuum by using RF magnetron sputtering, and top electrode structures with a width of 10 µm were patterned via photolithography and top electrodes of Ta (5 nm)/Cu (40 nm) were deposited by using DC magnetron sputtering.

MTJ characterization by probe station

The setup includes a source meter (Keithley 2400) for supplying DC bias currents and a data acquisition card (NI-DAQmx USB-6363) for the read operation. A single SMTJ operation cycle comprises two steps (i.e. bias and read). A small DC input current with an amplitude of 1–20 μA is applied to SMTJ. Simultaneously, the DAQ card reads the voltage signal across the SMTJ at a maximum sampling rate of 2 MHz. The MTJ switching probability varies in accordance with the amplitude of applied currents. The retention time of MTJ is determined from random telegraph noise measurements over 250 ms. The expectation values of event time τ is determined by fitting an exponential function to the experimental results.

80 SMTJ arrays and peripheral circuits are integrated on a 12 cm × 15 cm PCB, controlled by an MCU (Arduino Mega 2560 Rev3). Four 12-bit rail-to-rail DACs (AD5381) with 160 output channels in total are used to generate analog DC inputs for PE and comparator arrays. Half of the DAC output channels are used to provide stimulation to the gate terminal of NMOSs (2N7002DW-G), and others are used to provide reference voltages to comparators (AD8694). The drain voltages of NMOS are compared with reference voltages and generate outputs in parallel. Outputs of comparator arrays are read by MCU through four multiplexers (FST16233) and then are calculated to obtain new inputs for DACs. The supply voltage of the PCB board and SMTJs is 5 V and 0.8 V, respectively. The value of resistors in each computing unit can be designed to adjust the center of sigmoidal curves.

Data availability

The data generated during this study are available within the article and the  Supplementary Information file.  Source data are provided with this paper.

Code availability

The codes that support this study can be available from the corresponding author upon request.

Theis, T. N. & Wong, H. S. P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 19 , 41–50 (2017).

Article   Google Scholar  

Shim, Y., Jaiswal, A. & Roy, K. Ising computation based combinatorial optimization using spin-Hall effect (SHE) induced stochastic magnetization reversal. J. Appl. Phys. 121 , 193902 (2017).

Article   ADS   Google Scholar  

Tindell, K. W., Burns, A. & Wellings, A. J. Allocating hard real-time tasks: An NP-Hard problem made easy. J. Real.-Time Syst. 4 , 145–165 (1992).

Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573 , 390–393 (2019).

Article   ADS   CAS   PubMed   Google Scholar  

Tatsumura, K., Hidaka, R., Yamasaki, M., Sakai, Y. & Goto, H. A Currency Arbitrage Machine Based on the Simulated Bifurcation Algorithm for Ultrafast Detection of Optimal Opportunity. in 2020 IEEE International Symposium on Circuits and Systems (ISCAS) 1–5 (IEEE, 2020). https://doi.org/10.1109/ISCAS45731.2020.9181114 .

Cohen, E., Carmi, M., Heiman, R., Hadar, O. & Cohen, A. Image restoration via ising theory and automatic noise estimation. In 2013 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB) 1–5 (IEEE, 2013). https://doi.org/10.1109/BMSB.2013.6621708 .

Zhou, A.-H. et al. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information 10 , 7 (2018).

Garza-Santisteban, F. et al. A Simulated Annealing Hyper-heuristic for Job Shop Scheduling Problems. In 2019 IEEE Congress on Evolutionary Computation (CEC) 57–64 (IEEE, 2019). https://doi.org/10.1109/CEC.2019.8790296 .

Lucas, A. Ising formulations of many NP problems. Front. Physics 2 , 5 (2014).

Albash, T. & Lidar, D. A. Adiabatic quantum computation. Rev. Mod. Phys. 90 , 015002 (2018).

Article   ADS   MathSciNet   Google Scholar  

Dickson, N. G. & Amin, M. H. S. Does Adiabatic Quantum Optimization Fail for NP-Complete Problems? Phys. Rev. Lett. 106 , 050502 (2011).

Article   ADS   PubMed   Google Scholar  

Heim, B., Ronnow, T. F., Isakov, S. V. & Troyer, M. Quantum versus classical annealing of Ising spin glasses. Science 348 , 215–217 (2015).

Article   ADS   MathSciNet   CAS   PubMed   Google Scholar  

Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58 , 5355–5363 (1998).

Article   ADS   CAS   Google Scholar  

Martoňák, R., Santoro, G. E. & Tosatti, E. Quantum annealing of the traveling-salesman problem. Phys. Rev. E 70 , 057701 (2004).

Okuyama, T., Hayashi, M. & Yamaoka, M. An Ising Computer Based on Simulated Quantum Annealing by Path Integral Monte Carlo Method. In 2017 IEEE International Conference on Rebooting Computing (ICRC) 1–6 (IEEE, 2017). https://doi.org/10.1109/ICRC.2017.8123652 .

Hamerly, R. et al. Experimental investigation of performance differences between Coherent Ising Machines and a quantum annealer. Sci. Adv. 5 , eaau0823 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473 , 194–198 (2011).

Yamaoka, M. et al. A 20k-Spin Ising Chip to Solve Combinatorial Optimization Problems With CMOS Annealing. IEEE J. Solid State Circuits 51 , 303–309 (2016).

Yamaoka, M. et al. 24.3 20k-spin Ising chip for combinational optimization problem with CMOS annealing. In 2015 IEEE International Solid-State Circuits Conference - (ISSCC) Digest of Technical Papers 1–3 (IEEE, 2015). https://doi.org/10.1109/ISSCC.2015.7063111 .

Davendra, D., Metlicka, M. & Bialic-Davendra, M. CUDA Accelerated 2-OPT Local Search for the Traveling Salesman Problem. In Novel Trends in the Traveling Salesman Problem (eds. Davendra, D. & Bialic-Davendra, M.) (IntechOpen, 2020). https://doi.org/10.5772/intechopen.93125 .

Tatsumura, K., Dixon, A. R. & Goto, H. FPGA-Based Simulated Bifurcation Machine. In 2019 29th International Conference on Field Programmable Logic and Applications (FPL) 59–66 (IEEE, 2019). https://doi.org/10.1109/FPL.2019.00019 .

Tatsumura, K., Yamasaki, M. & Goto, H. Scaling out Ising machines using a multi-chip architecture for simulated bifurcation. Nat. Electron 4 , 208–217 (2021).

Mathew, S. K. et al. μ RNG: A 300–950 mV, 323 Gbps/W All-Digital Full-Entropy True Random Number Generator in 14 nm FinFET CMOS. IEEE J. Solid-State Circuits 51 , 1695–1704 (2016).

Pervaiz, A. Z., Sutton, B. M., Ghantasala, L. A. & Camsari, K. Y. Weighted p-Bits for FPGA Implementation of Probabilistic Circuits. IEEE Trans. Neural Netw. Learn. Syst. 30 , 1920–1926 (2019).

Article   PubMed   Google Scholar  

McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354 , 614–617 (2016).

Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354 , 603–606 (2016).

Sutton, B., Camsari, K. Y., Behin-Aein, B. & Datta, S. Intrinsic optimization using stochastic nanomagnets. Sci. Rep. 7 , 44370 (2017).

Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron 4 , 502–512 (2021).

Sharmin, S., Shim, Y. & Roy, K. Magnetoelectric oxide based stochastic spin device towards solving combinatorial optimization problems. Sci. Rep. 7 , 11276 (2017).

Faria, R., Camsari, K. Y. & Datta, S. Implementing Bayesian networks with embedded stochastic MRAM. AIP Adv. 8 , 045101 (2018).

Zand, R., Camsari, K. Y., Datta, S. & DeMara, R. F. Composable Probabilistic Inference Networks Using MRAM-based Stochastic Neurons. J. Emerg. Technol. Comput. Syst. 15 , 1–22 (2019).

Choi, V. Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process 7 , 193–209 (2008).

Article   MathSciNet   Google Scholar  

Sugie, Y. et al. Minor-embedding heuristics for large-scale annealing processors with sparse hardware graphs of up to 102,400 nodes. Soft Comput 25 , 1731–1749 (2021).

Cai, J., Macready, W. G. & Roy, A. A practical heuristic for finding graph minors. Preprint at http://arxiv.org/abs/1406.2741 (2014).

Chaves-O’Flynn, G. D., Wolf, G., Sun, J. Z. & Kent, A. D. Thermal Stability of Magnetic States in Circular Thin-Film Nanomagnets with Large Perpendicular Magnetic Anisotropy. Phys. Rev. Appl. 4 , 024010 (2015).

Mitra, D., Romeo, F. & Sangiovanni-Vincentelli, A. Convergence and finite-time behavior of simulated annealing. Adv. Appl. Probab. 18 , 747–771 (1986).

Mills, K., Ronagh, P. & Tamblyn, I. Finding the ground state of spin Hamiltonians with reinforcement learning. Nat. Mach. Intell. 2 , 509–517 (2020).

MP-TESTDATA - The TSPLIB Symmetric Traveling Salesman Problem Instances. http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ (2013).

Dan, A., Shimizu, R., Nishikawa, T., Bian, S. & Sato, T. Clustering Approach for Solving Traveling Salesman Problems via Ising Model Based Solver. In 2020 57th ACM/IEEE Design Automation Conference (DAC) 1–6 (IEEE, 2020). https://doi.org/10.1109/DAC18072.2020.9218695 .

Ezugwu, A. E.-S., Adewumi, A. O. & Frîncu, M. E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem. Expert Syst. Appl. 77 , 189–210 (2017).

Mohsen, A. M. Annealing Ant Colony Optimization with Mutation Operator for Solving TSP. Comput. Intell. Neurosci. 2016 , 1–13 (2016).

Wang, J., Ersoy, O. K., He, M. & Wang, F. Multi-offspring genetic algorithm and its application to the traveling salesman problem. Appl. Soft Comput. 43 , 415–423 (2016).

Talatchian, P. et al. Mutual control of stochastic switching for two electrically coupled superparamagnetic tunnel junctions. Phys. Rev. B 104 , 054427 (2021).

Cai, F. et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nat. Electron 3 , 409–418 (2020).

Hayakawa, K. et al. Nanosecond Random Telegraph Noise in In-Plane Magnetic Tunnel Junctions. Phys. Rev. Lett. 126 , 117202 (2021).

Safranski, C. et al. Demonstration of Nanosecond Operation in Stochastic Magnetic Tunnel Junctions. Nano Lett. 21 , 2040–2045 (2021).

Download references

Acknowledgements

This work was supported by National Research Foundation (NRF), Prime Minister’s Office, Singapore, under its Competitive Research Programme (NRF-000214-00 to H.Y.), Advanced Research and Technology Innovation Center (ARTIC to H.Y.), the National University of Singapore under Grant (project number: A-0005947-19-00 to H.Y.), and Ministry of Education, Singapore, under Tier 2 (T2EP50123-0025 to H.Y.). We thank Yuqi Su, and Chne-Wuen Tsai from National University of Singapore and Zhi-Da Song from Peking University for useful discussions.

Author information

Authors and affiliations.

Department of Electrical and Computer Engineering, National University of Singapore, Singapore, Singapore

Jia Si, Shuhan Yang, Yunuo Cen, Jiaer Chen, Yingna Huang, Zhaoyang Yao, Dong-Jun Kim, Kaiming Cai, Jerald Yoo, Xuanyao Fong & Hyunsoo Yang

Key Laboratory for the Physics and Chemistry of Nanodevices and Center for Carbon-based Electronics, School of Electronics, Peking University, Beijing, China

You can also search for this author in PubMed   Google Scholar

Contributions

J.S. and H.Y. conceived and designed the experiments. J.S. designed, fabricated, and coded the hardware system. D.K., and S.Y. fabricated the devices. J.S., S.Y., and K.C. performed device measurements. Z.Y. bonded the components on PCB. J.S. designed SMTJ-based Ising system. J.S., J.C., Y.C., Y.H. and X.F. developed the optimization algorithm and performed simulations. J.S., S.Y., Y.C., J.Y., X.F. and H.Y. analyzed the data. J.S. and H.Y. wrote the manuscript. H.Y. proposed and supervised this work. All authors discussed the results and revised the manuscript.

Corresponding author

Correspondence to Hyunsoo Yang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information, source data, source data, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Si, J., Yang, S., Cen, Y. et al. Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems. Nat Commun 15 , 3457 (2024). https://doi.org/10.1038/s41467-024-47818-z

Download citation

Received : 16 June 2022

Accepted : 11 April 2024

Published : 24 April 2024

DOI : https://doi.org/10.1038/s41467-024-47818-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• TripAdvisor

• Testimonials
• Travel Tips

Moscow Metro Map 2005 (Official) Eng/Rus

About Me in Short

My name's Arthur Lookyanov, I'm a private tour guide, personal driver and photographer in Moscow, Russia. I work in my business and run my website Moscow-Driver.com from 2002. Read more about me and my services , check out testimonials of my former business and travel clients from all over the World, hit me up on Twitter or other social websites. I hope that you will like my photos as well.

See you in Moscow!

• View full size
• Owner: Moscow Guide & Driver
• Date: August 19, 2005 08:00:00 pm EDT
• File name: Moscow-Metro-Map-2005-Official.jpg
• Tags: Russia , Moscow Metro , maps , Moscow Metro Map , Moscow Metropolitan , Moscow

Google Maps

• GPS Map of Moscow Guide & Driver's pictures

Random image

Emperor Peter III (1762)

Portrait of Peter III (1728-1762), Emperor of Russia (5 January 1762 – 9 July 1762), wearing military uniform hoding a baton, standing beside his regalia, painted in 1762 by Alexei Antropov (1716-1795) from State Tretyakov Gallery in Moscow.

Featured Tags

• 273 photos are tagged with architecture
• 199 photos are tagged with cathedrals
• 305 photos are tagged with churches
• 294 photos are tagged with Dear Clients
• 260 photos are tagged with lights
• 1875 photos are tagged with Moscow
• 306 photos are tagged with Moscow by Night
• 194 photos are tagged with Moscow cityscapes
• 264 photos are tagged with Moscow Kremlin
• 326 photos are tagged with night moscow
• 426 photos are tagged with Orthodox Churches
• 226 photos are tagged with Red Square
• 2538 photos are tagged with Russia
• 209 photos are tagged with twilights
• 350 photos are tagged with Winter

Take one of these exciting tours:

• Moscow Highlights
• Discovering the Golden Ring of Russia
• Arts & Culture Tours
• Moscow by Night tour

Map of the 2100 Moscow Metro

July 31, 2010

Planning on taking the Moscow metro at the beginning of the next century? If so, be sure to have this map handy — it should clear things up for you:

This map — and the version detailing the current Moscow Metro , which is slightly more sane — was made by Artemy Lebedev . In all seriousness, his map of the 2010 metro is a nice improvement to the current standard .