travelling salesman problem nearest neighbor algorithm

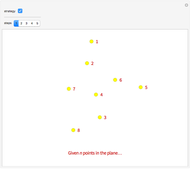
Traveling salesman problem

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Traveling_salesman_problems

Author: Jessica Yu (ChE 345 Spring 2014)

Steward: Dajun Yue, Fengqi You

The traveling salesman problem (TSP) is a widely studied combinatorial optimization problem, which, given a set of cities and a cost to travel from one city to another, seeks to identify the tour that will allow a salesman to visit each city only once, starting and ending in the same city, at the minimum cost. 1

• 2.1 Graph Theory
• 2.2 Classifications of the TSP
• 2.3 Variations of the TSP
• 3.1 aTSP ILP Formulation
• 3.2 sTSP ILP Formulation
• 4.1 Exact algorithms
• 4.2.1 Tour construction procedures
• 4.2.2 Tour improvement procedures
• 5 Applications
• 7 References

The origins of the traveling salesman problem are obscure; it is mentioned in an 1832 manual for traveling salesman, which included example tours of 45 German cities but gave no mathematical consideration. 2 W. R. Hamilton and Thomas Kirkman devised mathematical formulations of the problem in the 1800s. 2

It is believed that the general form was first studied by Karl Menger in Vienna and Harvard in the 1930s. 2,3

Hassler Whitney, who was working on his Ph.D. research at Harvard when Menger was a visiting lecturer, is believed to have posed the problem of finding the shortest route between the 48 states of the United States during either his 1931-1932 or 1934 seminar talks. 2 There is also uncertainty surrounding the individual who coined the name “traveling salesman problem” for Whitney’s problem. 2

The problem became increasingly popular in the 1950s and 1960s. Notably, George Dantzig, Delber R. Fulkerson, and Selmer M. Johnson at the RAND Corporation in Santa Monica, California solved the 48 state problem by formulating it as a linear programming problem. 2 The methods described in the paper set the foundation for future work in combinatorial optimization, especially highlighting the importance of cutting planes. 2,4

In the early 1970s, the concept of P vs. NP problems created buzz in the theoretical computer science community. In 1972, Richard Karp demonstrated that the Hamiltonian cycle problem was NP-complete, implying that the traveling salesman problem was NP-hard. 4

Increasingly sophisticated codes led to rapid increases in the sizes of the traveling salesman problems solved. Dantzig, Fulkerson, and Johnson had solved a 48 city instance of the problem in 1954. 5 Martin Grötechel more than doubled this 23 years later, solving a 120 city instance in 1977. 5 Enoch Crowder and Manfred W. Padberg again more than doubled this in just 3 years, with a 318 city solution. 5

In 1987, rapid improvements were made, culminating in a 2,392 city solution by Padberg and Giovanni Rinaldi. In the following two decades, David L. Appelgate, Robert E. Bixby, Vasek Chvátal, & William J. Cook led the cutting edge, solving a 7,397 city instance in 1994 up to the current largest solved problem of 24,978 cities in 2004. 5

Description

Graph theory.

In the context of the traveling salesman problem, the verticies correspond to cities and the edges correspond to the path between those cities. When modeled as a complete graph, paths that do not exist between cities can be modeled as edges of very large cost without loss of generality. 6 Minimizing the sum of the costs for Hamiltonian cycle is equivalent to identifying the shortest path in which each city is visiting only once.

Classifications of the TSP

The TRP can be divided into two classes depending on the nature of the cost matrix. 3,6

• Applies when the distance between cities is the same in both directions

• Applies when there are differences in distances (e.g. one-way streets)

An ATSP can be formulated as an STSP by doubling the number of nodes. 6

Variations of the TSP

Formulation

The objective function is then given by

To ensure that the result is a valid tour, several contraints must be added. 1,3

There are several other formulations for the subtour elimnation contraint, including circuit packing contraints, MTZ constraints, and network flow constraints.

aTSP ILP Formulation

The integer linear programming formulation for an aTSP is given by

sTSP ILP Formulation

The symmetric case is a special case of the asymmetric case and the above formulation is valid. 3, 6 The integer linear programming formulation for an sTSP is given by

Exact algorithms

Branch-and-bound algorithms are commonly used to find solutions for TSPs. 7 The ILP is first relaxed and solved as an LP using the Simplex method, then feasibility is regained by enumeration of the integer variables. 7

Other exact solution methods include the cutting plane method and branch-and-cut. 8

Heuristic algorithms

Given that the TSP is an NP-hard problem, heuristic algorithms are commonly used to give a approximate solutions that are good, though not necessarily optimal. The algorithms do not guarantee an optimal solution, but gives near-optimal solutions in reasonable computational time. 3 The Held-Karp lower bound can be calculated and used to judge the performance of a heuristic algorithm. 3

There are two general heuristic classifications 7 :

• Tour construction procedures where a solution is gradually built by adding a new vertex at each step
• Tour improvement procedures where a feasbile solution is improved upon by performing various exchanges

The best methods tend to be composite algorithms that combine these features. 7

Tour construction procedures

Tour improvement procedures

Applications

The importance of the traveling salesman problem is two fold. First its ubiquity as a platform for the study of general methods than can then be applied to a variety of other discrete optimization problems. 5 Second is its diverse range of applications, in fields including mathematics, computer science, genetics, and engineering. 5,6

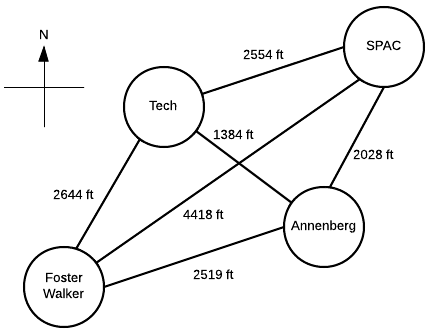
Suppose a Northwestern student, who lives in Foster-Walker , has to accomplish the following tasks:

• Drop off a homework set at Tech
• Work out a SPAC
• Complete a group project at Annenberg

Distances between buildings can be found using Google Maps. Note that there is particularly strong western wind and walking east takes 1.5 times as long.

It is the middle of winter and the student wants to spend the least possible time walking. Determine the path the student should take in order to minimize walking time, starting and ending at Foster-Walker.

Start with the cost matrix (with altered distances taken into account):

Method 1: Complete Enumeration

All possible paths are considered and the path of least cost is the optimal solution. Note that this method is only feasible given the small size of the problem.

From inspection, we see that Path 4 is the shortest. So, the student should walk 2.28 miles in the following order: Foster-Walker → Annenberg → SPAC → Tech → Foster-Walker

Method 2: Nearest neighbor

Starting from Foster-Walker, the next building is simply the closest building that has not yet been visited. With only four nodes, this can be done by inspection:

• Smallest distance is from Foster-Walker is to Annenberg
• Smallest distance from Annenberg is to Tech
• Smallest distance from Tech is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to Foster-Walker ( creates a subtour, therefore skip )
• Next smallest distance from Tech is to SPAC
• Smallest distance from SPAC is to Annenberg ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Tech ( creates a subtour, therefore skip )
• Next smallest distance from SPAC is to Foster-Walker

So, the student would walk 2.54 miles in the following order: Foster-Walker → Annenberg → Tech → SPAC → Foster-Walker

Method 3: Greedy

With this method, the shortest paths that do not create a subtour are selected until a complete tour is created.

• Smallest distance is Annenberg → Tech
• Next smallest is SPAC → Annenberg
• Next smallest is Tech → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Anneberg → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is SPAC → Tech ( creates a subtour, therefore skip )
• Next smallest is Tech → Foster-Walker
• Next smallest is Annenberg → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Annenberg ( creates a subtour, therefore skip )
• Next smallest is Tech → SPAC ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → Tech ( creates a subtour, therefore skip )
• Next smallest is SPAC → Foster-Walker ( creates a subtour, therefore skip )
• Next smallest is Foster-Walker → SPAC

So, the student would walk 2.40 miles in the following order: Foster-Walker → SPAC → Annenberg → Tech → Foster-Walker

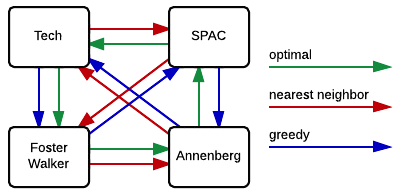
As we can see in the figure to the right, the heuristic methods did not give the optimal solution. That is not to say that heuristics can never give the optimal solution, just that it is not guaranteed.

Both the optimal and the nearest neighbor algorithms suggest that Annenberg is the optimal first building to visit. However, the optimal solution then goes to SPAC, while both heuristic methods suggest Tech. This is in part due to the large cost of SPAC → Foster-Walker. The heuristic algorithms cannot take this future cost into account, and therefore fall into that local optimum.

We note that the nearest neighbor and greedy algorithms give solutions that are 11.4% and 5.3%, respectively, above the optimal solution. In the scale of this problem, this corresponds to fractions of a mile. We also note that neither heuristic gave the worst case result, Foster-Walker → SPAC → Tech → Annenberg → Foster-Walker.

Only tour building heuristics were used. Combined with a tour improvement algorithm (such as 2-opt or simulated annealing), we imagine that we may be able to locate solutions that are closer to the optimum.

The exact algorithm used was complete enumeration, but we note that this is impractical even for 7 nodes (6! or 720 different possibilities). Commonly, the problem would be formulated and solved as an ILP to obtain exact solutions.

• Vanderbei, R. J. (2001). Linear programming: Foundations and extensions (2nd ed.). Boston: Kluwer Academic.
• Schrijver, A. (n.d.). On the history of combinatorial optimization (till 1960).
• Matai, R., Singh, S., & Lal, M. (2010). Traveling salesman problem: An overview of applications, formulations, and solution approaches. In D. Davendra (Ed.), Traveling Salesman Problem, Theory and Applications . InTech.
• Junger, M., Liebling, T., Naddef, D., Nemhauser, G., Pulleyblank, W., Reinelt, G., Rinaldi, G., & Wolsey, L. (Eds.). (2009). 50 years of integer programming, 1958-2008: The early years and state-of-the-art surveys . Heidelberg: Springer.
• Cook, W. (2007). History of the TSP. The Traveling Salesman Problem . Retrieved from http://www.math.uwaterloo.ca/tsp/history/index.htm
• Punnen, A. P. (2002). The traveling salesman problem: Applications, formulations and variations. In G. Gutin & A. P. Punnen (Eds.), The Traveling Salesman Problem and its Variations . Netherlands: Kluwer Academic Publishers.
• Laporte, G. (1992). The traveling salesman problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59 (2), 231–247.
• Goyal, S. (n.d.). A suvey on travlling salesman problem.

Navigation menu

A graph is a finite set of dots and connecting links. The dots are called vertices (a single dot is a vertex ), and the links are called edges . Each edge must connect two different vertices. A path is a connected sequence of edges showing a route on the graph that starts at a vertex and ends at a vertex. A circuit is a path that starts and ends at the same vertex. Circuits that visit each vertex once and only once are called Hamiltonian circuits .

One strategy for solving the traveling salesman problem is the nearest-neighbor algorithm . Simply stated, when given a choice of vertices this algorithm selects the nearest (i.e., least cost) neighbor.

In our applet below your goal is to select a Hamiltonian circuit using the nearest-neighbor algorithm. To start your circuit click a vertex and drag the line to an adjacent vertex. Next select the vertex with least cost (closest). Continue in this way until you have completed a Hamiltonian circuit. The Reset button will clear the current path. The New Graph button will load a new graph.

Key Products

• Route Optimization API

Optimize routing, task allocation and dispatch

• Directions and Distance Matrix API

Calculate accurate ETAs, distances and directions

• Navigation API & SDKs

Provide turn-by-turn navigation instructions

• Live Tracking API & SDKs

Track and manage assets in real time

• All Products

Product Demos

See NextBillion.ai APIs & SDKs In action

• Integrations

Easily integrate our products with your tools

Platform Overview

Learn about how Nextbillion.ai's platform is designed

Is NextBillion.ai right for you?

Understand if NextBillion.ai is right for your business

NextBillion.ai vs. Google Cloud Fleet Routing

NextBillion.ai vs. Google Distance Matrix API

NextBillion.ai vs. HERE Technologies

Technical Documentation

Snap-to-Road API

Snap GPS tracks to underlying road networks

Isochrone API

Define serviceable areas based on travel times

Optimization

Clustering API

Group data points based on their characteristics

Geofencing API

Mark virtual boundaries & track asset movements

Live Tracking SDK

Real-Time asset tracking on Mobile

Maptiles API

Create immersive visual experience for your customers

Maptiles SDK

Tailor-Made Maps for Mobile Apps

Supply Chain and Logistics

• On-Demand Delivery
• Fleet Management

E-commerce Logistics

• Field Services

Pest Control

Cleaning Services

HVAC Services

Laundry and Dry Cleaning

Ride-Hailing

Urban Mobility

Non Emergency Medical Transport

Employee Transportation

Final Mile Logistics

Public Services

Emergency Services

Waste Management

Supply Chain & Logistics

Get regulation-compliant truck routes

Solve fleet tracking, routing and navigation

• Last-Mile Delivery

Maximize fleet utilization with optimal routes

Real-time ETA calculation

• Middle Mile Delivery

Real-time ETA Calculation

• Ride Hailing

Optimized routes for cab services

• Non-Emergency Medical Transport

Optimize routing and dispatch

Field Workforce

Automate field service scheduling

• Waste Collection

Efficient route planning with road restrictions

See NextBillion.ai APIs & SDKs in Action

• Case Studies

Discover what customers are building in real time with NextBillion.ai

Join us on our upcoming virtual webinars

Whitepapers

Read through expert insights and opinions from the mapping community

Get in-depth and detailed insights

• Product Updates

Latest product releases and enhancements

Navigate the spatial world with engaging and informative content

Experience a more powerful optimization and scheduling platform, better optimized routes, advanced integration capabilities and flexible pricing with NextBillion.ai.

• NextBillion.ai vs Google Cloud Fleet Routing
• NextBillion.ai vs Google Distance Matrix API
• NextBillion.ai vs HERE Technologies

FEATURED BLOG

• API Documentation

Comprehensive API guides and references

Interactive API examples

Integrate tools you use to run your business

• Technical Blogs

Deep-dive into the technical details

Get quick answers to common queries

FEATURED TECHNICAL BLOG

How to Implement Route Optimization API using Python

Learn how to implement route optimization for vehicle fleet management using python in this comprehensive tutorial.

NEXTBILLION.AI

Partner with us

Our story, vision and mission

Meet our tribe

Latest scoop on product updates, partnerships and more

Come join us - see open positions

Reach out to us for any product- or media-related queries

For support queries, write to us at

To partner with us, contact us at

For all media-related queries, reach out to us at

For all career-related queries, reach out to us at

• Request a Demo

Best Algorithms for the Traveling Salesman Problem

• March 15, 2024

What is a Traveling Salesman Problem?

In the field of combinatorial optimization, the Traveling Salesman Problem (TSP) is a well-known puzzle with applications ranging from manufacturing and circuit design to logistics and transportation. The goal of cost-effectiveness and efficiency has made it necessary for businesses and industries to identify the best TSP solutions. It’s not just an academic issue, either. Using route optimization algorithms to find more profitable routes for delivery companies also lowers greenhouse gas emissions since fewer miles are traveled.

In this technical blog, we’ll examine some top algorithms for solving the Traveling Salesman Problem and describe their advantages, disadvantages, and practical uses.

Explore NextBillion.ai’s Route Optimization API , which uses advanced algorithms to solve TSP in real-world scenarios.

Brute Force Algorithm

The simplest method for solving the TSP is the brute force algorithm. It includes looking at every way the cities could be scheduled and figuring out how far away each approach is overall. Since it ensures that the best solution will be found, it is not useful for large-scale situations due to its time complexity, which increases equally with the number of cities.

This is a detailed explanation of how the TSP is solved by the brute force algorithm:

Create Every Permutation: Make every combination of the cities that is possible. There are a total of n! permutations to think about for n cities. Every combination shows a possible sequence where the salesman could visit the cities.

Determine the Total Distance for Every Combination: Add up the distances between each city in the permutation to find the overall distance traveled for each one. To finish the trip, consider the time from the final city to the starting point.

Determine the Best Option: Observe which permutation produces the smallest total distance and record it. This permutation represents the ideal tour. Return the most effective permutation to the TSP as the solution after examining every option.

Give back the best answer possible: Return the most effective permutation to the TSP as the solution after all possible combinations have been examined.

Even though this implementation gives an exact solution for the TSP, it becomes costly to compute for larger instances due to its time complexity, which increases factorially with the number of cities. 

The Branch-and-Bound Method

The Branch-and-Bound method can be used to solve the Traveling Salesman Problem (TSP) and other combinatorial optimization problems. To effectively find a suitable space and the best answer, divide-and-conquer strategies are combined with eliminating less-than-ideal solutions.

This is how the Branch and Bound method for the Traveling Salesman Problem works:

Start : First, give a simple answer. You could find this by starting with an empty tour or using a heuristic method.

Limit Calculation : Find the lowest total cost of the current partial solution. This limit shows the least amount of money needed to finish the tour.

Divide : Select a variable that is associated with the subsequent stage of the tour. This could mean picking out the next city to visit.

When making branches, think about the possible values for the variable you’ve chosen. Each branch stands for a different choice or option.

Cutting down : If a branch’s lower bound is higher than the best-known solution right now, cut it because you know that it can’t lead to the best solution.

Exploration : Keep using the branch-and-bound method to look into the other branches. Keep cutting and branching until all of your options have been thought through.

New Ideal Solution : Save the best solution you found while doing research. You should change the known one if a new, cheaper solution comes along.

Termination : Continue investigating until all possible paths have been considered and no more choices exist that could lead to a better solution. End the algorithm when all possible outcomes have been studied.

Selecting the order in which to visit the cities is one of the decision variables for the Traveling Salesman Problem. Usually, methods like the Held-Karp lower bound are used to calculate the lower bound. The technique identifies and cuts branches that are likely to result in less-than-ideal solutions as it carefully investigates various combinations of cities.

The Nearest Neighbor Method

A heuristic algorithm called the Nearest Neighbor method estimates solutions to the Traveling Salesman Problem (TSP). In contrast to exact methods like brute force or dynamic programming, which always get the best results, the Nearest Neighbor method finds a quick and reasonable solution by making local, greedy choices.

Here is a detailed explanation of how the nearest-neighbor method solves the TSP problem:

Starting Point : Pick a city randomly to be the tour’s starting point.

Picking Something Greedy: Select the next city on the tour to visit at each stage based on how close the current city is to the not-explored city. Usually, a selected measurement is used to calculate the distance between cities (e.g., Euclidean distance).

Go and Mark: Visit the closest city you picked, add it to your tour, and mark it as observed.

Additionally: Continue this manner until every city has been visited at least once.

Go Back to the Beginning City: After visiting all the other cities, return to the starting city to finish the tour. 

The nearest-neighbor method’s foundation is making locally optimal choices at each stage and hoping that the sum of these choices will produce a reasonable overall solution. Compared to exact algorithms, this greedy approach drastically lowers the level of computation required, which makes it appropriate for relatively large cases of the TSP.

Ant Colony Optimization

ACO, or Ant Colony Optimization, is a metaheuristic algorithm that draws inspiration from ants’ seeking habits. It works very well for resolving a combination of optimization issues, such as the TSP (Traveling Salesman Problem). The idea behind ACO is to imitate ant colonies’ chemical trail communication to determine the best routes.

Ant Colony Optimization provides the following solution for the Traveling Salesman Problem:

Starting Point: A population of synthetic ants should be planted in a random starting city. Every ant is a possible solution for the TSP.

Initialization of The scents: Give each edge in the problem space (connections between cities) an initial amount of synthetic pheromone. The artificial ants communicate with one another via the fragrance. 

Ant Motion: Each ant creates a tour by constantly selecting the next city to visit using a combination of fragrance levels and a heuristic function.

The quantity of fragrance on the edge that links the candidate city to the current city, as well as a heuristic measure that could be based on factors like distance between cities, impact the chances of selecting a specific city.

Ants mimic how real ants use chemical trails for communication by following paths with higher fragrance levels.

Update on Pheromones: The pheromone concentration on every edge is updated once every ant has finished traveling.

The update involves placing fragrances on the borders of the best tours and evaporating existing fragrances to copy the natural breakdown of chemical paths, which is intended to encourage the search for successful paths.

Repetition: For the fixed number of cycles or until a shift standard is satisfied, repeat the steps of ant movement, fragrance update, and tour construction.

Building Solution : After a few iterations, the artificial ants develop an answer, which is considered the algorithm’s outcome. This solution approximates the most efficient TSP tour.

Enhancement: To improve progress and solution quality, the process can be optimized by adjusting parameters like the influence of the heuristic function and the rate at which fragrances evaporate.

Ant Colony Optimization is excellent at solving TSP cases by using the ant population’s group ability. By striking a balance between exploration and exploitation, the algorithm can find potential paths and take advantage of success. It is a well-liked option in the heuristics field since it has been effectively used to solve various optimization issues.

Genetic Algorithm

Genetic Algorithms (GAs) are optimization algorithms derived from the concepts of genetics and natural selection. These algorithms imitate evolution to find predictions for complex problems, such as the Traveling Salesman Problem (TSP). 

Here is how genetic algorithms resolve the TSP:

Starting Point: select a starting group of possible TSP solutions. Every possible tour that visits every city exactly once is represented by each solution.

Assessment: Examine each solution’s fitness within the population. Fitness is commonly defined in the TSP environment as the opposite of the total distance traveled. Tour length is a determining factor in fitness scores.

Choice: Choose people from the population to be the parents of the following generation. Each person’s fitness level determines the likelihood of selection. More fit solutions have a higher chance of being selected.

Transformation (Recombination): To produce offspring, perform crossover, or recombination, on pairs of chosen parents. To create new solutions, crossover entails sharing information between parent solutions.

Crossover can be applied in various ways for TSP, such as order crossover (OX) or partially mapped crossover (PMX), to guarantee that the resulting tours preserve the authenticity of city visits.

Change: Change some of the offspring solutions to introduce arbitrary changes. A mutation can involve flipping two cities or changing the order of a subset of cities.

Mutations add diversity to the population when discovering new regions of the solution space. 

Substitute: Parents and children together make up the new generation of solutions that will replace the old ones. A portion of the top-performing solutions from the previous generation may be retained in the new generation as part of a privileged replacement process.

Finalization: For a predetermined number of generations or until a convergence criterion is satisfied, repeat the selection, crossover, mutation, and replacement processes. 

Enhancement: Modify variables like population size, crossover rate, and mutation rate to maximize the algorithm’s capacity to identify excellent TSP solutions.

When it comes to optimizing combinations, genetic algorithms are exceptional at sifting through big solution spaces and identifying superior answers. Because of their capacity to duplicate natural evolution, they can adjust to the TSP’s structure and find almost ideal tours. GAs are an effective tool in the field of evolutionary computation because they have been successfully applied to a wide range of optimization problems.

NextBillion.ai offers advanced Route Optimization API that solves real-life TSP and VRP problems, which can be easily integrated with your applications. 

Book a demo Today!

In this Article

About author.

Rishabh is a freelance technical writer based in India. He is a technology enthusiast who loves working in the B2B tech space.

It is not possible to solve the Traveling Salesman Problem with Dijkstra’s algorithm. Dijkstra’s algorithm, a single-source shortest path algorithm, finds the shortest possible route from a given source node to every other node in a weighted graph. In comparison, the Traveling Salesman Problem looks for the quickest route that stops in every city exactly once before returning to the starting point.

The term “traveling salesman” refers to a scenario where a salesperson visits different cities to sell goods or services. The goal of this problem is to find the shortest route that goes to each city once and returns to the starting point. It is a fundamental problem in algorithmic optimization to determine the best order of city trips and minimize travel time or distance.

“Route salesman” or just “sales representative” are other terms for a traveling salesman. These people go to various places to sell goods and services to customers. The traveling salesman, who determines the shortest route to visit multiple cities, is often referred to as a “touring agent” or simply as the “salesman” in the context of mathematical optimization.

The minimum distance a salesman needs to visit each city exactly once and then return to the starting city is known as the shortest distance in the Traveling Salesman Problem (TSP). It stands for the ideal tour duration that reduces the total travel distance. The goal of solving the TSP, an essential issue in combinatorial optimization, is finding the shortest distance.

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

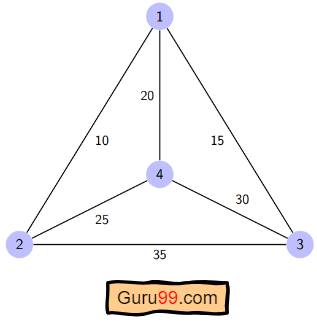
Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

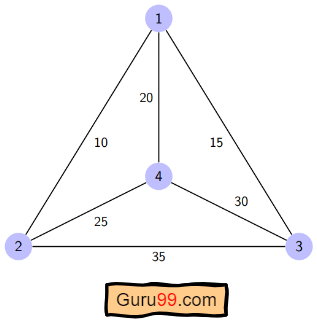
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

For the given figure, the adjacency matrix would be the following:

Let’s see how our algorithm works:

Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

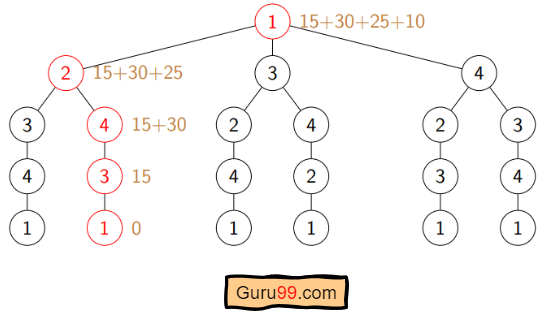
Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)
• Kadence’s Algorithm: Largest Sum Contiguous Subarray
• Radix Sort Algorithm in Data Structure
• Doubly Linked List: C++, Python (Code Example)
• Singly Linked List in Data Structures
• Adjacency List and Matrix Representation of Graph

Algorithms for the Travelling Salesman Problem

Printables.com

• The Travelling Salesman Problem (TSP) is a classic algorithmic problem in the field of computer science and operations research, focusing on optimization. It seeks the shortest possible route that visits every point in a set of locations just once.
• The TSP problem is highly applicable in the logistics sector , particularly in route planning and optimization for delivery services. TSP solving algorithms help to reduce travel costs and time.
• Real-world applications often require adaptations because they involve additional constraints like time windows, vehicle capacity, and customer preferences.
• Advances in technology and algorithms have led to more practical solutions for real-world routing problems. These include heuristic and metaheuristic approaches that provide good solutions quickly.
• Tools like Routific use sophisticated algorithms and artificial intelligence to solve TSP and other complex routing problems, transforming theoretical solutions into practical business applications.

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest possible route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one — the one that will require the least distance or cost — is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem in graph theory. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm for solving travelling salesman problems in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

The main problem can be solved by calculating every permutation using a brute force approach, and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially, soon surpassing the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

TThe brute-force approach, also known as the naive approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the brute-force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one — this is the optimal solution. 

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route beyond the first pair of cities, one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the traveling salesman problem.

3. The nearest neighbor method

To implement the nearest neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the nearest neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the nearest neighbor algorithm serves as a good starting point for tackling the traveling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition. ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

• Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
• Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP. 
• Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization. 
• Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used. 
• Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II. 
• Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource. 

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, approximate solutions — often produced using artificial intelligence and machine learning — are useful in all verticals.

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.

Minimizing costs in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

What is a hamiltonian cycle, and why is it important in solving the travelling salesman problem.

A Hamiltonian cycle is a complete loop that visits every vertex in a graph exactly once before returning to the starting vertex. It's crucial for the TSP because the problem essentially seeks to find the shortest Hamiltonian cycle that minimizes travel distance or time.

What role does linear programming play in solving the Travelling Salesman Problem?

Linear programming (LP) is a mathematical method used to optimize a linear objective function, subject to linear equality and inequality constraints. In the context of TSP, LP can help in formulating and solving relaxation of the problem to find bounds or approximate solutions, often by ignoring the integer constraints (integer programming being a subset of LP) to simplify the problem.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion involves a function calling itself to solve smaller sub-problems of the same type as the larger problem. In TSP, recursion is used in methods like the "Divide and Conquer" strategy, breaking down the problem into smaller, manageable subsets, which can be particularly useful in dynamic programming solutions. It reduces redundancy and computation time, making the problem more manageable.

Why is understanding time complexity important when studying the Travelling Salesman Problem?

Time complexity refers to the computational complexity that describes the amount of computer time it takes to solve a problem. For TSP, understanding time complexity is crucial because it helps predict the performance of different algorithms, especially given that TSP is NP-hard and solutions can become impractically slow as the number of cities increases.

Related articles

Liked this article? See below for more recommended reading!

Solving the Vehicle Routing Problem (2024)

How To Optimize Multi-Stop Routes With Google Maps (2024)

How Route Optimization Impacts Our Earth

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring

Traveling Salesman Problem (TSP) Implementation

• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Similar reads.

• NP Complete

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• ENGINEERING
• What's the point?
• life cycles
• engineering
• data visualization
• biogeochemistry
• social science
• computer science
• epidemiology

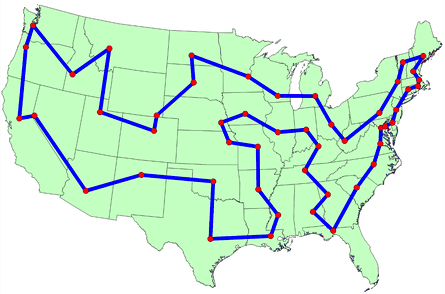
11 Animated Algorithms for the Traveling Salesman Problem

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action.

TSP Algorithms and heuristics

Although we haven’t been able to quickly find optimal solutions to NP problems like the Traveling Salesman Problem, "good-enough" solutions to NP problems can be quickly found [1] .

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action. Researchers often use these methods as sub-routines for their own algorithms and heuristics. This is not an exhaustive list.

For ease of visual comparison we use Dantzig49 as the common TSP problem, in Euclidean space. Dantzig49 has 49 cities — one city in each contiguous US State, plus Washington DC.

1: Greedy Algorithm

A greedy algorithm is a general term for algorithms that try to add the lowest cost possible in each iteration, even if they result in sub-optimal combinations.

In this example, all possible edges are sorted by distance, shortest to longest. Then the shortest edge that will neither create a vertex with more than 2 edges, nor a cycle with less than the total number of cities is added. This is repeated until we have a cycle containing all of the cities.

Although all the heuristics here cannot guarantee an optimal solution, greedy algorithms are known to be especially sub-optimal for the TSP.

2: Nearest Neighbor

The nearest neighbor heuristic is another greedy algorithm, or what some may call naive. It starts at one city and connects with the closest unvisited city. It repeats until every city has been visited. It then returns to the starting city.

Karl Menger, who first defined the TSP, noted that nearest neighbor is a sub-optimal method:

"The rule that one first should go from the staring point to the closest point, then to the point closest to this, etc., in general does not yield the shortest route."

The time complexity of the nearest neighbor algorithm is O(n^2) . The number of computations required will not grow faster than n^2.

3: Nearest Insertion

Insertion algorithms add new points between existing points on a tour as it grows.

One implementation of Nearest Insertion begins with two cities. It then repeatedly finds the city not already in the tour that is closest to any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible. It stops when no more insertions remain.

The nearest insertion algorithm is O(n^2)

4: Cheapest Insertion

Like Nearest Insertion, Cheapest Insertion also begins with two cities. It then finds the city not already in the tour that when placed between two connected cities in the subtour will result in the shortest possible tour. It inserts the city between the two connected cities, and repeats until there are no more insertions left.

The cheapest insertion algorithm is O(n^2 log2(n))

5: Random Insertion

Random Insertion also begins with two cities. It then randomly selects a city not already in the tour and inserts it between two cities in the tour. Rinse, wash, repeat.

Time complexity: O(n^2)

6: Farthest Insertion

Unlike the other insertions, Farthest Insertion begins with a city and connects it with the city that is furthest from it.

It then repeatedly finds the city not already in the tour that is furthest from any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible.

7: Christofides Algorithm

Christofides algorithm is a heuristic with a 3/2 approximation guarantee. In the worst case the tour is no longer than 3/2 the length of the optimum tour.

Due to its speed and 3/2 approximation guarantee, Christofides algorithm is often used to construct an upper bound, as an initial tour which will be further optimized using tour improvement heuristics, or as an upper bound to help limit the search space for branch and cut techniques used in search of the optimal route.

For it to work, it requires distances between cities to be symmetric and obey the triangle inequality, which is what you'll find in a typical x,y coordinate plane (metric space). Published in 1976, it continues to hold the record for the best approximation ratio for metric space.

The algorithm is intricate [2] . Its time complexity is O(n^4)

A problem is called k-Optimal if we cannot improve the tour by switching k edges.

Each k-Opt iteration takes O(n^k) time.

2-Opt is a local search tour improvement algorithm proposed by Croes in 1958 [3] . It originates from the idea that tours with edges that cross over aren’t optimal. 2-opt will consider every possible 2-edge swap, swapping 2 edges when it results in an improved tour.

2-opt takes O(n^2) time per iteration.

3-opt is a generalization of 2-opt, where 3 edges are swapped at a time. When 3 edges are removed, there are 7 different ways of reconnecting them, so they're all considered.

The time complexity of 3-opt is O(n^3) for every 3-opt iteration.

10: Lin-Kernighan Heuristic

Lin-Kernighan is an optimized k-Opt tour-improvement heuristic. It takes a tour and tries to improve it.

By allowing some of the intermediate tours to be more costly than the initial tour, Lin-Kernighan can go well beyond the point where a simple 2-Opt would terminate [4] .

Implementations of the Lin-Kernighan heuristic such as Keld Helsgaun's LKH may use "walk" sequences of 2-Opt, 3-Opt, 4-Opt, 5-Opt, “kicks” to escape local minima, sensitivity analysis to direct and restrict the search, as well as other methods.

LKH has 2 versions; the original and LKH-2 released later. Although it's a heuristic and not an exact algorithm, it frequently produces optimal solutions. It has converged upon the optimum route of every tour with a known optimum length. At one point in time or another it has also set records for every problem with unknown optimums, such as the World TSP, which has 1,900,000 locations.

11: Chained Lin-Kernighan

Chained Lin-Kernighan is a tour improvement method built on top of the Lin-Kernighan heuristic:

Lawrence Weru

Larry is a TEDx speaker, Harvard Medical School Dean's Scholar, Florida State University "Notable Nole," and has served as an invited speaker at Harvard, FSU, and USF. Larry's contributions are featured by Harvard University, Fast Company, and Gizmodo Japan, and cited in books by Routledge and No Starch Press. His stories and opinions are published in Slate, Vox, Toronto Star, Orlando Sentinel, and Vancouver Sun, among others. He illustrates the sciences for a more just and sustainable world.

You might also like

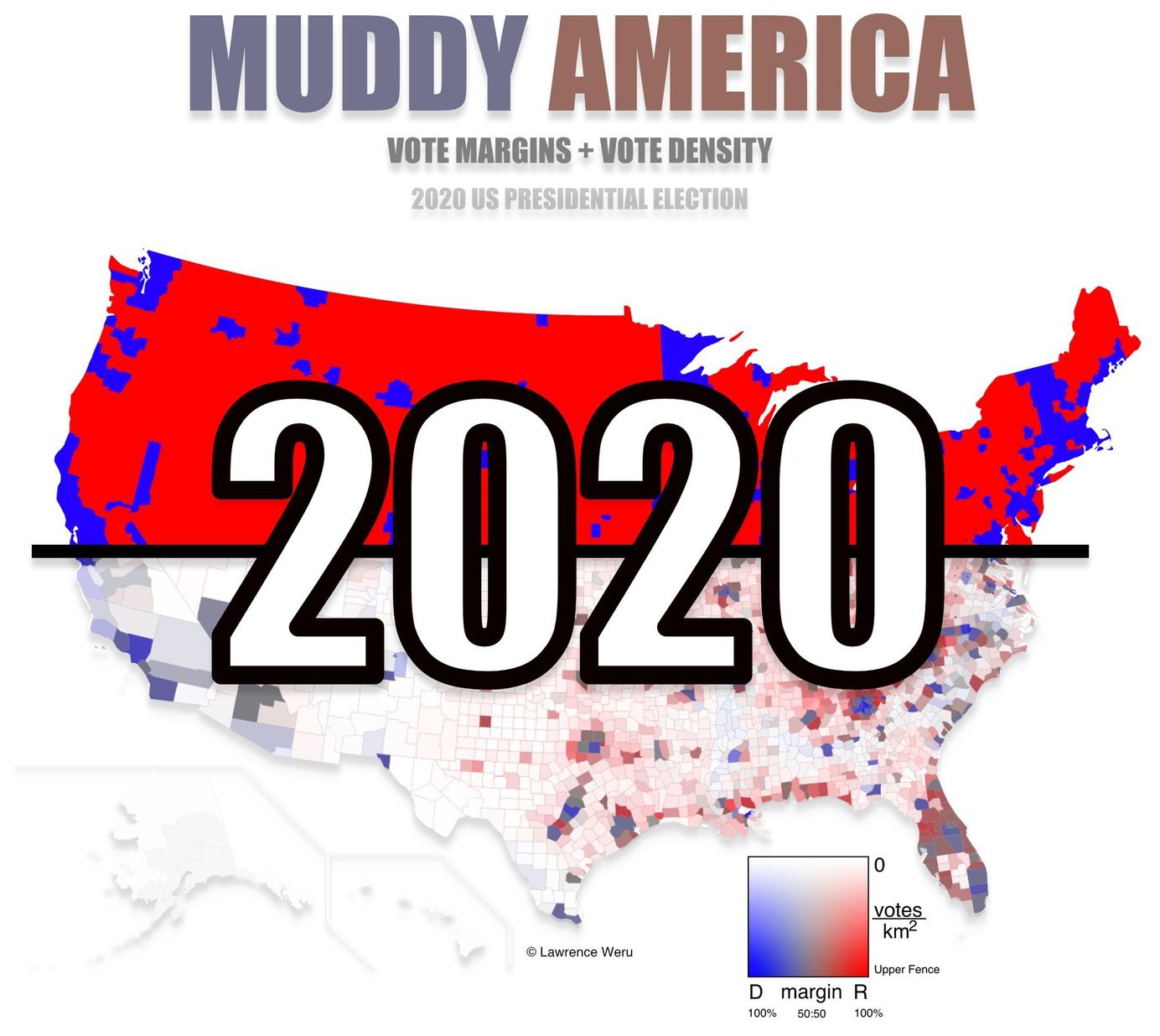
2020 Presidential Election County Level Muddy Map Paid Members Public

2020 US Presidential Election Interactive County-Level Vote Map

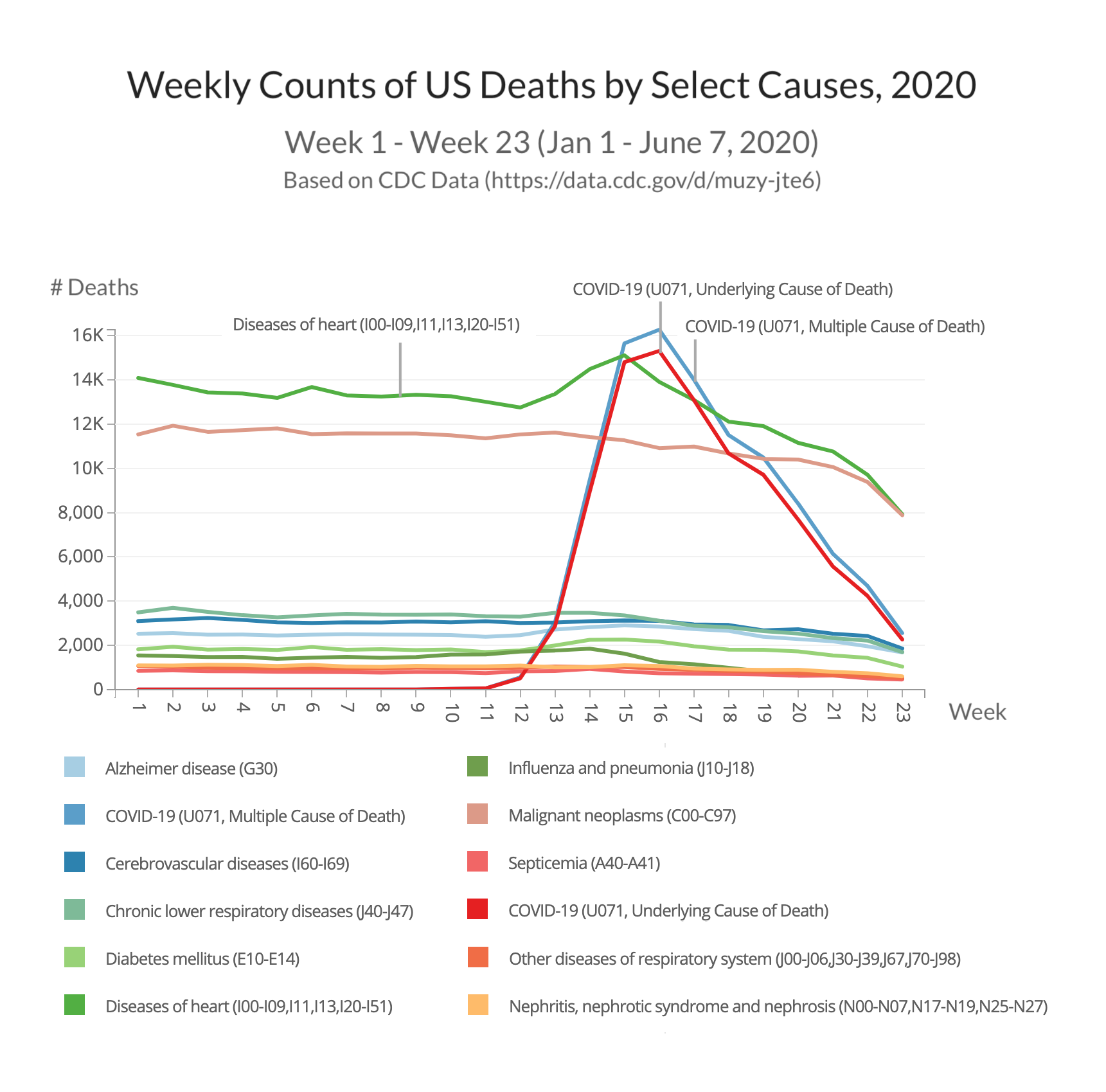
Weekly Counts of US Deaths by Select Causes through June 2020 Paid Members Public

This graph uses CDC data to compare COVID deaths with other causes of deaths.

STEM Lounge Newsletter

Be the first to receive the latest updates in your inbox.

Featured Posts

Tokyo olympics college medal count 🏅.

Muddy America : Color Balancing The US Election Map - Infographic

The trouble with the purple election map.

This website uses cookies to ensure you get the best experience on our website. You may opt out by using any cookie-blocking technology, such as your browser add-on of choice. Got it!

Wolfram Demonstrations Project

The traveling salesman problem 3: nearest neighbor heuristic.

• Open in Cloud
• Download to Desktop
• Copy Resource Object

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products .

Do not show again

Because of its simplicity, the nearest neighbor heuristic is one of the first algorithms that comes to mind in attempting to solve the traveling salesman problem (TSP), in which a salesman has to plan a tour of cities that is of minimal length. In this heuristic, the salesman starts at some city and then visits the city nearest to the starting city, and so on, only taking care not to visit a city twice. At the end all cities are visited and the salesman returns to the starting city.

This Demonstration displays nearest neighbor tours (use the step slider to see them) along with a better tour computed by the built-in Mathematica function FindShortestTour , forming the outline of the blue polygon. All nearest neighbor tours start at point 1.

There is a moment at which some points are "forgotten" during the course of the algorithm, and they have to be inserted at a great cost in the end. Though usually rather bad, nearest neighbor tours have the advantage that they only contain a few severe mistakes while being very fast and easy to implement. Therefore, such tours can serve as good starting tours that other methods can improve.

Contributed by: Jaime Rangel-Mondragon   (July 2012) Open content licensed under CC BY-NC-SA

[1] E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan, and D. B. Shmoys, eds., The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization , New York: John Wiley & Sons, 1985.

Related Links

• Traveling Salesman Problem  ( Wolfram MathWorld )
• Traveling Salesman Problem
• Finding the Shortest Traveling Salesman Tour
• Comparing Algorithms for the Traveling Salesman Problem

Permanent Citation

Jaime Rangel-Mondragon "The Traveling Salesman Problem 3: Nearest Neighbor Heuristic" http://demonstrations.wolfram.com/TheTravelingSalesmanProblem3NearestNeighborHeuristic/ Wolfram Demonstrations Project Published: July 30 2012

Share Demonstration

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Topics

• Combinatorics
• Graph Theory
• Optimization

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: Hamiltonian Circuits and the Traveling Salesman Problem

• Last updated
• Save as PDF
• Page ID 85482

• David Lippman
• Pierce College via The OpenTextBookStore

In the last section, we considered optimizing a walking route for a postal carrier. How is this different than the requirements of a package delivery driver? While the postal carrier needed to walk down every street (edge) to deliver the mail, the package delivery driver instead needs to visit every one of a set of delivery locations. Instead of looking for a circuit that covers every edge once, the package deliverer is interested in a circuit that visits every vertex once.

Hamilton Circuits and Paths

A Hamiltonian circuit is a circuit that visits every vertex once with no repeats. Being a circuit, it must start and end at the same vertex. A Hamiltonian path also visits every vertex once with no repeats, but does not have to start and end at the same vertex.

Hamiltonian circuits are named for William Rowan Hamilton who studied them in the 1800’s.

One Hamiltonian circuit is shown on the graph below. There are several other Hamiltonian circuits possible on this graph. Notice that the circuit only has to visit every vertex once; it does not need to use every edge.

This circuit could be notated by the sequence of vertices visited, starting and ending at the same vertex: ABFGCDHMLKJEA. Notice that the same circuit could be written in reverse order, or starting and ending at a different vertex.

Unlike with Euler circuits, there is no nice theorem that allows us to instantly determine whether or not a Hamiltonian circuit exists for all graphs.[1]

Does a Hamiltonian path or circuit exist on the graph below?

We can see that once we travel to vertex E there is no way to leave without returning to C, so there is no possibility of a Hamiltonian circuit. If we start at vertex E we can find several Hamiltonian paths, such as ECDAB and ECABD.

Depending on the problem being solved, sometimes weights are assigned to the edges. The weights could represent the distance between two locations, the travel time, or the travel cost.

With Hamiltonian circuits, our focus will not be on existence, but on the question of optimization; given a graph where the edges have weights, can we find the optimal Hamiltonian circuit; the one with lowest total weight.

To answer this question of how to find the lowest cost Hamiltonian circuit, we will consider some possible approaches. The first option that might come to mind is to just try all different possible circuits.

Brute Force Algorithm (a.k.a. exhaustive search)

• List all possible Hamiltonian circuits
• Find the length of each circuit by adding the edge weights
• Select the circuit with minimal total weight.

Apply the Brute force algorithm to find the minimum cost Hamiltonian circuit on the graph below.

To apply the Brute force algorithm, we list all possible Hamiltonian circuits and calculate their weight:

\(\begin{array}{|l|l|} \hline \textbf { Circuit } & \textbf { Weight } \\ \hline \text { ABCDA } & 4+13+8+1=26 \\ \hline \text { ABDCA } & 4+9+8+2=23 \\ \hline \text { ACBDA } & 2+13+9+1=25 \\ \hline \end{array}\)

Note: These are the unique circuits on this graph. All other possible circuits are the reverse of the listed ones or start at a different vertex, but result in the same weights.

From this we can see that the second circuit, ABDCA, is the optimal circuit.

The Brute force algorithm is optimal; it will always produce the Hamiltonian circuit with minimum weight. Is it efficient? To answer that question, we need to consider how many Hamiltonian circuits a graph could have. For simplicity, let’s look at the worst-case possibility, where every vertex is connected to every other vertex. This is called a complete graph. In figure A, there are examples of complete graphs with different numbers of vertices.

Out of convenience, mathematicians sometimes use specific notation for complete graphs based on the number of vertices. A complete graph with \(n\) vertices can be represented by K n . For example, the graphs represented above are K 2 , K 3 , K 5 and K 9 .

Suppose we had a complete graph with five vertices like the air travel graph above. From Seattle there are four cities we can visit first. From each of those, there are three choices. From each of those cities, there are two possible cities to visit next. There is then only one choice for the last city before returning home.

This can be shown visually:

Counting the number of routes, we can see there are \(4 \cdot 3 \cdot 2 \cdot 1=24\) routes. For six cities there would be \(5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\) routes.

Number of Possible Circuits

For \(n\) vertices in a complete graph, there will be \((n-1) !=(n-1)(n-2)(n-3) \cdots 3 \cdot 2 \cdot 1\) routes. Half of these are duplicates in reverse order, so there are \(\frac{(n-1) !}{2}\) unique circuits.

The exclamation symbol, !, is read “factorial” and is shorthand for the product shown.

How many circuits would a complete graph with 8 vertices have?

A complete graph with 8 vertices would have \((8-1) !=7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=5040\) possible Hamiltonian circuits. Half of the circuits are duplicates of other circuits but in reverse order, leaving 2520 unique routes.

While this is a lot, it doesn’t seem unreasonably huge. But consider what happens as the number of cities increase:

\(\begin{array}{|l|l|} \hline \textbf { Cities } & \textbf { Unique Hamiltonian Circuits } \\ \hline 9 & 8 ! / 2=20,160 \\ \hline 10 & 9 ! / 2=181,440 \\ \hline 11 & 10 ! / 2=1,814,400 \\ \hline 15 & 14 ! / 2=43,589,145,600 \\ \hline 20 & 19 ! / 2=60,822,550,204,416,000 \\ \hline \end{array}\)

As you can see the number of circuits is growing extremely quickly. If a computer looked at one billion circuits a second, it would still take almost two years to examine all the possible circuits with only 20 cities! Certainly Brute Force is not an efficient algorithm.

Unfortunately, no one has yet found an efficient and optimal algorithm to solve the TSP, and it is very unlikely anyone ever will. Since it is not practical to use brute force to solve the problem, we turn instead to heuristic algorithms ; efficient algorithms that give approximate solutions. In other words, heuristic algorithms are fast, but may or may not produce the optimal circuit.

Nearest Neighbor Algorithm (NNA)

• Select a starting point.
• Move to the nearest unvisited vertex (the edge with smallest weight).
• Repeat until the circuit is complete.

Consider our earlier graph, shown to the right.

From D, the nearest neighbor is C, with a weight of 8.

From C, our only option is to move to vertex B, the only unvisited vertex, with a cost of 13.

From B we return to A with a weight of 4.

The resulting circuit is ADCBA with a total weight of \(1+8+13+4 = 26\).

We ended up finding the worst circuit in the graph! What happened? Unfortunately, while it is very easy to implement, the NNA is a greedy algorithm, meaning it only looks at the immediate decision without considering the consequences in the future. In this case, following the edge AD forced us to use the very expensive edge BC later.

• LA to Chicago: $100
• Chicago to Atlanta: $75
• Atlanta to Dallas: $85
• Dallas to Seattle: $120

Total cost: $450

In this case, nearest neighbor did find the optimal circuit.

Going back to our first example, how could we improve the outcome? One option would be to redo the nearest neighbor algorithm with a different starting point to see if the result changed. Since nearest neighbor is so fast, doing it several times isn’t a big deal.

Repeated Nearest Neighbor Algorithm (RNNA)

• Do the Nearest Neighbor Algorithm starting at each vertex
• Choose the circuit produced with minimal total weight

Starting at vertex A resulted in a circuit with weight 26.

Starting at vertex B, the nearest neighbor circuit is BADCB with a weight of 4+1+8+13 = 26. This is the same circuit we found starting at vertex A. No better.

Starting at vertex C, the nearest neighbor circuit is CADBC with a weight of 2+1+9+13 = 25. Better!

Starting at vertex D, the nearest neighbor circuit is DACBA. Notice that this is actually the same circuit we found starting at C, just written with a different starting vertex.

The RNNA was able to produce a slightly better circuit with a weight of 25, but still not the optimal circuit in this case. Notice that even though we found the circuit by starting at vertex C, we could still write the circuit starting at A: ADBCA or ACBDA.

Try it Now 1

The table below shows the time, in milliseconds, it takes to send a packet of data between computers on a network. If data needed to be sent in sequence to each computer, then notification needed to come back to the original computer, we would be solving the TSP. The computers are labeled A-F for convenience.

\(\begin{array}{|l|l|l|l|l|l|l|} \hline & \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{D} & \mathrm{E} & \mathrm{F} \\ \hline \mathrm{A} & \_ \_ & 44 & 34 & 12 & 40 & 41 \\ \hline \mathrm{B} & 44 & \_ \_ & 31 & 43 & 24 & 50 \\ \hline \mathrm{C} & 34 & 31 & \_ \_ & 20 & 39 & 27 \\ \hline \mathrm{D} & 12 & 43 & 20 & \_ \_ & 11 & 17 \\ \hline \mathrm{E} & 40 & 24 & 39 & 11 & \_ \_ & 42 \\ \hline \mathrm{F} & 41 & 50 & 27 & 17 & 42 & \_ \_ \\ \hline \end{array}\)

a. Find the circuit generated by the NNA starting at vertex B.

b. Find the circuit generated by the RNNA.

At each step, we look for the nearest location we haven’t already visited.

From B the nearest computer is E with time 24.

From E, the nearest computer is D with time 11.

From D the nearest is A with time 12.

From A the nearest is C with time 34.

From C, the only computer we haven’t visited is F with time 27

From F, we return back to B with time 50.

The NNA circuit from B is BEDACFB with time 158 milliseconds.

While certainly better than the basic NNA, unfortunately, the RNNA is still greedy and will produce very bad results for some graphs. As an alternative, our next approach will step back and look at the “big picture” – it will select first the edges that are shortest, and then fill in the gaps.

Cheapest Edge Algorithm (Best Edge/Greedy Algorithm)

1. Select the cheapest unused edge in the graph.

2. Repeat step 1, adding the cheapest unused edge to the circuit, unless:

a. adding the edge would create a circuit that doesn’t contain all vertices, or

b. adding the edge would give a vertex degree 3.

3. Repeat until a circuit containing all vertices is formed.

Using the four vertex graph from earlier, we can use the Sorted Edges algorithm.

The cheapest edge is AD, with a cost of 1. We highlight that edge to mark it selected.

The next shortest edge is AC, with a weight of 2, so we highlight that edge.

For the third edge, we’d like to add AB, but that would give vertex A degree 3, which is not allowed in a Hamiltonian circuit. The next shortest edge is CD, but that edge would create a circuit ACDA that does not include vertex B, so we reject that edge. The next shortest edge is BD, so we add that edge to the graph.

Notice that the algorithm did not produce the optimal circuit in this case; the optimal circuit is ACDBA with weight 23.

While the Sorted Edge algorithm overcomes some of the shortcomings of NNA, it is still only a heuristic algorithm, and does not guarantee the optimal circuit.

Your teacher’s band, Derivative Work , is doing a bar tour in Oregon. The driving distances are shown below. Plan an efficient route for your teacher to visit all the cities and return to the starting location. Use NNA starting at Portland, and then use Sorted Edges.

\( \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline & & & & & & & & & & \\ & \text { Ashland } & \text { Astoria } & \text { Bend } & \text { Corvallis } & \text { Crater Lake } & \text { Eugene } & \text { Newport } & \text { Portland } & \text { Salem } & \text { Seaside } \\ \hline \text { Ashland } & \_ & 374 & 200 & 223 & 108 & 178 & 252 & 285 & 240 & 356 \\ \hline \text { Astoria } & 374 & \_ & 255 & 166 & 433 & 199 & 135 & 95 & 136 & 17 \\ \hline \text { Bend } & 200 & 255 & \_ & 128 & 277 & 128 & 180 & 160 & 131 & 247 \\ \hline \text { Corvallis } & 223 & 166 & 128 & \_ & 430 & 47 & 52 & 84 & 40 & 155 \\ \hline \text { Crater Lake } & 108 & 433 & 277 & 430 & \_ & 453 & 478 & 344 & 389 & 423 \\ \hline \text { Eugene } & 178 & 199 & 128 & 47 & 453 & \_ & 91 & 110 & 64 & 181 \\ \hline \text { Newport } & 252 & 135 & 180 & 52 & 478 & 91 & \_ & 114 & 83 & 117 \\ \hline \text { Portland } & 285 & 95 & 160 & 84 & 344 & 110 & 114 & \_ & 47 & 78 \\ \hline \text { Salem } & 240 & 136 & 131 & 40 & 389 & 64 & 83 & 47 & \_ & 118 \\ \hline \text { Seaside } & 356 & 17 & 247 & 155 & 423 & 181 & 117 & 78 & 118 & \_ \\ \hline \end{array}\)

Using NNA with a large number of cities, you might find it helpful to mark off the cities as they’re visited to keep from accidently visiting them again. Looking in the row for Portland, the smallest distance is 47, to Salem. Following that idea, our circuit will be:

Using Sorted Edges, you might find it helpful to draw an empty graph, perhaps by drawing vertices in a circular pattern. Adding edges to the graph as you select them will help you visualize any circuits or vertices with degree 3.

We start adding the shortest edges:

The graph after adding these edges is shown to the right. The next shortest edge is from Corvallis to Newport at 52 miles, but adding that edge would give Corvallis degree 3.

Continuing on, we can skip over any edge pair that contains Salem or Corvallis, since they both already have degree 2.

The graph after adding these edges is shown to the right. At this point, we can skip over any edge pair that contains Salem, Seaside, Eugene, Portland, or Corvallis since they already have degree 2.

At this point the only way to complete the circuit is to add:

Crater Lk to Astoria 433 miles

The final circuit, written to start at Portland, is:

Portland, Salem, Corvallis, Eugene, Newport, Bend, Ashland, Crater Lake, Astoria, Seaside, Portland.

Total trip length: 1241 miles.

While better than the NNA route, neither algorithm produced the optimal route. The following route can make the tour in 1069 miles:

Portland, Astoria, Seaside, Newport, Corvallis, Eugene, Ashland, Crater Lake, Bend, Salem, Portland

Try it Now 2

Find the circuit produced by the Sorted Edges algorithm using the graph below.

AB: Add, cost 11

BG: Add, cost 13

AE: Add, cost 14

EC: Skip (degree 3 at E)

FG: Skip (would create a circuit not including C)

BF, BC, AG, AC: Skip (would cause a vertex to have degree 3)

GC: Add, cost 36

CF: Add, cost 37, completes the circuit

Final circuit: ABGCFEA

[1] There are some theorems that can be used in specific circumstances, such as Dirac’s theorem, which says that a Hamiltonian circuit must exist on a graph with n vertices if each vertex has degree n /2 or greater.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 24 April 2024

Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems

• Jia Si   ORCID: orcid.org/0000-0003-0737-4905 1 , 2 ,
• Shuhan Yang 1 ,
• Yunuo Cen 1 ,
• Jiaer Chen 1 ,
• Yingna Huang 1 ,
• Zhaoyang Yao 1 ,
• Dong-Jun Kim 1 ,
• Kaiming Cai 1 ,
• Jerald Yoo   ORCID: orcid.org/0000-0002-3150-1727 1 ,
• Xuanyao Fong   ORCID: orcid.org/0000-0001-5939-7389 1 &
• Hyunsoo Yang   ORCID: orcid.org/0000-0003-0907-2898 1  

Nature Communications volume  15 , Article number:  3457 ( 2024 ) Cite this article

1539 Accesses

4 Altmetric

Metrics details

• Electrical and electronic engineering
• Magnetic devices

The growth of artificial intelligence leads to a computational burden in solving non-deterministic polynomial-time (NP)-hard problems. The Ising computer, which aims to solve NP-hard problems faces challenges such as high power consumption and limited scalability. Here, we experimentally present an Ising annealing computer based on 80 superparamagnetic tunnel junctions (SMTJs) with all-to-all connections, which solves a 70-city traveling salesman problem (TSP, 4761-node Ising problem). By taking advantage of the intrinsic randomness of SMTJs, implementing global annealing scheme, and using efficient algorithm, our SMTJ-based Ising annealer outperforms other Ising schemes in terms of power consumption and energy efficiency. Additionally, our approach provides a promising way to solve complex problems with limited hardware resources. Moreover, we propose a cross-bar array architecture for scalable integration using conventional magnetic random-access memories. Our results demonstrate that the SMTJ-based Ising computer with high energy efficiency, speed, and scalability is a strong candidate for future unconventional computing schemes.

Similar content being viewed by others

Efficient combinatorial optimization by quantum-inspired parallel annealing in analogue memristor crossbar

Combinatorial optimization by weight annealing in memristive hopfield networks

Ferroelectric compute-in-memory annealer for combinatorial optimization problems

Introduction.

The demands for future data-intensive and energy-efficient computing tasks overwhelm the computational power of conventional von Neumann architectures 1 . For example, NP-hard problems are often encountered in combinatorial optimizations 2 , resource allocation 3 , cryptography 4 , finance 5 , image processing 6 , tour planning 7 , and job sequencing 8 , and their computational time and hardware resources increase exponentially with the problem size, which makes them very difficult or impossible to be solved by conventional computers in a finite time. These problems can be mapped to the Ising model, a mathematical model to characterize interactions between magnetic spins 9 . The dynamics of the model is algorithm- based, i.e. by constructing a proper coupling matrix and allowing the system to evolve utilizing an intrinsic convergence property of the Ising model, the ground state could be obtained as a solution to the corresponding problems. However, as the system might be trapped in many local minima, the annealing process has usually been adopted in Ising computers to address such limitations. It is commonly agreed that adding fluctuations prevents the Ising computer from being stuck at the local minima.

Efficient algorithms and hardware systems for finding an optimal or near-optimal solution of an Ising model at a fast speed and low power have been sought. Adiabatic quantum computing (AQC) 10 , 11 and quantum computing 12 , 13 , 14 , 15 based on superconducting qubits are capable of converging the Ising model by tunneling out of local minima to the global minima. A 100-node Maxcut problem was solved using a quantum computer of 2048 spins with huge power consumption 16 . Besides the high cost and complexity of cryogenic temperature, this proof-of-concept system was limited by the sparse connections only between the nearest neighbors, which leads to sub-optimal outcomes 17 . Simulated annealing based on CMOS implementations was exploited for parallel Ising computing, including central processing units (CPU) 18 , 19 , graphics processing units (GPU) 20 , and field-programmable gate array (FPGA) 21 , 22 . These hardware have reported as large as 16,384 spins, however, it requires huge hardware resources for generating random numbers to introduce stochasticity to escape from the local minima 4 , 18 , 23 , 24 . Coherent Ising machine (CIM) is an optical scheme with competitive energy efficiency. However, it requires a long fiber ring cavity and relies on external FPGA for implementing coupling 25 , 26 . The temporal multiplexing process is also time-consuming and hard to expand to large systems. Recently, experiments and simulation works have investigated various devices to emulate the behavior of Ising spins by taking advantage of their intrinsic physics. An 8-spin asynchronous probabilistic computer based on superparamagnetic tunnel junctions for solving integer factorization tasks of values up to 945 was demonstrated 4 . SPICE simulations of 16-city TSP using simulated annealing method were presented 27 . Other works such as 8-spin phase-transition nano-oscillators 28 , multiferroic oxide devices with a high thermal stability 29 , and magnetoresistive random access memory (MRAM) 30 , 31 have also conceptually proved that spin-based devices are suitable for representing Ising units. However, these works have encountered challenges in either partially-connected Ising spins or small scalability which limit the Ising computer from solving practical problems.

TSP discussed in this paper is a well-known problem which is much beyond the limitation of locally connected Ising models. Other combinatorial optimization problems, such as knapsack problems, coloring problems, and number partitioning, need all-to-all connection to satisfy specific constraints 9 . In practice, an additional graph embedding process is often required when mapping to 2-dimensional CMOS circuitry which only considered the coupling between adjacent spins 32 , 33 , 34 . Since the embedding increases the required number of auxiliary spins and causes spin connections to change, the annealing accuracy is degraded significantly, especially when the problem size is large. This means that supporting a fully connected Ising model is highly recommended for dealing with a wide range of problems. Another problem is the rapidly increasing connectivity when considering large-scale systems, which usually results in huge energy consumption and latency. Since the number of spins that a particular annealing processor can handle limit the scale of the problem that can be solved, how to solve complex problems with limited hardware in an energy-efficient way has also drawn significant attention.

In this work, we experimentally report a scalable Ising computer based on 80 SMTJs with all-to-all connections and successfully solve the 4761-node TSP problem. The intrinsic stochasticity in SMTJ enables ultra-fast and low-power Ising annealing without using extra resources for random number generation and Metropolis determining process 7 . By combining global annealing with intrinsic annealing in SMTJ, the convergence of the Ising problem is guaranteed especially in large-scale Ising problems. The method to determine parameters of global annealing is discussed. With an all-to-all connection among Ising spins, the combinatorial optimization of 9-city TSP is solved with the optimal solution. We further develop the algorithm for constrained TSP (CTSP) with no extra auxiliary Ising bits both in algorithm and hardware, indicating the superiority and flexibility of this Ising computer. Furthermore, we propose an optimization strategy based on graph partitioning (GP) and CTSP and experimentally solved a 70-city TSP, which typically needs 4761 nodes, on our 80-node Ising computer with a near-optimal solution. The system can obtain the lowest power consumption of 0.64 mW as well as high energy efficiency of 39 solutions per second per watt among state-of-art Ising annealers. We have experimentally demonstrated that large-scale Ising problems can be solved by small-scale hardware in an energy-efficient way.

SMTJ-based artificial Ising spin

Various NP-hard problems can be solved by constructing corresponding Ising models and observing the ground states during evolution processes. Figure  1a shows an all-to-all connected Ising model, whose Ising Hamiltonian can be written as

where \(H\) is the total energy of the system, \(N\) is the total number of spins, \({s}_{i}\) is the \(\,i\) -th spin with one of two states; “+1” (Ising spin up) or “−1” (Ising spin down), \({J}_{i,j}\) is the coefficient of coupling between the \(i\) -th and the \(j\) -th spins, and \({h}_{i}\) is the external field of the \(\,i\) -th spin. For a fixed configuration of other spins than \({s}_{k}\) , the probability of \({s}_{k}\) staying in the down-state is given by

where \(\Lambda=\frac{\partial H}{\partial {s}_{k}}\) (see Supplementary Note  1 ).

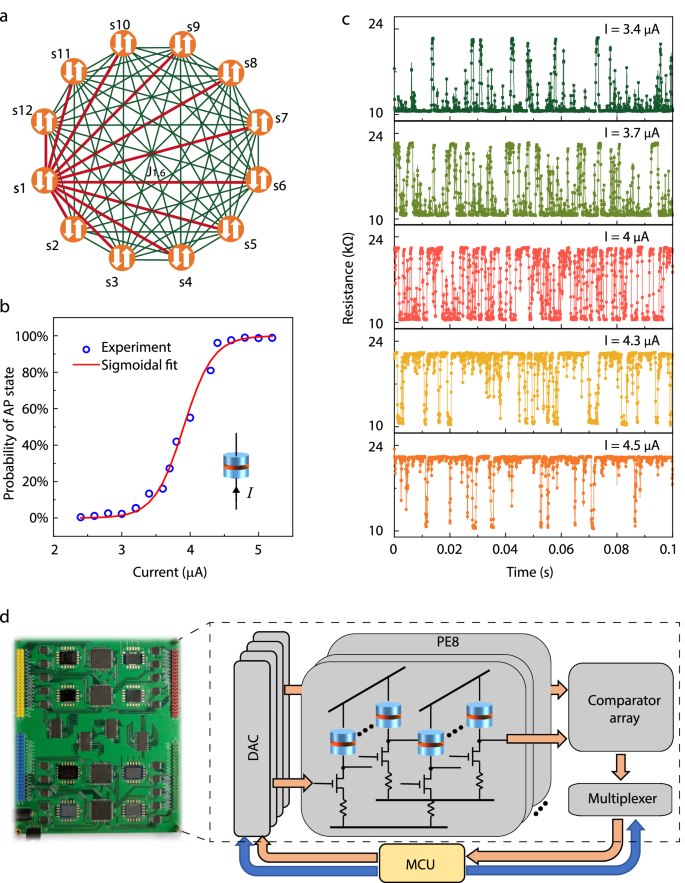
a All-to-all connected 12-spin Ising model with s represents the spin and J 1,6 represents the coupling between s1 and s6. b Sigmoidal fit of probability of AP state ( \({p}_{{AP}}\) ) of an SMTJ under different input currents ( I ). \({p}_{{{{{{\rm{AP}}}}}}}=\frac{1}{1+{e}^{-4.672\times (I-3.905{{{{{\rm{\mu }}}}}}{{{{{\rm{A}}}}}})}}\) . Inset: diagram of an SMTJ. A tunneling barrier layer is sandwiched by a reference layer and a free layer. c Time-dependent resistance of an SMTJ under different input currents ( I ). d Photograph and schematic diagram of SMTJ-based Ising computer. The system contains 8 processing elements (PEs), 4 digital-to-analog converters (DACs), a comparator array, a multiplexer and a microcontroller unit (MCU). Each PE has 10 SMTJ computing units. Each computing unit includes a transistor and a resistor to adjust the property into stochastic. Blue lines and orange arrows represent the control and data flow, respectively.

One natural implementation of this Ising spin is based on a stochastic nanomagnet. The inset of Fig.  1b shows the sketch of an SMTJ, consisting of a tunneling barrier sandwiched by a reference layer and a free layer (see Methods section). Because of the small device diameter (~50 nm), the energy barrier of the free layer between the anti-parallel (AP) and parallel (P) states is low that the retention time of either state is in the range of μs to ms, similar to previous studies 4 , 35 . The SMTJ resistance, measured as a function of time in Fig.  1c , shows preferred AP states at high currents and P states at low currents. When the current ( I ) is ~4 μA, SMTJ shows an equal chance of AP and P states. The probability of the AP state under different input currents over 0.1 s is fitted in Fig.  1b by a sigmoid function:

where \({{{{{\rm{a}}}}}}=4.67 \, {{{{{\rm{and\; b}}}}}}=3.9 \, {{{{{\rm{\mu }}}}}}{{{{{\rm{A}}}}}}.\) In order to emulate Ising spin \({s}_{k}\) with our SMTJ device, we only need to make the probability of the down-state of \({s}_{k}\) to be equal to that for the AP state of SMTJ, namely \({p}{\_}{{{{{{\rm{\_}}}}}}{{{{{\rm{AP}}}}}}}={p}{\_}{{{{{{\rm{\_}}}}}}\downarrow }\) , with two calibration coefficients. Thus, we can derive the form of the current \({{I\_}}_{k}\) injected to SMTJ as (see Supplementary Note  1 ):

where \(c=1/{kT}\) is the effective inverse temperature which can be conducted for global annealing.

Intrinsic annealing in SMTJs-based Ising computer

By integrating 80 SMTJs with a peripheral circuit and a microcontroller unit (MCU), we build an 80-node Ising computer (see Supplementary Note  2 ). Each Ising spin in Eq. ( 1 ) is emulated by an SMTJ with intrinsic randomness, where P (AP) state represents spin-up (down). Figure  1d shows the photograph of the printed circuit board (PCB) and the diagram of the system (see Methods section). The system contains 8 processing elements (PEs); each PE has 10 SMTJ computing units. Each SMTJ computing unit includes a transistor and a resistor to adjust the state of SMTJ into stochastic. During the computing process, an MCU examines the states of all SMTJs by reading the output of comparator arrays through multiplexers and generates new input voltages for digital-to-analog converters (DACs) according to the updating rule in Eq. ( 4 ) (see Supplementary Note  3 for calibration of 80 SMTJ computing units).

During the evolution process, an Ising solver could be easily trapped in a local minimum state. To avoid this non-optimal solution, annealing algorithms such as simulated annealing (SA) or quantum annealing (QA) were developed. The general idea of SA is to make the system evolve from a high temperature to a low temperature gradually 7 . The convergence and relaxation of SA can be mathematically provable 36 . During each iteration, a random number is generated for stochasticity and introduced to determine whether the result in this iteration should be accepted or not. In QA, quantum fluctuations cause quantum tunneling between states 17 . In both SA and QA, stochasticity needs to be introduced into the annealing process. In contrast, our Ising system utilizes the intrinsic stochastic behaviors of SMTJ to perform the Metropolis process of standard SA in hardware, which greatly saves the solution time and hardware resources for generating randomness (see Supplementary Note  4 ). Besides, our Ising computer has an all-to-all connection which has wider application scenarios, as well as a better capability of escaping from local minima.

Ising mapping of N-city TSP and CTSP

We have applied our Ising computer to the TSP problem, one of the combinatorial optimization problems, which applies to various sectors, such as vehicle routing, logistics, planning, and scheduling. The goal is to find the shortest route that visits all listed cities once and only once given distances between the cities in the list. In order to solve this problem, we first map N -city-TSP to an \({N}^{2}\) -spin Ising model, or \({(N-1)}^{2}\) -spin model assuming a fixed starting city. Figure  2a shows the coordinates of 9 cities and Fig.  2b shows the 81-spin Ising model, whose rows indicate the cities and columns indicate the visiting order. We define the binary spin, s , as \({s}_{i,j}\)  = 1 if city i is visited as j -th city or \({s}_{i,j}\)  = −1 otherwise. The total Hamiltonian of TSP is expressed by 9

where the first term is a constraint that represents only one city is visited at the j -th visit, and the second term represents one city is visited only one time. \(w\) is a constant small enough ( \(0 \, < \, w \, < \, 1\) ) not to violate the two constraints of the TSP cycle. \({d}_{i,{i{{\hbox{'}}}}}\) is the distance between city \(i\) and city \({i{{\hbox{'}}}}\) . According to Eqs. ( 1 ) and ( 5 ), coupling matrix \(J\) of 81 spins could be obtained, as shown in Fig.  2c (see Supplementary Note  5 ). It shows that spins in the same row or column have strong coupling, as indicated by the first two terms in Eq. ( 5 ).

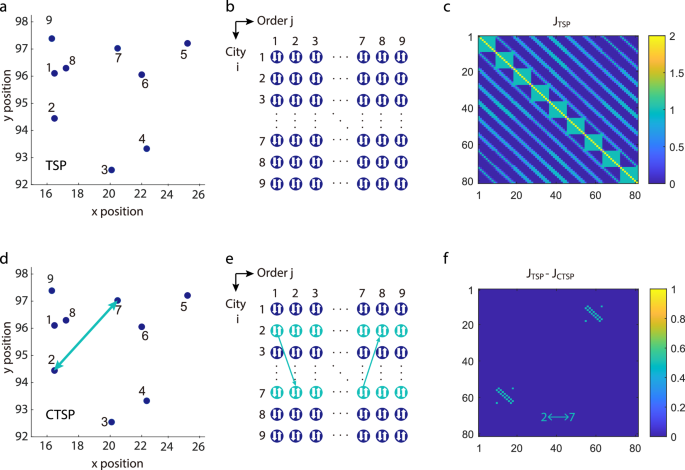
a Coordinates of all 9 cities used in this problem which are the first 9 cities in the dataset Burma14 from TSPLIB. b Ising spin representation for 9-city TSP (81 spins). Rows indicate names of cities and columns indicate the visiting order. Each spin can be 1 (visited) or −1 (not visited) in each iteration. c Color map of the coupling matrix J TSP of 9-city TSP, and the color bar represents an effective energy with the unit of kT . Here, k is the Boltzmann constant and T is the temperature. d Constrained TSP (CTSP) with a fixed vising sequence from city 2 to city 7 or from city 7 to city 2. The arrows represent the visiting sequence. e The Ising spin representation for CTSP with the fixed visiting sequence in d . Arrows represent possible vising sequences. f Color map of the difference of coupling matrix between TSP (J TSP ) in a and CTSP (J CTSP ) in d . Arrows represent the fixed vising sequences from city 2 to city 7 or from city 7 to 2.

We define CTSP as the visiting orders of some cities are enforced during the traveling. This is quite useful in real-life scenarios. For example, a delivery man collects food and drinks at shop A and must deliver hot drinks to B first even though the total cost is higher than optimal. We propose an algorithm for solving CTSP by adding negative “distance” to the Hamiltonian. For example, suppose that city A and city B are required to be connected in the CTSP as city 2 and city 7 shown in Fig.  2d , and then we add the term

such that the energy of a path, where city A and city B are connected, is always lowered by \(\theta .\) When \(\theta\) is sufficiently large, the optimal path must have city 2 and city 7 connected. Thus, the total Hamiltonian of the CTSP is expressed by

Constructing an Ising model for CTSP is exactly the same as TSP except for extra allowed visiting sequences, as shown in Fig.  2e . This would lead to a modification of the coupling matrix of \(J\) according to Eq. ( 7 ) (see the deduction of \({J}_{{CTSP}}\) in Supplementary Note  6 ). From Fig.  2f we can clearly see the differences between \({J}_{{CTSP}}\) and \({J}_{{TSP}}\) . This algorithm of CTSP fits for arbitrary constraints of visiting sequences as well as their combinations.

Experimental demonstration of 9-city TSP

We first run a 9-city TSP in the 80 SMTJ-based Ising computer at a relatively low but non-zero effective temperature to examine the intrinsic annealing in SMTJ. The iteration time is set comparable to the longest retention time of SMTJs to avoid reading previous spin states. In our experiments, we set the iteration time as 0.1 ms. As shown in Fig.  3a , as the effective inverse temperature ( c ) is increased quickly to 0.5, the system converges rapidly to a low energy state within 50 iterations and reaches the ground state after 4000 iterations. It should be noted that the intrinsic stochasticity in SMTJs helps the system escape from local minima without an extra annealing process, as shown in the right inset of Fig.  3a . Figure  3b illustrates the evolution of 9 spins out of 81 spins. The evolution of all 81 spins can be found in Supplementary Note  7 .

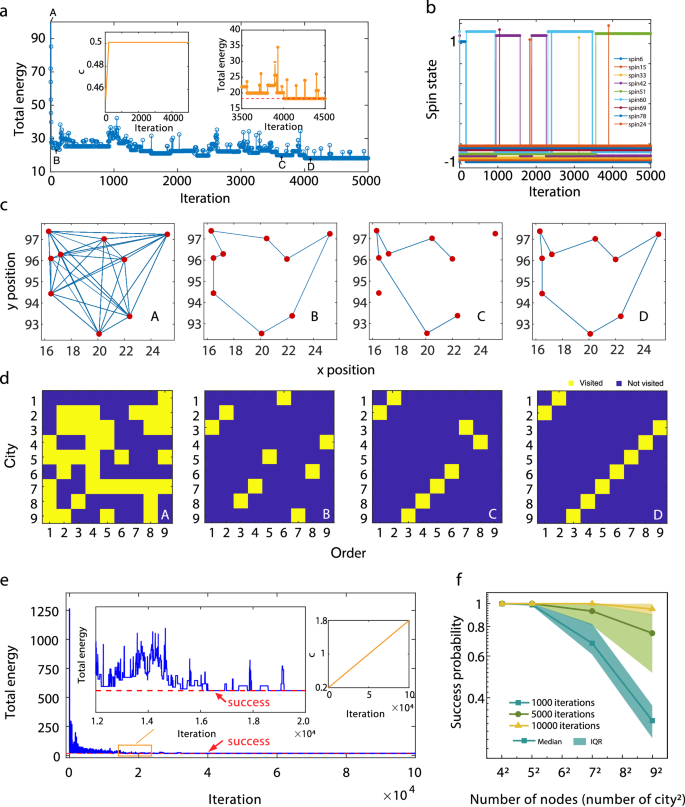
a Total energy transition of 9-city TSP with 5000 iterations (the optimal solution with the energy of 18.23 corresponds to the dashed horizontal line). Insets: effective inverse temperature ( c ) and total energy within 3500–4500 iterations. b Evolution of 9 representative SMTJ states in 5000 iterations. An offset is used in the y -axis to show each SMTJ clearly. c Visiting routes of state A, B, C, and D in a . d Corresponding Ising spins of state A, B, C, and D in a . The yellow squares represent ‘visited ( \({s}_{i,j}=1\) )’ and the purple squares represent ‘not visited ( \({s}_{i,j}=-1\) )’. e Total energy transition with increasing c from 0.2 to 1.8. Left inset: zoom-in view of total energy transition with increasing c from 0.392 to 0.52. Right inset: transition of c with iterations. The red dashed line represents the optimal path (success). f Success probability of solving TSP with varying the node size. The data points and shadows represent the median value and the interquartile range (IQR), respectively.

We choose four states in Fig.  3a to inspect the traveling path in Fig.  3c and their Ising spins, namely \({s}_{i,j}\) , as shown in Fig.  3d . The yellow square in Fig.  3d represents \({s}_{i,j}=1\) (visited) and the blue square represents \({s}_{i,j}=-1\) (not visited). In an initial state A, the spin states are randomly set and then converge to a relatively low energy at state B. State C is an intermediate solution during the annealing process. State D is the optimal solution satisfying two constraints of the TSP. Because we anneal the system to a relatively low but non-zero temperature so that the convergence to a sub-optimal state could be guaranteed, and at the same time, the intrinsic randomness in SMTJ helps the system to escape from local minima and find a ground state quickly. We test 10 different random initial states each with 5000 iterations and find that in all cases the system can obtain a relatively small energy, as shown in Supplementary Note  8 . However, there is a probability that the system jumps out of the ground state because of the non-zero temperature. If we continue to observe the evolution in a large timescale, the system would move back to the global minimum state. In some cases, where the speed and near-optimal solution matter but the accurate optimal solution is not, the number of iterations can be chosen to be small.

Further global annealing of the system to a lower effective temperature may guarantee the convergence of the computation. Here we use linear annealing as an example to examine the convergence of this algorithm in a very large-iteration limit. The initial temperature should be chosen sufficiently high to ensure that the thermal energy exceeds any energy barrier ( \(\Delta H{=H}_{\max }-{H}_{\min }\) ) within the system, while still adhering to the fundamental constraints of the specific Ising model. For a given N-city TSP, \({H}_{\max }\) in Eq. ( 5 ) can be estimated as \(w\times N\times \bar{d}\) , assuming that the distance between any two cities is the same as the average distance \(\bar{d}\) . Similarly, \({H}_{\min }\) can be estimated as \(w\times N\times {d}_{\min }\) . Therefore, the initial \(c\) of 9-city TSP in our experiment can be estimated as \({c}_{{{{{{\rm{initial}}}}}}}\, \sim 1/\Delta H=0.07\) , where \(w=0.5\) , \(N=9\) for a total of 9 cities, \(\bar{d}=4\) and \({d}_{\min }=0.8\) for the average and shortest distance of each two cities, respectively in Fig.  3c . We then choose \({c}_{{{{{{\rm{initial}}}}}}}\)  = 0.2 which is sufficiently safe for annealing. As the temperature linearly decreases, the dynamical system gradually stabilizes. The final temperature should be low enough i.e., \({c}_{{{{{{\rm{final}}}}}}} \, \gg \, 1/\Delta H\) , to freeze all possible fluctuations. Here we set \({c}_{{{{{{\rm{final}}}}}}}=1.8\) which is at least one order larger than \(1/\Delta H\) . This can also be verified by observing randomly generated states under \({c}_{{{{{{\rm{final}}}}}}}\) for long iterations. Regarding the annealing speed, if several changes in the spin configuration are observed under each value of c , then this annealing speed is valid. Plenty trials are required to find the proper annealing speed (details in Supplementary Note  8 ).

In Fig.  3e we can find the first global minimum energy appears after 16,500 iterations, and converge to the ground state after 40,000 iterations. Temperature schedules can be optimized to reduce iteration numbers, e.g. increase the effective temperature in the first few time steps, and then decrease gradually, or learned by the reinforcement learning method 37 . In practice, we use one memory to store the minimum energy state during the computation, and another memory to record the final energy state. We take the minimum value of these two results as the solution. Figure  3f shows the success probability (defined as finding the optimal path) of TSP with various node sizes. The success probability of 9-city TSP reaches 95% after 10 4 iterations. The success probability with the parameter \(w\) in Eq. ( 5 ) which determines the relative strength of the constrain term and distance term is also discussed. If the \(w\) is too large, then the probabilities of violations, namely the invalid path, would increase, as shown in Supplementary Note  8 . If \(w\) is too small, then the effect of the distance term is small, which results in a slower convergence to the ground state.

The advantages of this annealer are threefold: (1) Selective working modes by using different temperature schemes. One is the probabilistic sampling mode working at a constant temperature, which is similar to an asynchronous probabilistic computer 4 ; the other is the annealing mode conducted by reducing the effective temperature. (2) Fast speed and low power consumption to find the ground state because of the intrinsic annealing properties in SMTJ. (3) Global annealing outperforms probabilistic sampling in achieving efficient convergence, especially for large-scale problems.

We have implemented a synchronous design with a lower requirement on the speed of peripheral circuits. This design also effectively mitigates issues such as leakage, sneak currents, and parasitic resistances which might encountered in asynchronous hardware with a memristive (or resistive) crossbar array.

Compressing 70-city TSP to 80-node Ising computer

Generally, the number of spins required for an N -city TSP is ( N -1) 2 , which limits the scalability of TSP on state-of-the-art computing systems. Here, we propose a graph Ising compressing algorithm based on CTSP that can significantly reduce the number of spins and interactions for solving a TSP. Figure  4a is an example of how we apply this algorithm to our 80-node SMTJ Ising computer for solving a 70-city TSP (4761 nodes, st70 data set from TSPLIB 38 ). The major steps of this algorithm can be described as follows: (a) divide the cities into several smaller groups until the number of cities in each group is less than 10 by GP method; (b) solve TSP within each group separately; (c) integrate neighboring groups to obtain an initial path of the whole group; and (d) optimize the path in (c) by a CTSP window sliding over the whole map.

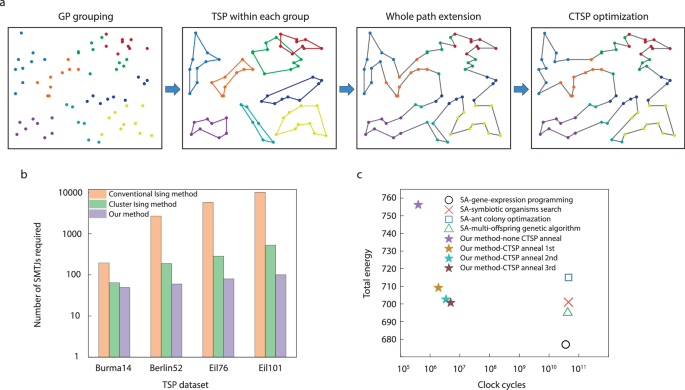
a Optimization algorithm for 70-city TSP. b Number of required SMTJs for various problems using different methods. Burma14, berlin52, eil76, and eil101 are TSP of 14, 52, 76, and 101 cities, respectively. c Comparison of total Ising energy (path) and total clock cycles for final solution with different SA-based algorithms, including symbiotic organisms search 40 , ant colony optimazation 41 , multi-offspring genetic algorithm 42 , and gene-expression programming 7 . Our method is tested on our Ising system and others are tested on Intel Core-i7 PC. In this comparison, our system runs at a main frequency of 10 kHz.

It is worth mentioning that GP is also an Ising problem. When converting a global TSP into local TSPs, using GP would be more hardware-friendly for our Ising computer compared to other clustering algorithms. It is based on the idea that the original graph can be separated into multiple sub-graphs depending on the Euclidean distance. The number of spins required for solving GP is ~ N and thus, GP is quite efficient for local TSPs since the problem size can be reduced to ~ \({\left(N-1\right)}^{2}/a\) , where \(a\) is the number of groups, and each TSP can be optimized independently (see GP mapping in Supplementary Note  9 ).

The final step (d) is based on CTSP, where a rectangular window slides over the path and cuts it into several disconnected lines, among which the two longest lines are chosen and the edge cities are connected as a circular path (Supplementary Note  10 ). The CTSP is solved within each window for sub-area optimization without changing the visiting order of edge cities. After this, the two lines at the edge cities are opened and CTSP is carried out again after sliding to the next window. GP-CTSP-based optimization algorithm provides an efficient way of finding near-optimal solutions for large-scale TSP on limited hardware resources.

Figure  4b shows the comparison of numbers of spins for different TSPs by a conventional Ising method 9 , cluster Ising method 39 , and our method. The required number of spins in our method is relatively unchanged for various TSPs, while that of other methods increases substantially with the scale of the problem. Figure  4c shows the total path of 70-city TSP as a function of iteration number using different SA-based algorithms, including symbiotic organisms search 40 , ant colony optimization 41 , multi-offspring genetic algorithm 42 , and gene-expression programming 7 . Finally, we obtain the near-optimal path with a total energy of 700.71, which is slightly higher than the optimal solution of 675. However, the iteration number for an optimized solution is 4.9 \(\times\) 10 6 by our method, which is two to three orders lower than that of SA-based algorithms running on Intel Core-i7 CPU 7 with the main frequency of 3 GHz, as shown in Fig.  4c .

Ising computer scaling and cross-bar architecture

The above experimental demonstration shows our Ising computer with 80 SMTJs is capable of finding a near-optimal solution to a medium-scale NP-hard problem. We then explore the performance with increasing from 70 to 200 cities. The simulation of complete TSP task is carried out using MATLAB, incorporating a stochastic model of the SMTJ employed in our experiment (details in Supplementary Note  11 ). The solution quality is defined as

Figure  5a illustrates the solution quality of the best results obtained for each TSP task (Supplementary Note  12 for the best solutions). Notably, as the number of SMTJ (M) increases, higher quality solutions can be attained. It is worth emphasizing that the shortest path obtained for the 101-city TSP is 640.9755 in our study, surpassing the optimal path of 642.3095 provided by TSPLIB (Eil101.opt.tour). This outcome serves as evidence of the superiority of our method. The utilization of more SMTJs solving TSP per sliding window leads to improved optimization of CTSP annealing, resulting in an enhanced solution quality, as depicted in Fig.  5b . Consequently, the time to convergence s would also increase with the use of more SMTJS. When dealing with a fixed hardware capacity, an appropriate number of SMTJs for CTSP optimization can be assigned, taking into account both the solution quality and convergence speed. Figure  5c showcases the success rate (defined as achieving 95% solution quality) as the problem size increases. The success probability of 200-city TSP, whose complexity is ~40,000 nodes, can reach as high as 90%, demonstrating the scalability of our method compared to typical TSP (without GP and CTSP) 9 .

a Solution quality of various problems using different number of SMTJs (M) in the array. The datasets used are St70, Eil101 and KroA200, for 70, 101 and 200 cities, respectively. b Total length of KroA200 TSP at different convergence speeds using different number of SMTJs. The dashed line represents the best demonstrated solution. c Success probability of different TSP algorithm (without/with GP and CTSP) as the number of cities increases after running for 50 times. A total of 512 SMTJs are used. Here we define the success as achieving the solution quality of 95%. d SMTJ cross-bar array which contains row decoder, SMTJ, select transistor and read sense amplifier (RSA). BL represents bit line, WL represents word line, Vin, Vout and Vdd represent the input voltage, output voltage and supply voltage of RSA. e Circuit of one RSA which contains a current mirror, voltage equalization circuit (VEC, with a control signal of EQ which initializes the voltages in Q and QB points, under a reference voltage of Vdd/2), voltage sense amplifier (VSA, with a control signal of SEN), reference resistance ( \({{{{{\rm{Rref}}}}}}=\frac{1}{2}({{{{{\rm{Rap}}}}}}+{{{{{\rm{Rp}}}}}})\) , Rap and Rp represent SMTJ’s resistance in AP and P state respectively), and control transistors. f Signals of writing/reading two adjacent SMTJ cells in one BL, selected by WL0 and WL1 in sequence. All signals are defined in e and f .

We also propose a cross-bar architecture for large-scale Ising computer implementation, which can be integrated by using modern MRAM and CMOS technologies. The core part of this architecture consists of SMTJ bit cells organized as a cross-bar array, integrated with row decoders and read sense amplifiers (RSA), as shown in Fig.  5d . Each SMTJ bit cell contains one select transistor and one SMTJ (1T1SMTJ), whereas the gate of the select transistor is driven by word lines (WL), and the source of all bit cells are connected to the ground. Each bit line is assigned with an RSA. The current flows through SMTJ can be continuously adjusted by Vin of RSA, and the state of SMTJ can be read by RSA at the same time. Figure  5e illustrated the circuit of RSA, in which two clamp transistors control the current flow through the bit cell path and reference path by the gate voltage (Vin), and a current mirror is used to guarantee the same current of the above two paths. Then different voltages would show in the Q and QB point when the resistance of SMTJ is higher or lower than the reference resistor (Rref). By utilizing an enabled voltage sense amplifier (VSA), the voltages at the Q and QB points are sensed, allowing the SMTJ state to be determined as either Vdd (P state) or 0 V (AP state). Particularly, a voltage equalization circuit (VEC) is designed for initializing VSA to avoid incorrect readout. Electrical coupling through a resistance change 43 is evaluated to have neglectable effects (details in Supplementary Note  11 ). Figure  5f shows the signals to control and read bit cells. In phase 0 (PH0), one row of SMTJs is selected by WL, and Vin prepared by peripheral circuit is applied to the corresponding RSA. EQ is set high to initialize Q, QB and Vout as Vdd/2. In phase 1 (PH1), the SMTJ fluctuates from the falling edge to next rising edge of EQ. Finally, in phase 2 (PH2), RSAs read the data of one row in parallel at the falling edge of SEN. After the first row has been retrieved, the partial sum starts to be computed. Meanwhile, the same process for the second row can be started, so and so forth. To avoid reading the previous state, the duration of PH1 is preferred to be comparable with the retention time of SMTJ, which limits the main frequency of the system (see details in Supplementary Note  11 ).

We compare our system with other state-of-art Ising solvers, including CMOS annealer (Intel Core i7 processor) 7 , quantum annealer (D-Wave 2000Q) 16 , 17 , CIM with FPGA 26 , memristor Hopfield neural networks (mem-HNN) 44 , and phase-transition nano-oscillators (PTNO) 28 in solving 4761-node TSP70, as shown in Table  1 . We use the experimental data for benchmarking from literature, and two kinds of SMTJs for comparison. One is our perpendicular anisotropy SMTJ device and the other is assuming recently reported in-plane anisotropy SMTJ with a retention time of 8 ns 45 , 46 . The major attributes are the main frequency (defined as 1/iteration time), power, time-to-solution as well as energy efficiency (defined as solutions per second per watt). As quantum computers, CIM, mem-HNN, and PTNO only demonstrated ~100-node max-cut problems, we estimate the time-to-solution for solving TSP70 by assuming that the algorithm and the total number of spins to find a near-optimal solution is the same as our work (details in Supplementary Note  13 ). Here, we set 80-spin Ising computer as a standard and fix the number of iterations of 400,000 for a good solution to TSP70. Only Ising computing parts are calculated for power consumption.

In Table  1 , although the main frequency of CPU is the highest among all candidates, the energy efficiency is lower than our SMTJ-based approach. This is due to the redundant logic and data transfer delay between the memory and PEs in a conventional von-Neumann architecture. The SMTJ-based approach currently outperforms the quantum annealer both in the power consumption as well as time to solution. The power of quantum annealer is huge which needs to be optimized further for real applications. CIM is another promising architecture with a fast speed and acceptable power consumption. Current CIM systems are proof-of-concept systems which are not at present optimized for energy efficiency. Mem-HNN has a relatively fast speed assuming the 180-nm CMOS technology. However, the required number of devices is large, which limits the integrated density. The PTNO approach uses capacitors or resistors to mimic spin coupling, whose main frequency would be limited by the system scale and parasitic effects. It is reported that the ideal main frequency would decrease from 500 to 87 MHz when the system scale increases from 8-node to 100-node 28 . Our SMTJ-based Ising computer outperforms other approaches with low power consumption with 0.64 mW (details in Supplementary Note  13 ).

We experimentally demonstrate perpendicular MTJs with a retention time of ~0.1 ms and solve TSP70 Ising problems at an energy efficiency of 39 solutions per second per watt. Furthermore, we simulate an Ising computer with 4 Kb SMTJs using 40 nm commercial CMOS technology. The simulated energy efficiency for solving TSP70 by using the same SMTJ can reach 68 solutions per second per watt. By using reported in-plane SMTJ 45 and advanced CMOS, the system could obtain the highest energy efficiency of \(5.4\times {10}^{3}\) , which shows several orders of magnitude improvement over other approaches. This result suggests that an SMTJ-based Ising computer can be a good candidate for solving dense Ising problems in a highly energy-efficient and fast way.

In summary, we have experimentally demonstrated an intrinsic all-to-all Ising computer based on 80 SMTJs, and solved 9-city TSP with the optimal solution. Furthermore, a compressing strategy based on CTSP and GP is proposed to experimentally solve 4761-node 70-city TSP on an 80-node system with a near-optimum solution as well as ultra-low energy consumption. A cross-bar architecture is then proposed for large-scale Ising computers and the 200 city TSP task is simulated. Our system provides a feasible solution to fast, energy-efficient, and scalable Ising computing schemes to solve NP-hard problems.

Sample growth and device fabrication

Thin film samples of substrate/[W (3)/Ru (10)] 2 /W (3)/Pt (3)/Co (0.25)/Pt (0.2)/[Co (0.25)/Pt (0.5)] 5 /Co (0.6)/Ru (0.85)/Co (0.6)/Pt (0.2)/Co (0.3)/Pt (0.2)/Co (0.5)/W (0.3)/CoFeB (0.9)/MgO (1.1)/CoFeB (1.5)/Ta (3)/Ru (7)/Ta (5) were deposited via DC (metallic layers) and RF magnetron (MgO layer) sputtering on the Si substrates with thermal oxide of 300 nm with a base pressure of less than \(2\times {10}^{-8}\) Torr at room temperature. The numbers in parentheses are thicknesses in nanometers. To fabricate the superparamagnetic tunnel junctions, bottom electrode structures with a width of 10 µm were firstly patterned via photolithography and Ar ion milling. MTJ pillar structures with a diameter of ~50 nm for the superparamagnetic behavior were patterned by using e-beam lithography. The encapsulation layer of Si 3 N 4 was in-situ deposited after ion milling without breaking vacuum by using RF magnetron sputtering, and top electrode structures with a width of 10 µm were patterned via photolithography and top electrodes of Ta (5 nm)/Cu (40 nm) were deposited by using DC magnetron sputtering.

MTJ characterization by probe station

The setup includes a source meter (Keithley 2400) for supplying DC bias currents and a data acquisition card (NI-DAQmx USB-6363) for the read operation. A single SMTJ operation cycle comprises two steps (i.e. bias and read). A small DC input current with an amplitude of 1–20 μA is applied to SMTJ. Simultaneously, the DAQ card reads the voltage signal across the SMTJ at a maximum sampling rate of 2 MHz. The MTJ switching probability varies in accordance with the amplitude of applied currents. The retention time of MTJ is determined from random telegraph noise measurements over 250 ms. The expectation values of event time τ is determined by fitting an exponential function to the experimental results.

80 SMTJ arrays and peripheral circuits are integrated on a 12 cm × 15 cm PCB, controlled by an MCU (Arduino Mega 2560 Rev3). Four 12-bit rail-to-rail DACs (AD5381) with 160 output channels in total are used to generate analog DC inputs for PE and comparator arrays. Half of the DAC output channels are used to provide stimulation to the gate terminal of NMOSs (2N7002DW-G), and others are used to provide reference voltages to comparators (AD8694). The drain voltages of NMOS are compared with reference voltages and generate outputs in parallel. Outputs of comparator arrays are read by MCU through four multiplexers (FST16233) and then are calculated to obtain new inputs for DACs. The supply voltage of the PCB board and SMTJs is 5 V and 0.8 V, respectively. The value of resistors in each computing unit can be designed to adjust the center of sigmoidal curves.

Data availability

The data generated during this study are available within the article and the  Supplementary Information file.  Source data are provided with this paper.

Code availability

The codes that support this study can be available from the corresponding author upon request.

Theis, T. N. & Wong, H. S. P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 19 , 41–50 (2017).

Article   Google Scholar  

Shim, Y., Jaiswal, A. & Roy, K. Ising computation based combinatorial optimization using spin-Hall effect (SHE) induced stochastic magnetization reversal. J. Appl. Phys. 121 , 193902 (2017).

Article   ADS   Google Scholar  

Tindell, K. W., Burns, A. & Wellings, A. J. Allocating hard real-time tasks: An NP-Hard problem made easy. J. Real.-Time Syst. 4 , 145–165 (1992).

Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573 , 390–393 (2019).

Article   ADS   CAS   PubMed   Google Scholar  

Tatsumura, K., Hidaka, R., Yamasaki, M., Sakai, Y. & Goto, H. A Currency Arbitrage Machine Based on the Simulated Bifurcation Algorithm for Ultrafast Detection of Optimal Opportunity. in 2020 IEEE International Symposium on Circuits and Systems (ISCAS) 1–5 (IEEE, 2020). https://doi.org/10.1109/ISCAS45731.2020.9181114 .

Cohen, E., Carmi, M., Heiman, R., Hadar, O. & Cohen, A. Image restoration via ising theory and automatic noise estimation. In 2013 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB) 1–5 (IEEE, 2013). https://doi.org/10.1109/BMSB.2013.6621708 .

Zhou, A.-H. et al. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information 10 , 7 (2018).

Garza-Santisteban, F. et al. A Simulated Annealing Hyper-heuristic for Job Shop Scheduling Problems. In 2019 IEEE Congress on Evolutionary Computation (CEC) 57–64 (IEEE, 2019). https://doi.org/10.1109/CEC.2019.8790296 .

Lucas, A. Ising formulations of many NP problems. Front. Physics 2 , 5 (2014).

Albash, T. & Lidar, D. A. Adiabatic quantum computation. Rev. Mod. Phys. 90 , 015002 (2018).

Article   ADS   MathSciNet   Google Scholar  

Dickson, N. G. & Amin, M. H. S. Does Adiabatic Quantum Optimization Fail for NP-Complete Problems? Phys. Rev. Lett. 106 , 050502 (2011).

Article   ADS   PubMed   Google Scholar  

Heim, B., Ronnow, T. F., Isakov, S. V. & Troyer, M. Quantum versus classical annealing of Ising spin glasses. Science 348 , 215–217 (2015).

Article   ADS   MathSciNet   CAS   PubMed   Google Scholar  

Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58 , 5355–5363 (1998).

Article   ADS   CAS   Google Scholar  

Martoňák, R., Santoro, G. E. & Tosatti, E. Quantum annealing of the traveling-salesman problem. Phys. Rev. E 70 , 057701 (2004).

Okuyama, T., Hayashi, M. & Yamaoka, M. An Ising Computer Based on Simulated Quantum Annealing by Path Integral Monte Carlo Method. In 2017 IEEE International Conference on Rebooting Computing (ICRC) 1–6 (IEEE, 2017). https://doi.org/10.1109/ICRC.2017.8123652 .

Hamerly, R. et al. Experimental investigation of performance differences between Coherent Ising Machines and a quantum annealer. Sci. Adv. 5 , eaau0823 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473 , 194–198 (2011).

Yamaoka, M. et al. A 20k-Spin Ising Chip to Solve Combinatorial Optimization Problems With CMOS Annealing. IEEE J. Solid State Circuits 51 , 303–309 (2016).

Yamaoka, M. et al. 24.3 20k-spin Ising chip for combinational optimization problem with CMOS annealing. In 2015 IEEE International Solid-State Circuits Conference - (ISSCC) Digest of Technical Papers 1–3 (IEEE, 2015). https://doi.org/10.1109/ISSCC.2015.7063111 .

Davendra, D., Metlicka, M. & Bialic-Davendra, M. CUDA Accelerated 2-OPT Local Search for the Traveling Salesman Problem. In Novel Trends in the Traveling Salesman Problem (eds. Davendra, D. & Bialic-Davendra, M.) (IntechOpen, 2020). https://doi.org/10.5772/intechopen.93125 .

Tatsumura, K., Dixon, A. R. & Goto, H. FPGA-Based Simulated Bifurcation Machine. In 2019 29th International Conference on Field Programmable Logic and Applications (FPL) 59–66 (IEEE, 2019). https://doi.org/10.1109/FPL.2019.00019 .

Tatsumura, K., Yamasaki, M. & Goto, H. Scaling out Ising machines using a multi-chip architecture for simulated bifurcation. Nat. Electron 4 , 208–217 (2021).

Mathew, S. K. et al. μ RNG: A 300–950 mV, 323 Gbps/W All-Digital Full-Entropy True Random Number Generator in 14 nm FinFET CMOS. IEEE J. Solid-State Circuits 51 , 1695–1704 (2016).

Pervaiz, A. Z., Sutton, B. M., Ghantasala, L. A. & Camsari, K. Y. Weighted p-Bits for FPGA Implementation of Probabilistic Circuits. IEEE Trans. Neural Netw. Learn. Syst. 30 , 1920–1926 (2019).

Article   PubMed   Google Scholar  

McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354 , 614–617 (2016).

Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354 , 603–606 (2016).

Sutton, B., Camsari, K. Y., Behin-Aein, B. & Datta, S. Intrinsic optimization using stochastic nanomagnets. Sci. Rep. 7 , 44370 (2017).

Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron 4 , 502–512 (2021).

Sharmin, S., Shim, Y. & Roy, K. Magnetoelectric oxide based stochastic spin device towards solving combinatorial optimization problems. Sci. Rep. 7 , 11276 (2017).

Faria, R., Camsari, K. Y. & Datta, S. Implementing Bayesian networks with embedded stochastic MRAM. AIP Adv. 8 , 045101 (2018).

Zand, R., Camsari, K. Y., Datta, S. & DeMara, R. F. Composable Probabilistic Inference Networks Using MRAM-based Stochastic Neurons. J. Emerg. Technol. Comput. Syst. 15 , 1–22 (2019).

Choi, V. Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process 7 , 193–209 (2008).

Article   MathSciNet   Google Scholar  

Sugie, Y. et al. Minor-embedding heuristics for large-scale annealing processors with sparse hardware graphs of up to 102,400 nodes. Soft Comput 25 , 1731–1749 (2021).

Cai, J., Macready, W. G. & Roy, A. A practical heuristic for finding graph minors. Preprint at http://arxiv.org/abs/1406.2741 (2014).

Chaves-O’Flynn, G. D., Wolf, G., Sun, J. Z. & Kent, A. D. Thermal Stability of Magnetic States in Circular Thin-Film Nanomagnets with Large Perpendicular Magnetic Anisotropy. Phys. Rev. Appl. 4 , 024010 (2015).

Mitra, D., Romeo, F. & Sangiovanni-Vincentelli, A. Convergence and finite-time behavior of simulated annealing. Adv. Appl. Probab. 18 , 747–771 (1986).

Mills, K., Ronagh, P. & Tamblyn, I. Finding the ground state of spin Hamiltonians with reinforcement learning. Nat. Mach. Intell. 2 , 509–517 (2020).

MP-TESTDATA - The TSPLIB Symmetric Traveling Salesman Problem Instances. http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ (2013).

Dan, A., Shimizu, R., Nishikawa, T., Bian, S. & Sato, T. Clustering Approach for Solving Traveling Salesman Problems via Ising Model Based Solver. In 2020 57th ACM/IEEE Design Automation Conference (DAC) 1–6 (IEEE, 2020). https://doi.org/10.1109/DAC18072.2020.9218695 .

Ezugwu, A. E.-S., Adewumi, A. O. & Frîncu, M. E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem. Expert Syst. Appl. 77 , 189–210 (2017).

Mohsen, A. M. Annealing Ant Colony Optimization with Mutation Operator for Solving TSP. Comput. Intell. Neurosci. 2016 , 1–13 (2016).

Wang, J., Ersoy, O. K., He, M. & Wang, F. Multi-offspring genetic algorithm and its application to the traveling salesman problem. Appl. Soft Comput. 43 , 415–423 (2016).

Talatchian, P. et al. Mutual control of stochastic switching for two electrically coupled superparamagnetic tunnel junctions. Phys. Rev. B 104 , 054427 (2021).

Cai, F. et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nat. Electron 3 , 409–418 (2020).

Hayakawa, K. et al. Nanosecond Random Telegraph Noise in In-Plane Magnetic Tunnel Junctions. Phys. Rev. Lett. 126 , 117202 (2021).

Safranski, C. et al. Demonstration of Nanosecond Operation in Stochastic Magnetic Tunnel Junctions. Nano Lett. 21 , 2040–2045 (2021).

Download references

Acknowledgements

This work was supported by National Research Foundation (NRF), Prime Minister’s Office, Singapore, under its Competitive Research Programme (NRF-000214-00 to H.Y.), Advanced Research and Technology Innovation Center (ARTIC to H.Y.), the National University of Singapore under Grant (project number: A-0005947-19-00 to H.Y.), and Ministry of Education, Singapore, under Tier 2 (T2EP50123-0025 to H.Y.). We thank Yuqi Su, and Chne-Wuen Tsai from National University of Singapore and Zhi-Da Song from Peking University for useful discussions.

Author information

Authors and affiliations.

Department of Electrical and Computer Engineering, National University of Singapore, Singapore, Singapore

Jia Si, Shuhan Yang, Yunuo Cen, Jiaer Chen, Yingna Huang, Zhaoyang Yao, Dong-Jun Kim, Kaiming Cai, Jerald Yoo, Xuanyao Fong & Hyunsoo Yang

Key Laboratory for the Physics and Chemistry of Nanodevices and Center for Carbon-based Electronics, School of Electronics, Peking University, Beijing, China

You can also search for this author in PubMed   Google Scholar

Contributions

J.S. and H.Y. conceived and designed the experiments. J.S. designed, fabricated, and coded the hardware system. D.K., and S.Y. fabricated the devices. J.S., S.Y., and K.C. performed device measurements. Z.Y. bonded the components on PCB. J.S. designed SMTJ-based Ising system. J.S., J.C., Y.C., Y.H. and X.F. developed the optimization algorithm and performed simulations. J.S., S.Y., Y.C., J.Y., X.F. and H.Y. analyzed the data. J.S. and H.Y. wrote the manuscript. H.Y. proposed and supervised this work. All authors discussed the results and revised the manuscript.

Corresponding author

Correspondence to Hyunsoo Yang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information, source data, source data, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Si, J., Yang, S., Cen, Y. et al. Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems. Nat Commun 15 , 3457 (2024). https://doi.org/10.1038/s41467-024-47818-z

Download citation

Received : 16 June 2022

Accepted : 11 April 2024

Published : 24 April 2024

DOI : https://doi.org/10.1038/s41467-024-47818-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.