eulerian tour algorithm

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Graph Data Structure And Algorithms
• Introduction to Graphs - Data Structure and Algorithm Tutorials
• Graph and its representations
• Types of Graphs with Examples
• Basic Properties of a Graph
• Applications, Advantages and Disadvantages of Graph
• Transpose graph
• Difference Between Graph and Tree

BFS and DFS on Graph

• Breadth First Search or BFS for a Graph
• Depth First Search or DFS for a Graph
• Applications, Advantages and Disadvantages of Depth First Search (DFS)
• Applications, Advantages and Disadvantages of Breadth First Search (BFS)
• Iterative Depth First Traversal of Graph
• BFS for Disconnected Graph
• Transitive Closure of a Graph using DFS
• Difference between BFS and DFS

Cycle in a Graph

• Detect Cycle in a Directed Graph
• Detect cycle in an undirected graph
• Detect Cycle in a directed graph using colors
• Detect a negative cycle in a Graph | (Bellman Ford)
• Cycles of length n in an undirected and connected graph
• Detecting negative cycle using Floyd Warshall
• Clone a Directed Acyclic Graph

Shortest Paths in Graph

• How to find Shortest Paths from Source to all Vertices using Dijkstra's Algorithm
• Bellman–Ford Algorithm
• Floyd Warshall Algorithm
• Johnson's algorithm for All-pairs shortest paths
• Shortest Path in Directed Acyclic Graph
• Multistage Graph (Shortest Path)
• Shortest path in an unweighted graph
• Karp's minimum mean (or average) weight cycle algorithm
• 0-1 BFS (Shortest Path in a Binary Weight Graph)
• Find minimum weight cycle in an undirected graph

Minimum Spanning Tree in Graph

• Kruskal’s Minimum Spanning Tree (MST) Algorithm
• Difference between Prim's and Kruskal's algorithm for MST
• Applications of Minimum Spanning Tree
• Total number of Spanning Trees in a Graph
• Minimum Product Spanning Tree
• Reverse Delete Algorithm for Minimum Spanning Tree

Topological Sorting in Graph

• Topological Sorting
• All Topological Sorts of a Directed Acyclic Graph
• Kahn's algorithm for Topological Sorting
• Maximum edges that can be added to DAG so that it remains DAG
• Longest Path in a Directed Acyclic Graph
• Topological Sort of a graph using departure time of vertex

Connectivity of Graph

• Articulation Points (or Cut Vertices) in a Graph
• Biconnected Components
• Bridges in a graph
• Eulerian path and circuit for undirected graph
• Fleury's Algorithm for printing Eulerian Path or Circuit
• Strongly Connected Components
• Count all possible walks from a source to a destination with exactly k edges
• Euler Circuit in a Directed Graph
• Word Ladder (Length of shortest chain to reach a target word)
• Find if an array of strings can be chained to form a circle | Set 1
• Tarjan's Algorithm to find Strongly Connected Components
• Paths to travel each nodes using each edge (Seven Bridges of Königsberg)
• Dynamic Connectivity | Set 1 (Incremental)

Maximum flow in a Graph

• Max Flow Problem Introduction
• Ford-Fulkerson Algorithm for Maximum Flow Problem
• Find maximum number of edge disjoint paths between two vertices
• Find minimum s-t cut in a flow network
• Maximum Bipartite Matching
• Channel Assignment Problem
• Introduction to Push Relabel Algorithm
• Introduction and implementation of Karger's algorithm for Minimum Cut
• Dinic's algorithm for Maximum Flow

Some must do problems on Graph

• Find size of the largest region in Boolean Matrix
• Count number of trees in a forest
• A Peterson Graph Problem
• Clone an Undirected Graph
• Introduction to Graph Coloring
• Traveling Salesman Problem (TSP) Implementation
• Introduction and Approximate Solution for Vertex Cover Problem
• Erdos Renyl Model (for generating Random Graphs)
• Chinese Postman or Route Inspection | Set 1 (introduction)
• Hierholzer's Algorithm for directed graph
• Boggle (Find all possible words in a board of characters) | Set 1
• Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)
• Construct a graph from given degrees of all vertices
• Determine whether a universal sink exists in a directed graph
• Number of sink nodes in a graph
• Two Clique Problem (Check if Graph can be divided in two Cliques)

Fleury’s Algorithm for printing Eulerian Path or Circuit

Eulerian Path  is a path in a graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path that starts and ends on the same vertex.

We strongly recommend first reading the following post on Euler Path and Circuit. “ https://www.geeksforgeeks.org/eulerian-path-and-circuit/”

In the above-mentioned post, we discussed the problem of finding out whether a given graph is Eulerian or not. In this post, an algorithm to print an Eulerian trail or circuit is discussed.

Following is Fleury’s Algorithm for printing the Eulerian trail or cycle  Make sure the graph has either 0 or 2 odd vertices. If there are 0 odd vertices, start anywhere. If there are 2 odd vertices, start at one of them. Follow edges one at a time. If you have a choice between a bridge and a non-bridge, always choose the non-bridge . Stop when you run out of edges.

The idea is, “don’t burn bridges “ so that we can come back to a vertex and traverse the remaining edges. For example, let us consider the following graph.   

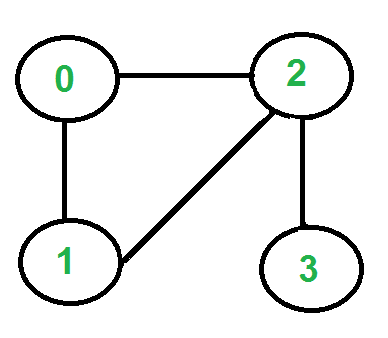
There are two vertices with odd degrees, ‘2’ and ‘3’, and we can start paths from any of them. Let us start the tour from vertex ‘2’.   

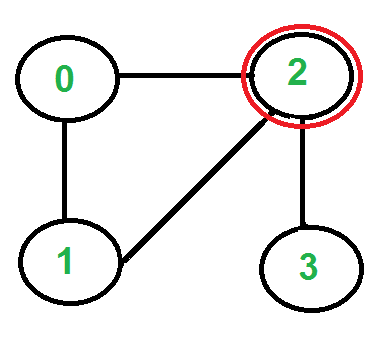
Three edges are going out from vertex ‘2’, which one to pick? We don’t pick the edge ‘2-3’ because that is a bridge (we won’t be able to come back to ‘3’). We can pick any of the remaining two edges. Let us say we pick ‘2-0’. We remove this edge and move to vertex ‘0’.   

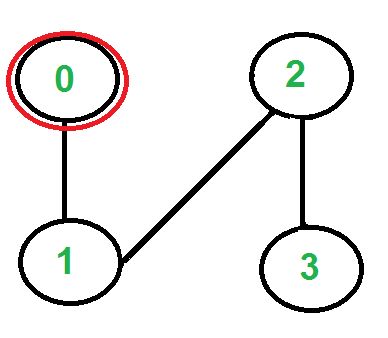
There is only one edge from vertex ‘0’, so we pick it, remove it and move to vertex ‘1’. Euler tour becomes ‘2-0 0-1’.   

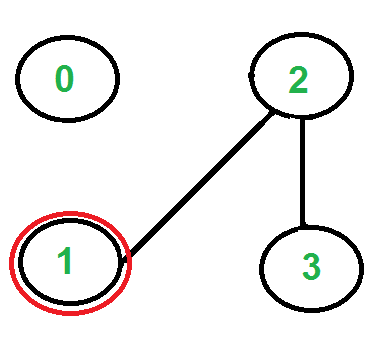
There is only one edge from vertex ‘1’, so we pick it, remove it and move to vertex ‘2’. Euler tour becomes ‘2-0 0-1 1-2’   

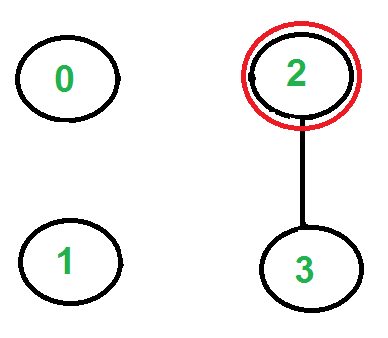
Again there is only one edge from vertex 2, so we pick it, remove it and move to vertex 3. Euler tour becomes ‘2-0 0-1 1-2 2-3’   

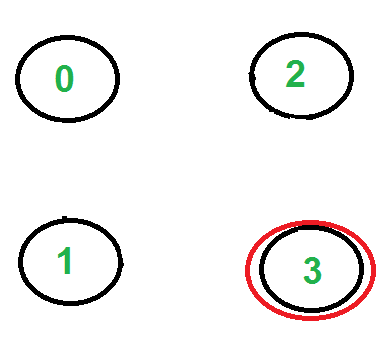
There are no more edges left, so we stop here. Final tour is ‘2-0 0-1 1-2 2-3’.

Following is the C++ implementation of the above algorithm. In the following code, it is assumed that the given graph has an Eulerian trail or Circuit. The main focus is to print an Eulerian trail or circuit. We can use isEulerian() to first check whether there is an Eulerian Trail or Circuit in the given graph. 

We first find the starting point which must be an odd vertex (if there are odd vertices) and store it in variable ‘u’. If there are zero odd vertices, we start from vertex ‘0’. We call printEulerUtil() to print Euler tour starting with u. We traverse all adjacent vertices of u, if there is only one adjacent vertex, we immediately consider it. If there are more than one adjacent vertices, we consider an adjacent v only if edge u-v is not a bridge. How to find if a given edge is a bridge? We count several vertices reachable from u. We remove edge u-v and again count the number of reachable vertices from u. If the number of reachable vertices is reduced, then edge u-v is a bridge. To count reachable vertices, we can either use BFS or DFS, we have used DFS in the above code. The function DFSCount(u) returns several vertices reachable from u. 

Once an edge is processed (included in the Euler tour), we remove it from the graph. To remove the edge, we replace the vertex entry with -1 in the adjacency list. Note that simply deleting the node may not work as the code is recursive and a parent call may be in the middle of the adjacency list.

Note that the above code modifies the given graph, we can create a copy of the graph if we don’t want the given graph to be modified.

Time Complexity: The time complexity of the above implementation is O ((V+E) 2 ). The function printEulerUtil() is like DFS and it calls isValidNextEdge() which also does DFS two times. The time complexity of DFS for adjacency list representation is O(V+E). Therefore overall time complexity is O((V+E)*(V+E)) which can be written as O(E 2 ) for a connected graph.  There are better algorithms to print Euler tour, Hierholzer’s Algorithm finds in O(V+E) time. Space complexity: O(V+E), the space complexity of the above program is O(V+E) as we are using an adjacency list to represent the graph. The size of the adjacency list is equal to the number of vertices plus the number of edges in the graph.

Please Login to comment...

Similar reads.

• Euler-Circuit

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Finding the Eulerian path in $O(M)$ ¶

A Eulerian path is a path in a graph that passes through all of its edges exactly once. A Eulerian cycle is a Eulerian path that is a cycle.

The problem is to find the Eulerian path in an undirected multigraph with loops .

Algorithm ¶

First we can check if there is an Eulerian path. We can use the following theorem. An Eulerian cycle exists if and only if the degrees of all vertices are even. And an Eulerian path exists if and only if the number of vertices with odd degrees is two (or zero, in the case of the existence of a Eulerian cycle). In addition, of course, the graph must be sufficiently connected (i.e., if you remove all isolated vertices from it, you should get a connected graph).

To find the Eulerian path / Eulerian cycle we can use the following strategy: We find all simple cycles and combine them into one - this will be the Eulerian cycle. If the graph is such that the Eulerian path is not a cycle, then add the missing edge, find the Eulerian cycle, then remove the extra edge.

Looking for all cycles and combining them can be done with a simple recursive procedure:

The complexity of this algorithm is obviously linear with respect to the number of edges.

But we can write the same algorithm in the non-recursive version:

It is easy to check the equivalence of these two forms of the algorithm. However, the second form is obviously faster, and the code will be much more efficient.

The Domino problem ¶

We give here a classical Eulerian cycle problem - the Domino problem.

There are $N$ dominoes, as it is known, on both ends of the Domino one number is written(usually from 1 to 6, but in our case it is not important). You want to put all the dominoes in a row so that the numbers on any two adjacent dominoes, written on their common side, coincide. Dominoes are allowed to turn.

Reformulate the problem. Let the numbers written on the bottoms be the vertices of the graph, and the dominoes be the edges of this graph (each Domino with numbers $(a,b)$ are the edges $(a,b)$ and $(b, a)$ ). Then our problem is reduced to the problem of finding the Eulerian path in this graph.

Implementation ¶

The program below searches for and outputs a Eulerian loop or path in a graph, or outputs $-1$ if it does not exist.

First, the program checks the degree of vertices: if there are no vertices with an odd degree, then the graph has an Euler cycle, if there are $2$ vertices with an odd degree, then in the graph there is only an Euler path (but no Euler cycle), if there are more than $2$ such vertices, then in the graph there is no Euler cycle or Euler path. To find the Euler path (not a cycle), let's do this: if $V1$ and $V2$ are two vertices of odd degree, then just add an edge $(V1, V2)$ , in the resulting graph we find the Euler cycle (it will obviously exist), and then remove the "fictitious" edge $(V1, V2)$ from the answer. We will look for the Euler cycle exactly as described above (non-recursive version), and at the same time at the end of this algorithm we will check whether the graph was connected or not (if the graph was not connected, then at the end of the algorithm some edges will remain in the graph, and in this case we need to print $-1$ ). Finally, the program takes into account that there can be isolated vertices in the graph.

Notice that we use an adjacency matrix in this problem. Also this implementation handles finding the next with brute-force, which requires to iterate over the complete row in the matrix over and over. A better way would be to store the graph as an adjacency list, and remove edges in $O(1)$ and mark the reversed edges in separate list. This way we can archive a $O(N)$ algorithm.

Practice problems: ¶

• CSES : Mail Delivery
• CSES : Teleporters Path
• singamandeep (88.48%)
• anishagg17 (3.03%)
• adamant-pwn (2.42%)
• jakobkogler (1.21%)
• svaderia (1.21%)
• Aryamn (1.21%)
• beingnoble03 (0.61%)
• sohaibuddinsyed (0.61%)
• apupneja (0.61%)
• algmyr (0.61%)

• 1 Definitions
• 2 Necessary and sufficient conditions
• 3 Fleury's algorithm
• 4.1 Pseudocode
• 5 Generalizations
• 6 Python implementation

Definitions [ edit ]

An Euler tour (or Eulerian tour) in an undirected graph is a tour that traverses each edge of the graph exactly once. Graphs that have an Euler tour are called Eulerian .

Some authors use the term "Euler tour" only for closed Euler tours.

Necessary and sufficient conditions [ edit ]

An undirected graph has a closed Euler tour iff it is connected and each vertex has an even degree.

An undirected graph has an open Euler tour (Euler path) if it is connected, and each vertex, except for exactly two vertices, has an even degree. The two vertices of odd degree have to be the endpoints of the tour.

A directed graph has a closed Euler tour iff it is strongly connected and the in-degree of each vertex is equal to its out-degree.

Similarly, a directed graph has an open Euler tour (Euler path) iff for each vertex the difference between its in-degree and out-degree is 0, except for two vertices, where one has difference +1 (the start of the tour) and the other has difference -1 (the end of the tour) and, if you add an edge from the end to the start, the graph is strongly connected.

Fleury's algorithm [ edit ]

Fleury's algorithm is a straightforward algorithm for finding Eulerian paths/tours. It proceeds by repeatedly removing edges from the graph in such way, that the graph remains Eulerian. A version of the algorithm, which finds Euler tour in undirected graphs follows.

Start with any vertex of non-zero degree. Choose any edge leaving this vertex, which is not a bridge (i.e. its removal will not disconnect the graph into two or more disjoint connected components). If there is no such edge, stop. Otherwise, append the edge to the Euler tour, remove it from the graph, and repeat the process starting with the other endpoint of this edge.

Though the algorithm is quite simple, it is not often used, because it needs to identify bridges in the graph (which is not a trivial thing to code.) Slightly more sophisticated, but easily implementable algorithm is presented below.

Cycle finding algorithm [ edit ]

This algorithm is based on the following observation: if C is any cycle in a Eulerian graph, then after removing the edges of C, the remaining connected components will also be Eulerian graphs.

The algorithm consists in finding a cycle in the graph, removing its edges and repeating this steps with each remaining connected component. It has a very compact code with recursion:

Pseudocode [ edit ]

This algorithm can also be used to find Eulerian paths: simply connect the path's endpoints by a dummy edge, and find Euler tour.

Generalizations [ edit ]

In some practical situations, it is desirable to find a cycle, which visits all edges of a graph, when the graph does not have an Euler tour. In this case some of the edges will have to be visited more than once. If the graph is weighted, and a minimum-cost such cycle is sought, then this is what is known as a Chinese Postman Problem .

It's possible to generalize Euler tours to the case of mixed graphs, which contain both directed and undirected edges. See article UVa_10735 for a description of one possible algorithm for such graphs.

Python implementation [ edit ]

This is a short implementation of the Euler tour in python.

• Graph Theory

Navigation menu

Reset password New user? Sign up

Existing user? Log in

Eulerian Path

Already have an account? Log in here.

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once, and the study of these paths came up in their relation to problems studied by Euler in the 18th century like the one below:

Is there a walking path that stays inside the picture and crosses each of the bridges exactly once?

After trying and failing to draw such a path, it might seem plausible that the task is impossible. But how can this be proven? What if the configuration of bridges is slightly different? (For instance, it is not hard to cross all but one of the bridges, and adding another bridge to the existing seven would also allow a complete crossing.) Is there a way to characterize the configurations that allow for these paths? What if the path is required to start and end at the same place?

The answers to these questions were first supplied in 1736, by Leonhard Euler , in a paper that proved the first result in what is now known as graph theory . Paths traversing all the bridges (or, in more generality, paths traversing all the edges of the underlying graph) are known as Eulerian paths , and Eulerian paths which start and end at the same place are called Eulerian circuits .

The problem above is known as the Bridges of Konigsberg problem, named after a city in Prussia on the Pregel River with bridges configured as in the picture.

An informal proof

Graphs, eulerian paths, and eulerian circuits, fleury's algorithm, proof of the theorem, bridges of konigsberg revisited, five-room puzzle.

There are four landmasses in the picture. Every path that crosses the bridges will go back and forth between these four landmasses. Suppose there is a person standing on each landmass and watching someone walking the path, counting every time the walker either enters or exits the landmass (including the beginning and end of the path in their count). If there is a path that crosses each bridge exactly once, what will the counters' numbers be when the walker finishes?

The counter on the top will have \( 3 \), since each of the three bridges that hits his landmass will have been crossed exactly once, and each crossing will be counted as either an entry or an exit. Similarly, the counter on the middle island will show \( 5 \), the counter on the right will show \( 3\), and the counter at the bottom will show \( 3 \).

But the walker enters and exits each landmass every time he passes through, which contributes \( 2 \) to the count, so each counter's final count should be an even number--except for the two counters who count the beginning and the end of the path (the first exit doesn't have a corresponding entry, and the last entry doesn't have a corresponding exit). Still, it's impossible for all four counters to end with odd numbers, so there is no such path.

This problem can be rephrased in terms of graph theory , as follows. Consider the graph with vertices corresponding to the four landmasses, and edges between the vertices corresponding to the bridges. The path in question is a traversal of the graph that passes through each edge exactly once. Or, in other words, it is a drawing of the graph on a piece of paper without picking up our pencil or drawing any edge more than once.

In what follows, graphs will be assumed to be finite (with finitely many vertices and edges). Recall that the degree of a vertex in a graph is the number of edges that touch the vertex.

Here is the graph that corresponds to the bridge problem.

The degree of a vertex corresponding to one of the four landmasses in the original problem is the number that each counter will have in the above proof: the top, right, and bottom vertices have degree \( 3 \) and the left vertex has degree \( 5 \).

An Eulerian path on a graph is a traversal of the graph that passes through each edge exactly once. It is an Eulerian circuit if it starts and ends at the same vertex. \(_\square\)

The informal proof in the previous section, translated into the language of graph theory, shows immediately that:

If a graph admits an Eulerian path, then there are either \( 0 \) or \( 2 \) vertices with odd degree. If a graph admits an Eulerian circuit, then there are \( 0 \) vertices with odd degree.

The more interesting and difficult statement is the converse. What conditions guarantee the existence of an Eulerian path or Eulerian circuit? It turns out that aside from the necessary conditions on degrees, the only other requirement is the obvious one that any two vertices of degree \(\ge 1\) have a path between them.

A graph is connected if there is a path between any two vertices. \(_\square\)

Every (finite) graph can be uniquely decomposed into connected components : each component is a connected subgraph, and there are no edges between any two components. A vertex of degree zero is its own connected component.

A graph has an Eulerian path if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) there are 0 or 2 vertices of odd degree. A graph has an Eulerian circuit if and only if (1) every vertex of degree \(\ge 1\) lies in the same connected component, and (2) every vertex has even degree. \(_\square\)

Euler stated this theorem without proof when he solved the Bridges of Konigsberg problem in 1736, but the proof was not given until the late \(19^\text{th}\) century.

Can we color the edges of the octahedron above without lifting the pencil nor coloring the same edge more than once?

Define the cube graph \( C_n \) as follows:

There are \( 2^n \) vertices, labelled \( v_0, v_1, \ldots, v_{2^n-1} \). Draw an edge between \( v_a \) and \( v_b\) if and only if the binary representations of \( a \) and \( b\) differ in exactly one digit.

We would like to find a path along the cube graph \( C_n \) that crosses each edge exactly once, and begins and ends at the same vertex. For \( C_2 \) this is possible: start at 0, move to 2, move to 3, move to 1, move back to 0.

What about for \( n = 3 \) or \( n = 4 ? \)

To prove the theorem, the "only if" statements have been established by the above discussion. One way to prove the "if" statements is via the following algorithm due to Fleury which constructs an Eulerian path or circuit.

If there are two vertices of odd degree, start with one of them. Otherwise, start with any vertex. At every step of the algorithm, pick an edge that will not disconnect the graph if it is removed, unless there is no such edge. (Edges that will disconnect the graph if they are removed are--somewhat confusingly in this context--called bridges .) Move along this edge and delete it from the graph once done. Continue.

Every graph has an even number of vertices with odd degree.

Proof: Every edge hits two vertices, so the sum of the degrees of the vertices equals twice the number of edges. So it is even. The lemma follows immediately.

Rather than giving the details of this proof, here is an alternative algorithm due to Hierholzer that also works. The algorithm produces Eulerian circuits, but it can be modified to produce Eulerian paths if there are two vertices of odd degree.

Suppose every vertex has even degree. Start with a vertex \( v \) and follow a path around the graph until it returns to \( v\). This will always be possible because there will always be an odd number of unused edges emanating from a vertex that the path has landed on. This produces a circuit that may not be Eulerian; but if it is not, we can start from a vertex \(w\) with some unused edges coming from it and follow a path of unused edges around the graph until it returns to \( w \). The old circuit plus the new one can be traversed as one large circuit (start at \( v\), go to \( w\), do the \( w\) circuit, continue the rest of the \( v\) circuit). Repeat until there are no more unused edges. \( \square\)

A graph in which all vertices have even degree. [1] Consider the above graph. Starting at vertex 1, draw a circuit 1-2-3-7-1. There are unused edges emanating from vertex 1, so draw another circuit 1-3-4-7-8-1. Put them together to get 1-2-3-7-1-3-4-7-8-1. Now vertex 1 no longer has unused edges, but vertex 4 does: draw 4-5-9-4. Stick this into the previous circuit to get \[ 1-2-3-7-1-3-{\bf 4-5-9-4}-7-8-1. \] Finally, vertex 9 has some unused edges left, so draw the circuit 9-6-7-9 and notice that all the edges have been used. Stick it into the previous circuit to get \[ 1-2-3-7-1-3-4-5-{\bf 9-6-7-9}-4-7-8-1. \]

The Konigsberg bridges have the interesting property that adding or deleting a bridge between any two landmasses will allow an Eulerian path. Indeed, adding or deleting a bridge will change the parity of the degrees of two of the four vertices of the associated graph, which will make them both even. Then there will be two vertices of odd degree, which will imply the existence of an Eulerian path.

This illustrates the power of the theorem; without having to draw the paths in all of the various cases that might arise, nevertheless an affirmative answer can be given to the question of the existence of Eulerian paths.

Another application of the theorem is to the following puzzle:

Suppose five rooms in a house are laid out as follows: Imagine a door cut into each wall of each room (including the outside). Is there a path that goes through each door exactly once? The answer is no, as the associated graph has four vertices of odd degree. Here are the graphs for the Konigsberg and five-room problems, respectively, with degrees pictured on each vertex. Note that it is possible in the five-room problem to construct a path that passes through all but one door, but in this case only certain doors can be omitted; the door has to correspond to an edge connecting two odd-degree vertices. \(_\square\)

• Tin Tin, C. Hierholzer's algorithm . Retrieved August 8, 2008, from https://commons.wikimedia.org/wiki/File:Hierholzer_(3).png

Problem Loading...

Note Loading...

Set Loading...

Search anything:

Fleury’s Algorithm: Finding Eulerian tours in a graph

Graph algorithms depth first search fleury algorithm.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Applications

• Discussions

Reading time: 10 minutes | Coding time: 12 minutes

Fleury's algorithm is a simple algorithm for finding Eulerian paths or tours. It proceeds by repeatedly removing edges from the graph in such way, that the graph remains Eulerian.

The steps of Fleury's algorithm is as follows:

• Start with any vertex of non-zero degree.
• Choose any edge leaving this vertex, which is not a bridge (cut edges).
• If there is no such edge, stop.
• Otherwise, append the edge to the Euler tour, remove it from the graph, and repeat the process starting with the other endpoint of this edge.
• Worst case time complexity: Θ((V+E)^2)
• Average case time complexity: Θ((V+E)^2)
• Best case time complexity: Θ((V+E)^2)
• Space complexity: Θ(V^2)
• CodeForces: Strongly Connected City
• CodeForces: New Year Santa Network
• Find Eulerian path in a graph

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.1: Euler Tours and Trails

• Last updated
• Save as PDF
• Page ID 60138

• University of Lethbridge

To introduce these concepts, we need to know about some special kinds of walks.

Definition: Special Kinds of Works

• A walk is closed if it begins and ends with the same vertex.
• A trail is a walk in which no two vertices appear consecutively (in either order) more than once. (That is, no edge is used more than once.)
• A tour is a closed trail.
• An Euler trail is a trail in which every pair of adjacent vertices appear consecutively. (That is, every edge is used exactly once.)
• An Euler tour is a closed Euler trail.

Recall the historical example of the bridges of Königsberg. The problem of finding a route that crosses every bridge exactly once, is equivalent to finding an Euler trail in the corresponding graph. If we want the route to begin and end at the same place (for example, someone’s home), then the problem is equivalent to finding an Euler tour in the corresponding graph.

Euler tours and trails are important tools for planning routes for tasks like garbage collection, street sweeping, and searches.

Example \(\PageIndex{1}\)

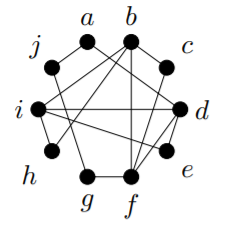
In the graph

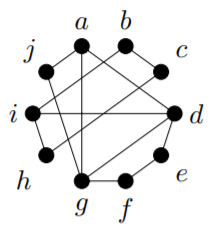
\((i, b, c, h, i, d, e, f, g, d, a, g, j, a)\) is an Euler trail. In the graph

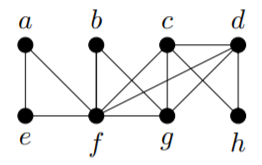
\((a, e, f, b, g, f, c, d, h, c, g, d, f, a)\) is an Euler tour.

Here is Euler’s method for finding Euler tours. We will state it for multigraphs, as that makes the corresponding result about Euler trails a very easy corollary.

Theorem \(\PageIndex{1}\)

A connected graph (or multigraph, with or without loops) has an Euler tour if and only if every vertex in the graph has even valency.

As the statement is if and only if, we must prove both implications.

\((⇒) Suppose we have a multigraph (possibly with loops) that has an Euler tour,

\[(u_1, u_2, . . . , u_{e+1} = u_1),\]

where \(e = |E|\). Let \(u\) be an arbitrary vertex of the multigraph. Every time \(u\) appears in the tour, exactly two of the edges incident with \(u\) are used: if \(u = u_j\), then the edges used are \(u_{j−1}u_j\) and \(u_ju_{j−1}\) unless \(j = 1\) or \(j = e + 1\) in which case \(u = u_1 = u_{e+1}\) and the edges are \(u_eu\) and \(uu_2\) (and we consider this as one appearance of u in the tour). Therefore, if \(u\) appears \(k\) times in the tour, then since by the definition of an Euler tour all edges incident with \(u\) are used exactly once, we conclude that \(u\) must have valency \(2k\). Since \(u\) was an arbitrary vertex of the multigraph and \(k\) (the number of times \(u\) appears in the tour) must be an integer, this shows that the valency of every vertex must be even.

\((⇐)\) Suppose we have a connected multigraph in which the valency of every vertex is even. Consider the following algorithm (which will be the first stage of our final algorithm):

Make \(u\) (some arbitrary vertex) our active vertex, with a list \(L\) of all of the edges of \(E\). Make \(u\) the first vertex in a new sequence \(C\) of vertices. Repeat the following step as many times as possible:

Call the active vertex \(v\). Choose any edge \(vx\) in \(L\) that is incident with \(v\). Add \(x\) (the other endvertex of this edge) to the end of \(C\), and make \(x\) the new active vertex. Remove \(vx\) from \(L\).

We claim that when this algorithm terminates, the sequence \(C\) will be a tour (though not necessarily an Euler tour) in the multigraph. By construction, \(C\) is a walk, and \(C\) cannot use any edge more than once since each edge appears in \(L\) only once and is removed from \(L\) once it has been used, so \(C\) is a trail. We need to show that the walk \(C\) is closed.

The only way the algorithm can terminate is if \(L\) contains no edge that is incident with the active vertex. Towards a contradiction, suppose that this happens at a time when the active vertex is \(y \neq u\). Now, \(y\) has valency \(2r\) in the multigraph for some integer \(r\), so there were \(2r\) edges in \(L\) that were incident with \(y\) when we started the algorithm. Since \(y \neq u\), every time \(y\) appears in \(C\) before this appearance, we removed \(2\) edges incident with \(y\) from \(L\) (one in the step when we made \(y\) the active vertex, and one in the following step). Furthermore, we removed one additional edge incident with \(y\) from \(L\) in the final step, when we made \(y\) the active vertex again. Thus if there are \(t\) previous appearances of \(y\) in \(C\), we have removed \(2t + 1\) edges incident with \(y\) from \(L\). Since \(2r\) is even and \(2t+ 1\) is odd, there must still be at least one edge incident with \(y\) that is in \(L\), contradicting the fact that the algorithm terminated. This contradiction shows that, when the algorithm terminates, the active vertex must be \(u\), so the sequence \(C\) is a closed walk. Since \(C\) is a trail, we see that \(C\) must be a tour.

If the tour \(C\) is not an Euler tour, let \(y\) be the first vertex that appears in \(C\) for which there remains an incident edge in \(L\). Repeat the previous algorithm starting with \(y\) being the active vertex, and with \(L\) starting at its current state (not all of \(E\)). The result will be a tour beginning and ending at y that uses only edges that were not in \(C\). Insert this tour into \(C\) as follows: if \(C = (u = u_1 . . . , y = u_i , . . . , u_k = u)\) and the new tour is \((y = v_1, . . . , v_j = y)\), then the result of inserting the new tour into \(C\) will be

\[(u = u_1, . . . , y = u_i = v_1, v_2, . . . , v_j = y = u_i , u_{i+1}, . . . , u_k = u).\]

Replace \(C\) by this extended tour.

Repeat the process described in the previous paragraph as many times as possible (this is the second and last stage of our final algorithm). Since \(E\) is finite and the multigraph is connected, sooner or later all of the edges of \(L\) must be exhausted. At this point, we must have an Euler tour.

Example \(\PageIndex{2}\)

Use the algorithm described in the proof of the previous result, to find an Euler tour in the following graph.

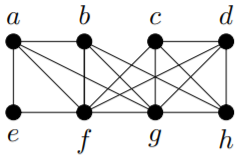
Let’s begin the algorithm at \(a\). As \(E = L\) is a large set, we won’t list the remaining elements every time we choose a new active vertex in the early stages. An easy method for you to keep track of the edges still in \(L\) is to colour the edges that are no longer in \(L\) (the edges we use) with a different colour as we go.

There are many different possible outcomes for the algorithm since there are often many acceptable choices for the next active vertex. One initial set of choices could be

\(C = (a, b, f, e, a, f, g, a).\)

The first stage of the algorithm terminates at this point since all four edges incident with \(a\) have been used. At this point, we have

\(L = \{bg, bh, cd, cf, cg, ch, df, dg, dh, gh\}.\)

The first vertex in \(C\) that is incident with an edge in \(L\) is \(b\). We run the first stage of the algorithm again with \(b\) as the initial active vertex and this list for \(L\). Again, there are many possible outcomes; one is \((b, g, h, b)\).

We insert \((b, g, h, b)\) into \(C\), obtaining a new \(C = (a, b, g, h, b, f, e, a, f, g, a)\). At this point, we have

\(L = \{cd, cf, cg, ch, df, dg, dh\}.\)

Now \(g\) is the first vertex in \(C\) that is incident with an edge in \(L\). We run the first stage of the algorithm again with \(g\) as the initial active vertex and the current \(L\). One possible outcome is \((g, c, f, d, g)\).

Inserting this into \(C\) yields a new

\(C = (a, b, g, c, f, d, g, h, b, f, e, a, f, g, a).\)

At this point, we have \(L = \{cd, ch, dh\}\). The first vertex in \(C\) that is incident with an edge in \(L\) is \(c\). We run the first stage of the algorithm one final time with \(c\) as the initial active vertex and \(L = \{cd, ch, dh\}\). This time there are only two possible outcomes: \((c, d, h, c)\) or \((c, h, d, c)\). We choose \((c, d, h, c)\).

Inserting this into \(C\) yields our Euler tour:

\(C = (a, b, g, c, d, h, c, f, d, g, h, b, f, e, a, f, g, a).\)

Corollary \(\PageIndex{1}\)

A connected graph (or multigraph, with or without loops) has an Euler trail if and only if at most two vertices have odd valency.

Suppose we have a connected graph (or multigraph, with or without loops), \(G\). Since the statement is if and only if, there are two implications to prove.

\((⇒)\) Suppose that \(G\) has an Euler trail. If the trail is closed then it is a tour, and by Theorem 13.1.1, there are no vertices of odd valency. If the trail is not closed, say it is a \(u − v\) walk. Add an edge between \(u\) and \(v\) to \(G\), creating a new graph \(G^∗\) (note that \(G^∗\) may be a multigraph if \(uv\) was already an edge of \(G\), even if \(G\) wasn’t a multigraph), and add \(u\) to the end of the Euler trail in \(G\), to create an Euler tour in \(G^∗\). By Theorem 13.1.1, the fact that \(G^∗\) has an Euler tour means that every vertex of \(G^∗\) has even valency. Now, the vertices of \(G\) all have the same valency in \(G^∗\) as they have in \(G\), with the exception that the valencies of \(u\) and \(v\) are one higher in \(G^∗\) than in \(G\). Therefore, in this case there are exactly two vertices of odd valency in \(G\); namely, \(u\) and \(v\).

\((⇐)\) Now we suppose that \(G\) has at most \(2\) vertices of odd valency. By Corollary 11.3.1 (the corollary to Euler’s handshaking lemma), if there are at most two vertices of odd valency, then there are either \(0\) or \(2\) vertices of odd valency. We consider these two cases.

If there are \(0\) vertices of odd valency, then by Theorem 13.1.1, \(G\) has an Euler tour.

If there are two vertices of odd valency, say \(u\) and \(v\), add an edge between \(u\) and \(v\) to \(G\), creating a new graph \(G^∗\) (note that \(G^∗\) may be a multigraph if \(uv\) was already an edge of \(G\), even if \(G\) wasn’t a multigraph). Now in \(G^∗\) every vertex has even valency, so \(G^∗\) has an Euler tour. In fact, a careful look at the algorithm given in the proof of Theorem 13.1.1 shows that we may choose \(u\) and \(v\) (in that order) to be the first two vertices in this Euler tour, so that \(uv\) (the edge that is in \(G^∗\) but not \(G\)) is the first edge used in the tour. Now if we delete \(u\) from the start of this Euler tour, the result is an Euler trail in \(G\) that starts at \(v\) and ends at \(u\).

Exercise \(\PageIndex{1}\)

For each of the following graphs, is there an Euler tour? Is there an Euler trail? If either exists, find one; if not, explain why not.

4) If it is possible, draw a graph that has an even number of vertices and an odd number of edges, that also has an Euler tour. If that isn’t possible, explain why there is no such graph.

5) Which complete graphs have an Euler tour? Of the complete graphs that do not have an Euler tour, which of them have an Euler trail?

Exercise \(\PageIndex{2}\)

Eulerian Cycle

An Eulerian cycle, also called an Eulerian circuit, Euler circuit, Eulerian tour, or Euler tour, is a trail which starts and ends at the same graph vertex . In other words, it is a graph cycle which uses each graph edge exactly once. For technical reasons, Eulerian cycles are mathematically easier to study than are Hamiltonian cycles . An Eulerian cycle for the octahedral graph is illustrated above.

As a generalization of the Königsberg bridge problem , Euler showed (without proof) that a connected graph has an Eulerian cycle iff it has no graph vertices of odd degree .

Fleury's algorithm is an elegant, but inefficient, method of generating an Eulerian cycle. An Eulerian cycle of a graph may be found in the Wolfram Language using FindEulerianCycle [ g ].

Explore with Wolfram|Alpha

More things to try:

• acyclic graph
• area between the curves y=1-x^2 and y=x

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Eulerian Cycle." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/EulerianCycle.html

Subject classifications